織物ミクロ構造の作成

織物材料のジオメトリ、ミクロ構造、および制限事項について詳細を確認します。

ジオメトリの生成

現在、Composite Material Manager では、5 種類のミクロ構造をサポートしています。最初の最も簡単なものは、母材材料に埋め込まれた繊維から構成される一方向複合材料です。残りの 4 つは、2 次元の織物ミクロ構造で構成されています。これには、平織物、4 枚朱子織物、5 枚朱子織物、8 枚朱子織物複合材料が含まれています。

どのミクロ構造でも、現実的なモデルを構築するためにジオメトリ パラメータが必要です。一方向材料の場合は、一方向複合材料の繊維体積分率(FVF)のみが必要です。FVF を使用して六角形の繊維充填配置を仮定し、マイクロメカニックス モデルのジオメトリが目的の複合材料用に作成されます。ただし、織物ジオメトリは 2 つの理由ではるかに複雑になります。

  1. 単位セルのジオメトリを説明するには、多くのパラメータが必要です。
  2. 平織物ジオメトリを説明するために使用される汎用データ セットはありません。

2 次元の織物材料には多様な組み合わせがあります。数例を挙げると、バランスの良好な平織物、アンバランスな平織物、綾織物、朱子織物などがあります。Helius PFA で使用される現在のモデルには、2 次元の平織物、4 枚、5 枚、8 枚朱子織物ミクロ構造が含まれます。綾織物などの直交けん引のみを含む、その他の織物構成に対して、平織物モデルは妥当な推定値を提供しますが、結果の精度に関する判断はユーザに委ねられます。したがって、一方向のクロスプライ積層(各層は個別のけん引方向を表す)として材料をモデリングすることによって、単層の材料特性の上限を計算することをお勧めします。三軸編み物などの非直交けん引のあるミクロ構造に対しては、現在、オートデスクではモデリング機能を提供していません。

次のセクションでは、Helius PFA に導入された織物ミクロ構造について説明し、織物材料の特性を適切に指定するために必要なパラメータの選択に関する情報を提供します。

平織物ミクロ構造

平織物複合材料マイクロメカニックス モデルは、充填けん引、反りけん引、母材ポケットから構成されています。充填けん引と反りけん引は、相互に垂直であると仮定されます。このタイプのミクロ構造をモデル化するために選択した単位セルは、Kuhn と Charalambides [1]から取得され、次のように表示されます。

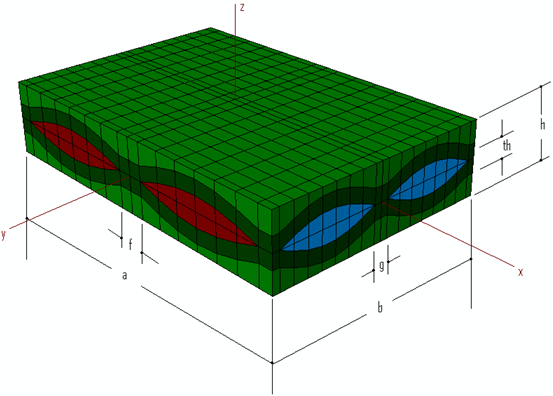
unit cell

上図に示すように、単位セルのジオメトリを完全に表現するために必要な多数のパラメータがあります。これらは次のとおりです。

  1. 単位セルの長さ
  2. 単位セルの幅
  3. 合計単位セルの高さ
  4. 充填けん引の高さ
  5. 反りけん引の高さ
  6. 充填けん引間の間隔
  7. 反りけん引間の間隔

母材ポケットなしの単位セルを次に表示します。

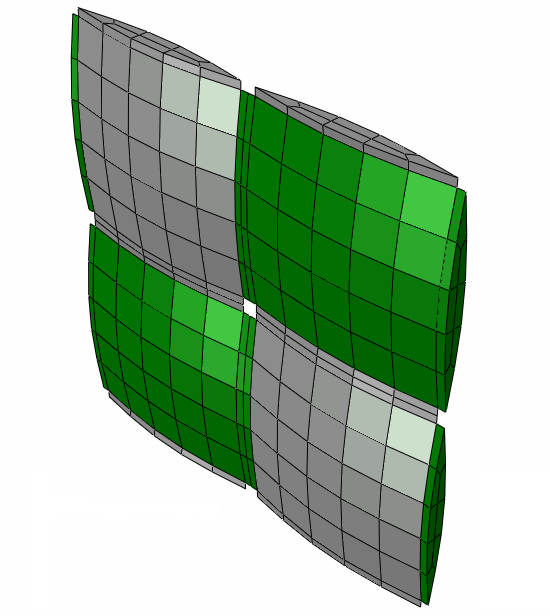
fill warp

縮小単位セル ミクロ構造(朱子織物)

朱子織り材料の縮小単位セル(RUC)ミクロ構造は、完全単位セル ミクロ構造を改良したものです。RUC は、FUC 内に見られる反復ジオメトリの単なるサブセットです。RUC では、n 枚朱子織物材料のミクロ構造を調整するのではなく、一定のサイズとトポロジが維持されます。朱子織り数が変化すると、中央にある 2 つのけん引の曲率の振幅のみが調整されます。

unit cell

ruc amplitude

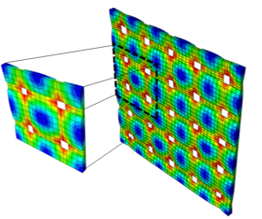
具体的には、平均面内剛性(E11、E22、G12)が、実験で観測された各朱子織り数の値と一致できるように、振幅が調整されます。

RUC ミクロ構造は FUC より小さく、したがって特性の決定がずっと高速になるという明確な利点を持ちます。そのため、RUC ミクロ構造では、繊維剛性および母材剛性の即座の劣化がサポートされています。また、FUC ではサポートされていない、破損前非線形性もサポートされています。

実験データの制限事項

繊維強化織物複合材料の実験データは、通常、複合材料全体の繊維体積分率のみを特性設定します。繊維強化一方向複合材料と同様に、これは複合材料の総体積に占める複合材料内の繊維の総体積の指標となります。これは、一方向材料ではうまく機能しますが、織物ミクロ構造のジオメトリをうまく表現できません。前述したパラメータに単位セルのジオメトリをリンクするには、1 つの基本的な質問に回答する必要があります。充填けん引と反りけん引の体積分率は何であるか?

この質問に回答するには、体積分率間の関係を作成する必要があります。複合材料の繊維の体積分率合計は、充填けん引と反りけん引の体積分率、およびそれぞれの繊維の体積分率で、次のように表すことができます。

FVF = BVFFill (FVFFill ) + BVFWarp (FVFWarp )、(方程式 1)

ここで、BVFFill は充填束体積分率、BVFWarp は反り束体積分率、FVFFill は充填けん引の繊維体積分率、FVFWarp は反りけん引の繊維体積分率です。束体積分率は、指定したけん引が複合材料全体に対して占める体積分率として定義されます。束体積分率や平織物単位セルのジオメトリの環境でそれが意味することについて、さらに詳細に説明します。下図をご覧ください。赤色でハイライト表示された領域は、複合材料セル単位内で充填けん引が占める体積を表します。充填束体積分率は、充填けん引体積を複合材料体積で除算して計算します。

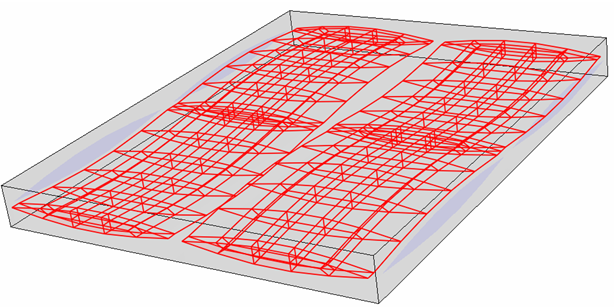
bundle vol

仮定

ここで、単位セルのジオメトリに関するいくつかの仮定を行います。最初に、充填けん引と反りけん引の高さが等しいと仮定し、どちらの高さへの依存性も除去します。2 番目の仮定は、任意のジオメトリ指定で、単位セルの高さ合計とけん引の高さを一定であると定義します。これにより、上記のリストの 3 番目、4 番目、5 番目の依存性が削除されます。

最後に、けん引の幅が等しく一定であると仮定します。これらにより、単位セルの幅および長さとけん引の間隔を、次のように関係付けることができます。

a = 幅 + 2f

b = 幅 + 2g、(方程式 2)

これで、単位セルのジオメトリを完全に説明するのに必要な不明のパラメータは、充填けん引間の間隔と反りけん引間の間隔の 2 つのみとなりました。これらのパラメータは、充填束と反り束の体積分率、および単位長あたりのうねり数と直接関係します。Composite Material Manager では、ミクロ構造を定義するために束体積分率(BVF)を使用します。

充填束と反り束の繊維体積分率は等しいと仮定します。よって、方程式 1 は次のように簡素化できます。

FVF = (BVFFill + BVFWarp )FVFTow、(方程式 3)

親ページ: 付録 E: 織物材料ファイルにジオメトリを指定するための追加情報