粘性材料で損傷が開始すると、材料の剛性が低減します(損傷の進展)。材料変形が継続して大きくなるにつれて、損傷は引き続き進展します。最終的に材料は完全に損傷したと見なされ、剛性はゼロになります。低減された材料剛性は、次のように示される損傷変数 D によって制御されます。

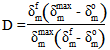
ここで、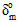 は損傷の開始時の有効な相対変位で、 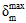は荷重履歴内で到達した有効な最大相対変位で、 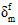は完全な破損時の有効な相対変位です。有効な相対変位は、次のように定義されます。

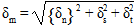
ここで、δn、δs、δt は、それぞれローカルの 3、1、2 方向の 3 つの相対変位です。次に、元の剛性値と次に示す損傷変数を使用して、表面力を計算します。

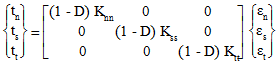
一般的な表面力変位曲線を下に示します。損傷は 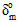(D=0)で開始し、損傷は 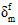(D=1)の点まで進展し続けます。

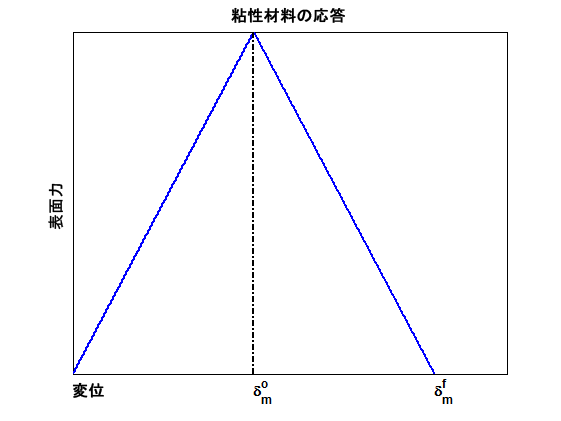
変位ベースの損傷の進展

変位ベースの損傷の進展基準では、引数 10 は、完全な破損時 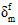の有効な相対変位と損傷の開始時 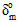の有効な相対変位の差として解釈されます。有効な値は 0 (ゼロ)より大きい必要があります。上記の図は 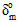および 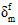と損傷の進展速度との定性的な関係を示しています。

エネルギー ベースの損傷の進展

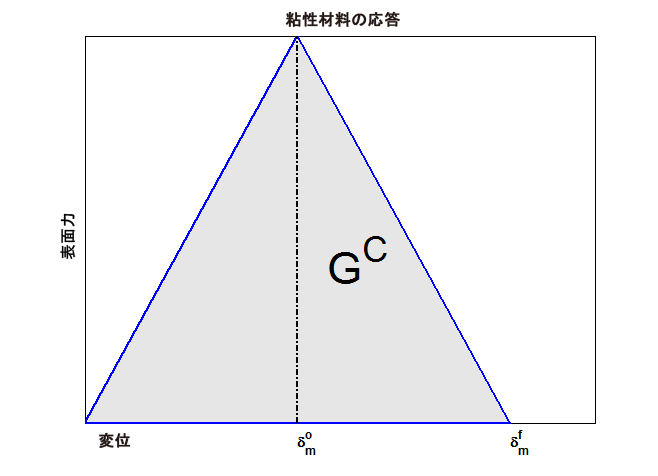
エネルギー ベースの損傷の進展基準では、引数 10 は、粘性材料の合計破断エネルギー、GC と解釈されます。 次の図は、GC と粘性材料の表面力-分離応答との関係を示しています。 指定された GC の値を使用して、次のように最終的な有効な相対変位を決定します。

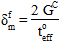
ここで、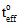 は損傷の開始時の有効な表面力です。

エネルギー ベースの損傷の進展(混合モード、べき乗則)

エネルギー ベースの混合モードべき乗則基準は、各荷重モードに対して破断エネルギーを使用して、損傷の進展を決定します。単一の破断エネルギー、GC の代わりに、各モードの破断エネルギー(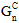、、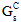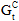)をそれぞれ引数 10、11、12 を使用して指定します。また、べき乗則で使用する指数、α を指定する必要があります。べき乗則は、次の条件が満たされた場合に、粘性材料が完全に破損したことを示します(D = 1)。

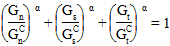
ここで、Gn、Gs、Gt は、表面力と ローカル 3、1、2 方向にある、それぞれに対応する相対変位による作用で引き起こされます。