付録 A.7: 損傷の進展方法(DEVO)

(エネルギー ベースの劣化は織物材料との互換性がありません)

DEVO フィールドの値が INSTANT の場合は、瞬間的な劣化が使用されます。EBD の場合は、エネルギー ベースの劣化が使用されます。

瞬間的な劣化

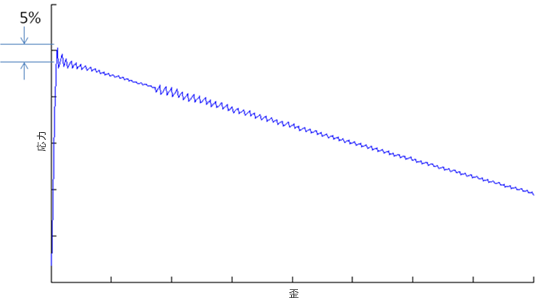
瞬間的な劣化は、Helius PFA によって使用される既定の損傷の進展方法です。損傷基準で破損が予測され、瞬間的な劣化が使用される場合、繊維または母材の剛性は段階的にではなく、瞬間的に最小値まで低減します。低減の大きさは、母材および繊維の劣化比率(MPSTIF と FPSTIF)によってコントロールされます。最大応力などの特定の破損基準は、母材と繊維を区別しないことに注意してください。これらの基準では、破損が予測されると複合材料の剛性は瞬間的に低減します。母材と繊維の剛性が個別に低減する場合とは対照的です。下記の図では、瞬間的な剛性低減の効果を説明するために、異なる破損状態における複合材料の剛性を示しています。複合材料の剛性は、母材破損が発生するまで一定を保ち、母材破損時に母材の剛性は元の剛性の任意の比率(MPSTIF)にまで低減します。母材の剛性低減は、複合材料の剛性低減に対応し、この低減は 1 度の増分で適用されます。繊維破損の発生時に、繊維の剛性は FPSTIF に応じて低減し、複合材料の剛性もそれに応じて低減します。

エネルギー ベースの劣化

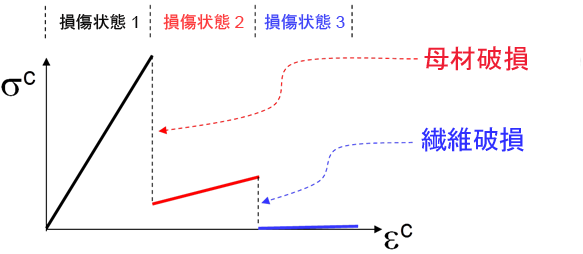
エネルギー ベースの劣化機能は、複合材料の積層内に含まれる複合材料の破損した単層の残留荷重を保持できる能力を考慮します。エネルギー ベースの劣化機能をアクティブにした場合、Helius PFA では、破損基準の始動後、複合材料の剛性を瞬間的にではなく、段階的に低減します。この場合、破損基準は単に破損の開始を特定します。破損基準の始動後、複合材料の構成剛性は、一連の個別の低減によって段階的に低減します。これらの低減は、ひずみ状態が破損開始時のレベルを超えて増加し続けると適用されます。この機能を使用する場合は、PFA 損傷状態変数を使用して、ひずみの増加に伴う複合材料の損傷の進展を特定することができます。エネルギー ベースの非線形機能の詳細な説明については、「理論マニュアル」を参照してください。どのような剛性低減が発生するかは、複合材料の破損状態によって完全に決定されます。

母材破損:

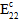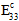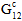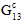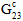母材破損の場合、複合材料 、、、、および は、次の関係を使用して線形に劣化します。

ここで、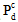 は劣化した複合材料特性、 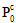はバージン複合材料特性です。また、dm は母材破損による劣化定数で次の方程式で示されます。

上記の方程式において、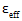 は、複合材料の有効なひずみ測定値で、次の方程式で示されます。

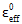は母材破損時の複合材料の有効なひずみ値です。また、 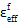は有効な最終ひずみ値で、次の方程式で示されます。

ここで、Gm は、母材破損前後に、複合材料で散逸されるエネルギーの合計です(MDE)。 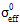は、方程式 A7.1 と同じ方法で計算された母材破損時の複合材料の有効な応力値です。Le は、Autodesk Inventor Nastran で定義された代表的な要素の長さです。

方程式 A5.4 で求めた有効な最終ひずみ値の定義では、A7.4 では、次に示すように、複合材料の有効な応力と有効なひずみの関係の線形劣化を仮定しています。

MCT 分解を変更せずに維持して、母材破損後の構成の応力を正確に取得するにはは、微視的から巨視的なスケールまで一貫した関係を保持するために、母材構成の特性も劣化されます。

繊維破損:

次のように有効なひずみ値を定義した母材破損による複合材料特性の劣化と同様の方法で、繊維破壊イベントの結果として複合材料の線形劣化 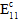、、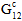 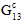が発生します。

有効な応力値も同様な方法で定義されます。ただし、縦方向せん断の低減は次の方程式で求めます。

これは、せん断剛性を有効なひずみの厳密な低減関数とします。

母材破損と繊維破損の主な違いは、構成情報を必要とするかどうかです。繊維が破損すると、母材も破損するものとみなされ、その後の破損計算には構成情報は必要ありません。このため、繊維破損後は構成の特性は更新されません。

したがって、母材破損イベントと繊維破損イベントの散逸エネルギーを入力することで、エネルギー ベースの劣化スキームが、破損イベント後の増加する複合材料のひずみ関数として、劣化した複合材料と構成の特性を計算できるようになります。エネルギー ベースの劣化は、一部のメッシュの最終解への依存を緩和し、堅牢な進行性破損解析を実現できます。

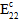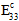注: 繊維破損前に母材構成が破損した場合、、、および 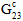は母材劣化エネルギーに応じて劣化します。それ以外の場合、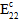、、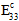および 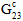は、繊維劣化エネルギーに応じて劣化します。

個別の間隔分割に関する注意:

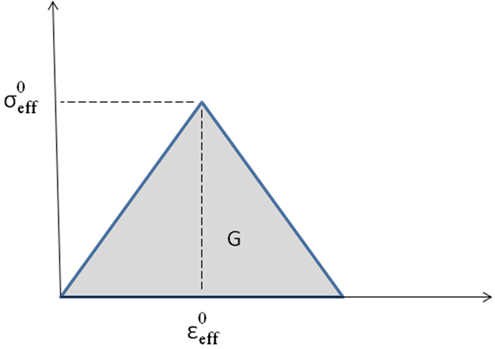
Helius PFA のエネルギー ベースの損傷機能は、下図に示すように、複合材料の線形劣化で複数の個別の間隔を使用します。各間隔は、特定の間隔での複合材料の応答を定義するセカント係数を使用します。エネルギーの合計が二等辺三角形に似た形を表す問題については、複合材料の応答が間隔内に正確にキャプチャされます。

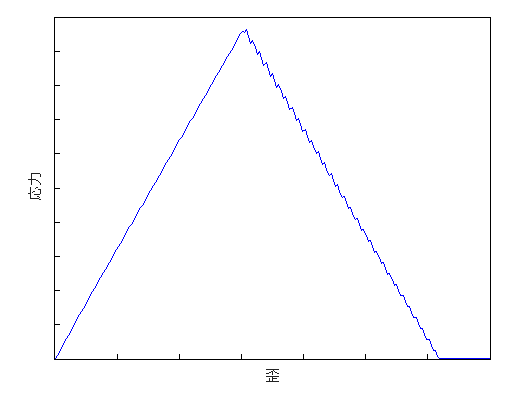
下図のように合計エネルギーが大きく歪んだ三角形を示す解析では、間隔分割は初期ひずみレベルの複合材料の線形軟化を正確に捉えることができません。これは、問題の最も迅速で堅牢な収束を達成するために使用する間隔数のみが原因で発生します。具体的には、破損間近のひずみレベルの応力のセカント間隔は高い剛性を保持し、複合材料の応力状態を間違って表示する原因となります。有効な最終ひずみ値が有効な初期ひずみ値の 100 倍を超える線形劣化曲線を定義する必要がある解析がある場合は、オートデスク サポートに連絡してください。