電磁場のモデリング
電磁誘導加熱現象は、マクスウェル方程式によって数学的に説明されています。
マクスウェル方程式は、微分形式で次のように記述することができます。
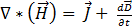 (アンペアの法則より) [1]
(アンペアの法則より) [1]
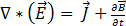 (ファラデーの法則より) [2]
(ファラデーの法則より) [2]
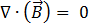 (ガウスの法則より) [3]
(ガウスの法則より) [3]
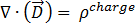 (ガウスの法則より) [4]
(ガウスの法則より) [4]
ここで、
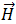 は磁場強度、
は磁場強度、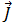 は伝導電流密度、
は伝導電流密度、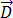 は電束密度、
は電束密度、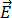 は電界、
は電界、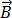 は磁束密度、
は磁束密度、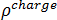 は電荷密度、
は電荷密度、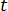 は時間です。
は時間です。
次の方程式に従って、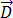 と
と 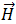 は誘電率の強磁性体特性の
は誘電率の強磁性体特性の  、および透磁率の
、および透磁率の 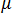 を介して
を介して 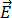 と
と 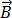 に関連付けることができます。
に関連付けることができます。
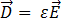 [5]
[5]
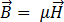 [6]
[6]
マクスウェル方程式は、オームの法則を使用してさらに次のように導くことができます。
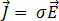 [7]
[7]
方程式 [5] と [7] を方程式 [1] に代入し、電流の周波数が 10 mHz 未満で、誘導電流 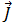 が、変位された電流密度
が、変位された電流密度 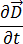 より大きいことを踏まえると、この項は無視することができるので、方程式 [1] は次のように記述できます。
より大きいことを踏まえると、この項は無視することができるので、方程式 [1] は次のように記述できます。
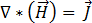 [8]
[8]
磁束密度 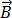 は、方程式 [3] の発散ゼロを満たすので、磁気ベクトル ポテンシャル
は、方程式 [3] の発散ゼロを満たすので、磁気ベクトル ポテンシャル 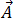 として次のように表すことができます。
として次のように表すことができます。
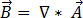 [9]
[9]
方程式 [9] を方程式 [2] に代入すると、次のようになります。
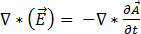 [10]
[10]
したがって次のようになります。
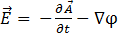 [11]
[11]
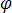 は、電気スカラ ポテンシャルです。方程式 [7] は次のようになります。
は、電気スカラ ポテンシャルです。方程式 [7] は次のようになります。
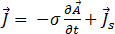 [12]
[12]
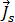 は、コイルのソース電流密度の振幅で、以下から導出されます。
は、コイルのソース電流密度の振幅で、以下から導出されます。
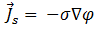 [13]
[13]
方程式 [6]、[9]、および [12] を方程式 [8] に代入すると、次のようになります。
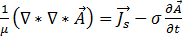 [14]
[14]
次に、ベクトル三重積方程式 [15] を、
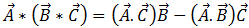 [15]
[15]
方程式 [14] に使用すると、次のようになります。
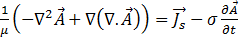 [16]
[16]
1 つの構成要素のベクトル ポテンシャル場は次のようになります。
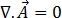 [17]
[17]
方程式 [16] は次のようになります。
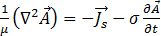 [18]
[18]
角振動数 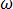 = 2
= 2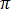 f、単位(rad/s)の正弦定常状態の場合、方程式 [18] は次のようになります。
f、単位(rad/s)の正弦定常状態の場合、方程式 [18] は次のようになります。
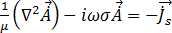 [19]
[19]
調和磁気ベクトル ポテンシャル 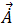 を解くと、磁場束密度は方程式 [9] で出すことができます。導体の調和誘導渦電流
を解くと、磁場束密度は方程式 [9] で出すことができます。導体の調和誘導渦電流 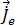 は、方程式 [20] によって導出されます。
は、方程式 [20] によって導出されます。
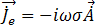 [20]
[20]
導体のジュール熱 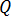 から、以下が判明します。
から、以下が判明します。
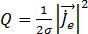 [21]
[21]
ジュール熱は、単位が (W/m3)の体積熱源で、導体の渦電流によって導出されます。
誘導加熱で発生する伝熱現象は、導体内の熱伝導であり、すべてのシミュレーションで使用される過渡熱伝導の方程式によって記述されます。
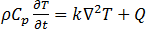 [22]
[22]
ここで、
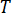 は温度
は温度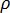 は密度です。
は密度です。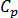 は比熱容量、
は比熱容量、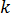 は材料の熱伝導率、
は材料の熱伝導率、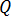 は方程式 [21] で出したジュール熱です。
は方程式 [21] で出したジュール熱です。