大きな圧力降下は、通常、フィードシステムのスプルー、ランナー、ゲートの間や金型入口などの縮流部を樹脂が通過するときに発生します。一般的に、圧力損失の 85% はダイの入口で、15% はダイの出口で発生します。

せん断粘度、流体慣性、および伸張粘度もジャンクチャー ロスの要因となります。ジャンクチャー ロス モデルは、圧力降下を特徴付ける流動実験から計算します。ジャンクチャー ロス モデルを使用することで、フィード システム内の圧力および流動バランスの予測を改善できます。

ジャンクチャー ロス モデルは、縮流部における、入口部の圧力降下(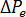)と壁面せん断応力(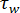)を関連付けます。

全体の(測定)圧力降下は、次のように定義されます。

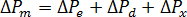
ここで、

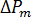• は測定圧力損失、
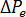• は入口ジャンクションでの圧力損失、
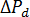• はダイ通過時の圧力損失、
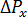• は出口ジャンクションでの圧力損失。

追加の圧力損失は、壁面せん断応力と圧力降下の関係で表します。

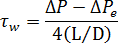
ここで、

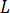• は長さ、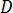
• は入口ジャンクションの直径。

これを次のように書き直すことができます。

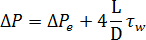
キャピラリー 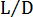VS 測定圧力降下のプロットでは、 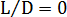における交点が追加の圧力損失となり、傾きは 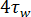に相当します。

実験では、追加の圧力損失 VS 壁面せん断応力のプロットで、さまざまな温度とせん断速度における追加の圧力損失結果は (特定の樹脂一般グレードに対して)、単一のマスター曲線に統合されることが確認されています。

Munstedt により開発された次の相関式は、キャピラリー データ解析で追加の圧力損失と壁面せん断応力の関係を示すために使用されます。[1]

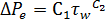
ジャンクチャー ロス係数とも呼ばれる(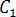 および 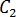)、材料の Bagley 補正定数は、さまざまなダイの長さを使用した一連のキャピラリー粘度実験から計算されます。異なるキャピラリー ダイ サイズを使用した測定を行い、ジャンクチャー ロスの補正をします。各実験の全体的な圧力降下は、有限差分法を使用してシミュレーションし、最適化手法を使用して、すべての WLF モデル定数、および 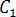と 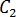定数における繰り返し計算を、予測圧力降下と測定圧力降下間の RMS 偏差が最小化するまで行います。

ここで、係数の範囲と標準値に注目します。

係数間には反比例関係があり、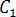 が増加すると、 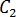は低減します。

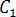= 1e-5～10 (標準値 0.0001)

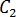= 2.5～1 (標準値 2)

選択した材料にジャンクチャー ロス データがない場合は、ジャンクチャー ロスが成形品において重大であるかを確認するには、充填解析(ジャンクチャー ロス係数の有無にかかわらず)を実行して確認できます。この目的のため、ジャンクチャー ロス係数に標準値を使用して、材料データにこの値を入力します。係数間には反比例関係があるため、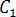 が増加すると、 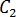は減少します。 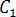値の範囲は 0.00001 から 10 (通常は 0.0001)で、 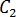値の範囲は 2.5 から 1 (通常は 2)です。ジャンクチャー ロスが成形品において重要であるとわかった場合は、ジャンクチャー ロス係数を取得するため、Autodesk Moldflow Plastics Labs による材料の測定を強く推奨します。

[1] Münstedt, H.1978.Viskositätsdaten von Kunststoffschmelzen, Kunststoffe 68: 92-98