The design flexural strength of a fully composite section is determined per ANSI/AISC 360-10 I3.2. During the design it is assumed that the nominal moment strength of the section can be calculated based on the plastic stress distribution on the composite section for the limit state of yielding (that is, the plastic moment). This assumption is valid for all standard W shapes in the AISC manual with F y <50 ksi.
The plastic stress distribution assumes that the steel is fully yielded (in compression or tension) and that the concrete stresses can be represented by an equivalent uniform stress block of intensity 0.85f c
There are generally two categories of solutions: the first in which the Plastic Neutral Axis (P.N.A.) falls within the concrete slab and the second in which the P.N.A. is in the steel section.
Plastic Neutral Axis in Concrete
The location of the P.N.A. is determined by first assuming that it falls in the concrete slab and then trying to calculate the depth of the equivalent concrete compressive stress block. If the P.N.A. falls within the slab, all of the steel section must have yielded first, and so the compressive force in the concrete stress block can be equated to the total tension in the steel:

where b e is the effective width of the concrete flange, A s is the cross-sectional area of the steel section, and a is the depth of the compressive stress block. By solving for a, the location of the P.N.A. (if a £ t s ) can be found, or the P.N.A. can be determined to be in the steel section (if a > ts ); an invalid condition because it would require more concrete than is available to balance the full tension in the steel).
If the location of the P.N.A. is confirmed to be within the concrete slab, then the nominal moment capacity of the composite section can be found by adding the moment contributions from the concrete compressive stress block and the steel area under tension. Thus:
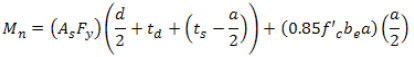
which can be simplified to:
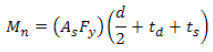
Plastic neutral axis in steel
If the depth of the compressive stress block a required to balance out the full tension of the steel exceeds the thickness of the slab ts , then there is not enough concrete to develop the full tensile strength of the steel, and the P.N.A. will fall within the steel.
Since all of the concrete will be in compression at the point of failure, the location of the P.N.A.
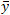 (measured as a distance from the bottom of the steel section) can be found by balancing the total compressive and tensile stresses:
(measured as a distance from the bottom of the steel section) can be found by balancing the total compressive and tensile stresses:
C c + C s = T s
The geometry of the compressive and tensile stress areas in the steel varies depending on where in the section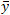 falls (the three possibilities are: in the top flange of the steel, in the fillet region between the top flange and the web, and in the web), but there is always a unique solution for
falls (the three possibilities are: in the top flange of the steel, in the fillet region between the top flange and the web, and in the web), but there is always a unique solution for
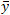 .
.
The P.N.A. can be tested for location within the top flange of the steel section by a method similar to the one used above for determining the location of the P.N.A. in the concrete slab - by defining a rectangular compressive stress block in the steel and equating the tensile and compressive stresses (for example, by assuming that the P.N.A. is located at the bottom of the top flange and checking equilibrium of tension and compression forces in the section, it can be determined if the P.N.A. lies within the top flange or below it). Determination of the P.N.A. in the web follows the same path.
In the case where the P.N.A. falls within the fillet region of the steel section, an approximation must be made on how to calculate the partial area of a fillet. The area of the fillets can be found exactly by subtracting the area of the two flanges and the web from the total steel cross-section, and the geometry of the fillet can be approximated by a triangle. Once a simplified geometry of the fillet is determined, calculation of the P.N.A. within the fillet is possible by calculating the partial area of a fillet.
The triangular approximation is made such that the area of a fillet (which can be determined by tabulated section dimensions) and the depth of the fillet are unchanged from their specified values. The width of the fillet k w for a triangular shape can be determined from those two constants.
If
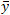 falls within the fillet (that is, t
f <
falls within the fillet (that is, t
f <
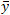 < k), the area of steel in compression can then be found by:
< k), the area of steel in compression can then be found by:
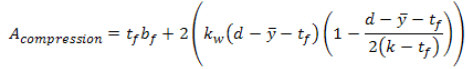
and therefore:
A tension = A s - A compression.
Rearranging and substituting allows for a unique solution for
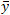 .
.
After the total area and stress distributions are known, the moment capacity can be determined by summing the product of each stress block and its lever arm. However, determining the centroid of the stress blocks in the steel section is greatly simplified if the entire beam is assumed to be in pure tension or pure non-composite bending, and then by adding tension or compression blocks to cancel out the difference.