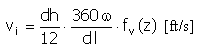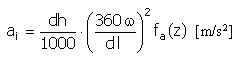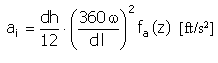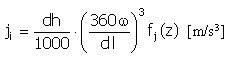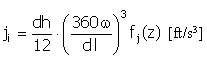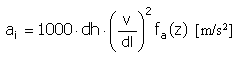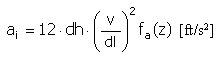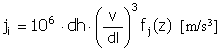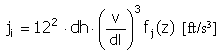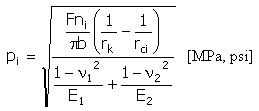캠 계산 공식

입력 데이터:

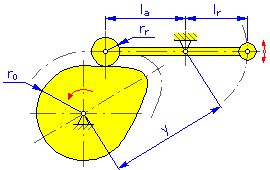
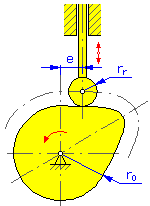
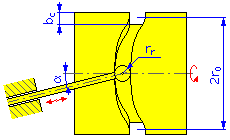
• 기본 반지름 r ₀ (디스크 및 원통형 캠)
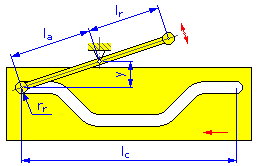
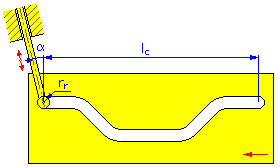
• 동작 길이 l _c (선형 캠)
• 캠 폭 b _c
• 롤러 반지름 r _r
• 롤러 폭 b _r (종동륜 쉐이프 원통의 경우)
• 편심률 e(종동륜 변환용 디스크 캠)
• 편심 각도 α(종동륜 변환용 선형 및 원통형 캠)
• 피벗 거리 y(스윙 암용 디스크 및 선형 캠)
• 암 길이 l _a (스윙 암용 디스크 및 선형 캠)
• 반작용 암 l _r (스윙 암용 디스크 및 선형 캠)
• 속도 ω(디스크 및 원통형 캠)
• 속도 v(선형 캠)
• 롤러에 작용하는 힘 F
• 가속된 무게 m
• 스프링 정격 c
• 허용 압력 p _A1
• 캠 재질의 탄성 계수 E ₁
• 캠 재질의 프와송의 비 μ ₁
• 허용 압력 p _A2
• 종동륜 재질의 탄성 계수 E ₂
• 종동륜 재질의 프와송의 비 μ ₂

디스크 캠
선형 캠
원통형 캠
외부 지름 = 2r 0 + b c
내부 지름 = 2r 0 - b c

캠 세그먼트

• 동작 함수 f _y (z) [ul]
• 반전 비율 k _r (선형 부품이 있는 포물선형 및 동작 포물선형만 해당)
• 선형 부품 k _l (선형 부품이 있는 동작 포물선형만 해당)
• 동작 시작 위치 l ₀ [°; mm, in]
• 동작 끝 위치 l [°; mm, in]
• 세그먼트 동작 길이 dl = l - l ₀ [°; mm, in]
• 시작에서 리프트 h ₀ [mm, in]
• 끝에서 리프트 h _max [mm, in]
• 세그먼트 리프트 d _h = h _max - h ₀ [mm, in]

리프트 종속성

디스크 및 원통형 캠

캠 회전 각도 ϕ _i [도]

세그먼트의 실제 상대적 위치: z _i = (ϕ _i - l ₀ ) / dl (범위 0 - 1)

리프트	y i = dh f y (z) [mm, in]
속도
가속도
펄스

선형 캠

캠 동작 위치 l _i [mm, in]

세그먼트의 실제 상대적 위치: z _i = (l _i - l ₀ ) / dl (범위 0 - 1)

리프트	y i = dh f y (z) [mm, in]
속도
가속도
펄스

동작 함수

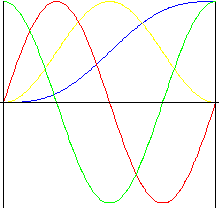
원형(확장 sinusoidal)

이 동작에는 뛰어난 가속도 특성이 있습니다. 소음, 진동 및 마모 수준이 낮기 때문에 주로 고속 캠에 사용됩니다.

	리프트
	속도
	가속도
	펄스

리프트	f y (z) = z - 0.5/π sin(2πz)
속도	f v (z) = 1 - cos (2πz)
가속도	f a (z) = 2π sin(2πz)
펄스	f j (z) = 4π 2 cos(2πz)

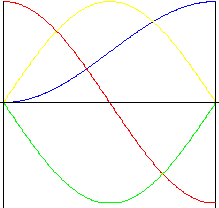
파형(sinusoidal)

이 곡선 고유의 장점은 스트로크 중 속도 및 가속도에서 부드럽게 나타나는 것입니다. 그러나 동작 시작 및 종료 시 가속도의 순간적인 변화로 인해 소음, 진동 및 마모가 생길 수 있습니다.

	리프트
	속도
	가속도
	펄스

리프트	f y (z) = 0.5 (1 - cos πz))
속도	f v (z) = 0.5 π sin (πz)
가속도	f a (z) = 0.5 π 2 cos(πz)
펄스	f j (z) = -0.5π 3 sin(πz)

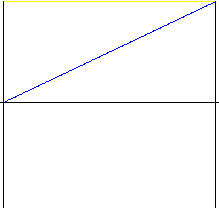
단위

동작 시작 및 종료 시 충격이 큰 간단한 동작입니다. 극히 단순한 장치를 제외하고 거의 사용되지 않습니다. 동작 시작 및 종료가 수정된, 즉 선형 부품이 있는 포물선형 동작을 사용하는 것이 좋습니다.

	리프트
	속도

리프트	f y (z) = z
속도	f v (z) = 1
가속도	f a (z) = 0
	주: z = 0 및 z = 1인 경우 적절한 값은 무한 값이어야 하지만 계산에서는 무한 값을 사용할 수 없으므로 영(0)을 사용합니다.
펄스	f j (z) = 0
	주: z = 0 및 z = 1인 경우 적절한 값은 무한 값이어야 하지만 계산에서는 무한 값을 사용할 수 없으므로 영(0)을 사용합니다.

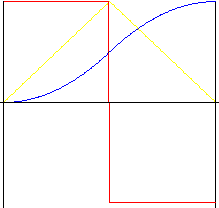
포물선형(2차 다항식)

가능한 한 가장 작은 가속도가 있는 동작입니다. 그러나 동작 시작, 중간 및 종료 시 갑작스러운 가속도의 변화로 인해 충격이 생길 수 있습니다. 반전비는 가속도 및 감속도 비율을 변경할 수 있도록 동작 중간에 "늘이기"를 허용합니다.

대칭형(반전비 k _r = 0.5)

	리프트
	속도
	가속도

	z = 0~0.5인 경우:
		리프트	fy(z) = 2z 2
		속도	fv(z) = 4z
		가속도	fa (z) = 4
		펄스	fa(z) = 0
	z = 0.5~1인 경우:
		리프트	fy(z) = 1 - 2(1 - z) 2
		속도	fv(z) = 4 (1 - z)
		가속도	fa (z) = -4
		펄스	fj(z) = 0
			주: z = 0 및 z = 1인 경우 적절한 값은 무한 값이어야 하지만 계산에서는 무한 값을 사용할 수 없으므로 영(0)을 사용합니다.

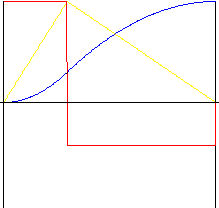
비대칭형

k _r - 반전비(범위 0.01~0.99)

	리프트
	속도
	가속도

	z = 0 to k r 인 경우:
		리프트	f y (z) = z 2 / k r
		속도	f v (z) = 2z / k r
		가속도	f a (z) = 2 / k r
		펄스	f j (z) = 0
	z = k r to 1의 경우:
		리프트	f y (z) = 1 – (1 – z) 2 / (1 – k r )
		속도	f v (z) = 2 (1 – z) / (1 – k r )
		가속도	f a (z) = -2 / (1 - k r )
		펄스	f j (z) = 0
			주: z = 0 및 z = 1인 경우 적절한 값은 무한 값이어야 하지만 계산에서는 무한 값을 사용할 수 없으므로 영(0)을 사용합니다.

선형 부품이 있는 포물선형

선형 동작보다 적합한 가속도 및 감속도를 제공합니다. 반전비는 가속도 및 감속도 비율을 변경할 수 있도록 동작 중간에 "늘이기"를 허용합니다. 선형 부품 비율을 사용하여 선형 동작 부품의 상대적 크기를 설정할 수 있습니다.

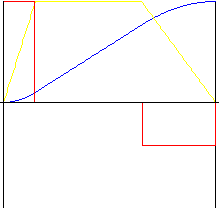
	속도
	가속도
	펄스

k _r - 반전비(범위 0.01~0.99)

k _l - 선형 부품 비율(범위 0~0.99)

k _z = 1 + k _l / (1 - k _l )

k _h = (1 - k _l ) / (1 + k _l )

	z = 0 to k r / k z 의 경우:
		리프트	f y (z) = k h z 2 k z 2 / k r
		속도	f v (z) = 2 k h z k z 2 / k r
		가속도	f a (z) = 2 k h k z 2 / k r
		펄스	f j (z) = 0
	z = k r / k z to r / k z + k l 의 경우:
		리프트	f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l )
		속도	f v (z) = 2 / (1 + k l )
		가속도	f a (z) = 0
		펄스	f j (z) = 0
	z = k r / k z + k l to 1의 경우:
		리프트	f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r )
		속도	f v (z) = 2 k h (1 - z) k z 2 / (1 - k r )
		가속도	f a (z) = -2 k h k z 2 / (1 - k r )
		펄스	f j (z) = 0

3차 다항식(3차 포물선)

포물선형 동작보다 충격이 작은 동작입니다.

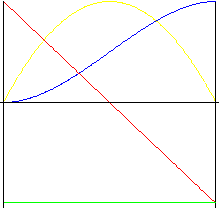
	리프트
	속도
	가속도
	펄스

리프트	f y (z) = (3 -2z) z 2
속도	f v (z) = (6 - 6z) z
가속도	f a (z) = 6 - 12z
펄스	f j (z) = -12

4차 다항식

3차 다항식 동작보다 충격이 작은 동작입니다.

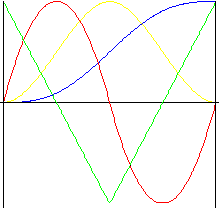
	리프트
	속도
	가속도
	펄스

z = 0 - 0.5인 경우
	리프트	f y (z) = (1 - z) 8z 3
	속도	f v (z) = (24 - 32z) z 2
	가속도	f a (z) = (48 - 96z) z
	펄스	f j (z) = 48 - 192z
z = 0.5~1인 경우:
	리프트	f y (z) = 1 - 8z (1 - z) 3
	속도	f v (z) = (32z - 8) (1 - z) 2
	가속도	f a (z) = (48 - 96z) (1 - z)
	펄스	f j (z) = 194z - 144

5차 다항식

3차 다항식 동작보다 충격이 작은 동작입니다.

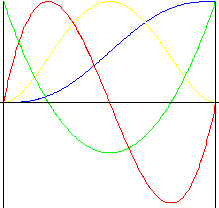
	리프트
	속도
	가속도
	펄스

리프트	f y (z) = (6z 2 - 15z + 10) z 3
속도	f v (z) = (z 2 - 2z + 1) 30z 2
가속도	f a (z) = (2z 2 - 3z + 1) 60z
펄스	f j (z) = (6z 2 - 6z + 1) 60

7차 다항식

펄스를 포함하여 모든 공식에서 부드럽게 나타납니다.

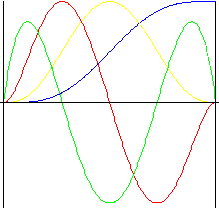
	리프트
	속도
	가속도
	펄스

리프트	f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4
속도	f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3
가속도	f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2
펄스	f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z

5차 비대칭 다항식

5차 다항식과 비슷하지만 강제 리프트 반전이 있습니다.

주: 부품 1과 부품 2를 조합해야 합니다.

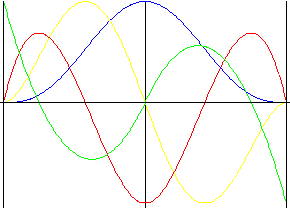
	리프트
	속도
	가속도
	펄스

부품 1
	리프트	f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3
	속도	f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3
	가속도	f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3
	펄스	f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40

부품 2
	리프트	f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3
	속도	f v (z) = (2z 3 - 3z 2 + 1) z 20/3
	가속도	f a (z) = (8z 3 - 9z 2 + 1) 20/3
	펄스	f j (z) = (4z 2 - 3z) 40

이중 파형

강제 리프트 반전이 있는 펄스를 포함하여 모든 공식에서 부드럽게 나타납니다.

주: 부품 1과 부품 2를 조합해야 합니다.

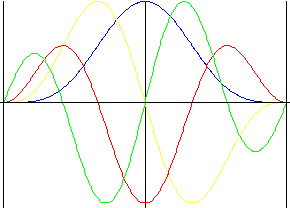
부품 1
	리프트	f y (z) = cos(0.5π (1 - z)) 4
	속도	f v (z) = π (0.5 sin(πz) - 0.25 sin(2πz))
	가속도	f a (z) = 0.5 π 2 (cos(πz) - cos(2πz))
	펄스	f j (z) = π 3 (-0.5 sin(πz) + sin(2πz))

부품 2
	리프트	f y (z) = 1 - cos(0.5π z) 4
	속도	f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz))
	가속도	f a (z) = 0.5 π 2 (cos(πz) + cos(2πz))
	펄스	f j (z) = -π 3 (0.5 sin(πz) + sin(2πz))

최대 상대 값 비교

동작	속도	가속도	펄스
원형(확장 sinusoidal)	2	6.28	39.5
파형(sinusoidal)	1.57	4.93	15.5
단위	1	∞	∞
포물선형(2차 다항식)	2	4	∞
3차 다항식	1.5	6	12
4차 다항식	2	6	48
5차 다항식	1.88	5.77	60
7차 다항식	2.19	7.51	52.5
비대칭 5차 다항식	1.73	6.67	40
이중 파형	2.04	9.87	42.4

기타 종속성

롤러 힘

F i = F + m a i + c y i [N, lb]

법선력

Fn i = F i / cos(γ i ) [N, lb]

모멘트

T i = F i r i tan (γ i ) [Nmm, lb in]

고유(헤르츠) 압력

	b = min (b v, b k )