Diversas curvas de transição são usadas na engenharia civil para gradualmente introduzir curvatura e superelevação entre as tangentes de curvas circulares, assim como entre duas curvas circulares com diferentes curvaturas.
Em sua relação com outras tangentes e curvas, cada espiral é uma curva de entrada ou uma curva de saída.
Os dois parâmetros mais comumente usados por engenheiros no projeto e definição de uma espiral são L (comprimento da espiral) e R. O parâmetro R refere-se ao raio de curvatura em uma extremidade da espiral. R1 e R2 podem ser usados para diferenciar entre o raio no início e no fim da espiral.
As ilustrações a seguir mostram os diversos parâmetros de uma espiral:
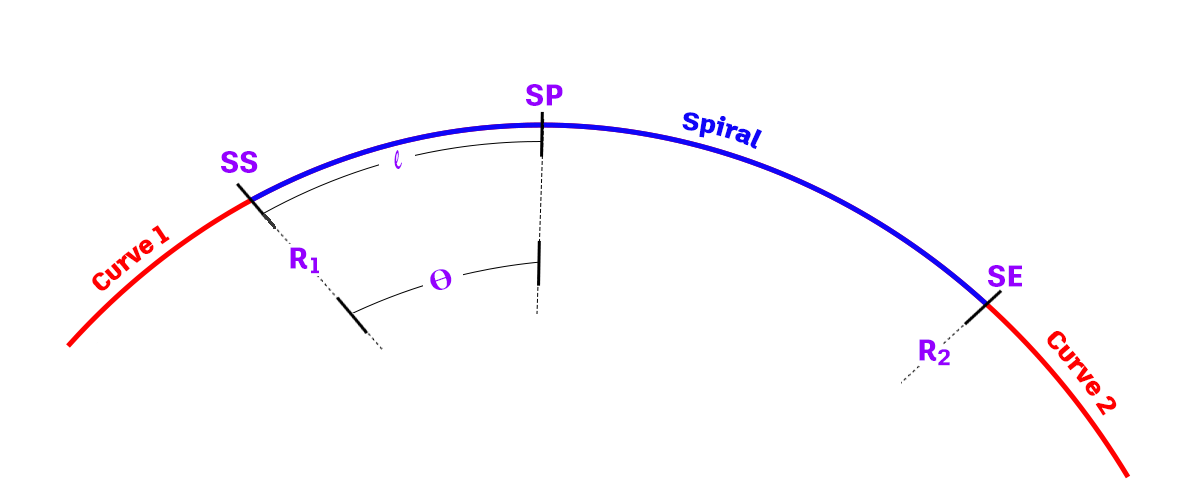
| Parâmetros de espiral | Descrição |
| R1 | O raio da curva 1. |
| R2 | O raio da curva 2. |
| SS | A posição inicial da espiral. |
| SE | A posição final da espiral. |
| SP | O ponto da espiral no comprimento do arco l. |
| Θ | O ângulo central no ponto da espiral no comprimento do arco l. |
| l | O comprimento do arco a partir da posição inicial da espiral ao longo da espiral. |
| L | Comprimento total do arco da espiral entre as posições inicial e final da espiral. |
Espiral composta
As espirais compostas fornecem uma transição entre duas curvas circulares com raios diferentes. Há dois tipos de espirais: simples e composta. Uma espiral composta consiste em uma curva formada por duas espirais simples. Ela contém dois segmentos, cada um dos quais é uma espiral simples, em uma união tangencial contínua com a espiral adjacente. Isso permite a continuidade da função da curvatura e oferece uma maneira de introduzir uma transição suave na superelevação.
Espiral Cornu
Embora o Autodesk Civil 3D seja compatível com diversos tipos de espiral, a espiral Cornu é o tipo de uso mais comum. A espiral Cornu é utilizada mundialmente em projetos de rodovias e ferrovias.
Primeiro investigada pelo matemático suíço, Leonard Euler, a função de curvatura Cornu é uma função linear escolhida para que a curvatura seja 0 (zero) como um função do comprimento onde a espiral encontra a tangente. A curvatura então aumenta linearmente até que seja igual a curva adjacente no ponto onde a espiral e curva se encontram.
Ao contrário da curva simples, ela também mantém a continuidade da curvatura local, o que é cada vez mais importante para veículos em velocidades mais altas.
Fórmula
As espirais de Cornu podem ser expressas nas seguintes fórmulas: 
- Θ= O ângulo central no ponto da espiral no comprimento do arco l.
- l = O comprimento do arco ao longo da curva.
Grau plano da espiral:
Ângulo total subentendido por espiral: 
A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:
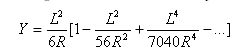
Espiral Bloss
Em vez de usar a Cornu, a espiral Bloss pode ser usada como transição. Esta espiral tem uma vantagem sobre a Cornu, no sentido que o P Invertido é menor e, portanto, há uma transição mais longa, como um extensão menor da espiral (K). Este fator é importante em projetos de ferrovia.
Fórmula
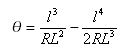
Outras expressões-chave:
A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:
Curvas senoidais
Estas curvas representam um curso consistente de uma curvatura e são aplicáveis à transição de 0 a 90 graus de deflexões de tangente. No entanto, as curvas senoidais não são utilizadas habitualmente porque são mais acentuadas que a de uma verdadeira espiral e, portanto, são difíceis de tabular e calcular.
Fórmula
- Θ= O ângulo central no ponto da espiral no comprimento do arco i.
- l = O comprimento do arco ao longo da curva.
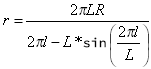
onde r é o raio da curvatura em qualquer ponto especificado.
Espiral senoidal de meio comprimento diminuindo na curva e tangente
Esta forma de equação é normalmente usada no Japão para projeto de ferrovia. Esta curva é útil em situações nas quais você precisa de uma transição eficiente na alteração da curvatura para baixos ângulos de deflexão (em relação à dinâmica do veículo).
Fórmula
Espiral senoidal de meio comprimento diminuindo na curva e tangente pode ser expressa como:
Onde 
e x é a distância do início até qualquer ponto na curva e é medida ao longo da tangente inicial (estendida); X é o total de X no final da curva de transição.
Outras expressões-chave:
A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:
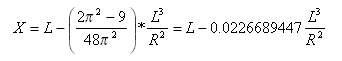
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:
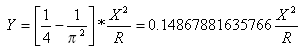
Parábolas cúbicas
As parábolas cúbicas convergem menos rapidamente do que espirais cúbicas, o que torna seu uso popular em projetos de ferrovias e rodovias.
Fórmula
Raio mínimo da parábola cúbica
Onde: Θ= O ângulo central no ponto da espiral no comprimento do arco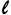 
.
Como referência, consulte o diagrama acima.
Uma parábola cúbica atinge o r mínimo em:
So 
O raio de uma parábola cúbica diminui de infinito para em 24 graus, 5 minutos e 41 segundos; daí em diante, começa a aumentar novamente. Isso torna as parábolas cúbica inúteis para deflexões maiores que 24 graus.
Cúbica (JP)
Essa transição foi desenvolvida para os requisitos no Japão. Algumas aproximações da Cornu foram desenvolvidas para usar em situações para acomodar um pequena ângulo de deflexão ou um raio grande. Uma desses aproximações, usada para projetos no Japão, é a Cúbica (JP).
Fórmula
A Cúbica (JP) pode ser expressa como:
Onde X = a distância tangencial no ponto de espiral-curva do ponto tangente-espiral.
Esta fórmula também pode ser expressa como:
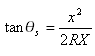
Onde 
é o ângulo central da espiral (mostrado como i1 e i2 na ilustração)
Outras expressões-chave:
A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:
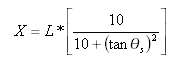
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:
Parábola cúbica NSW
Este é um tipo de parábola cúbica modificada para atender os requisitos das normas de New South Wales (Austrália).
Fórmula
A parábola cúbica NSW pode ser expressa como:
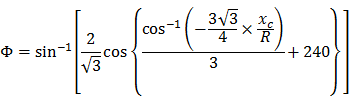
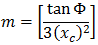
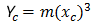
- Φ = ângulo entre a linha radial final em R e a linha perpendicular para a tangente inicial
- R = raio da curva
- Xc = total de X da espiral especificada
- Yc = total de Y da espiral especificada
Espirais bi-quadráticas (Schramm)
As espirais bi-quadráticas (Schramm) têm valores baixos de aceleração vertical. Elas contêm duas parábolas de segundo grau cujo raio varia como uma função do comprimento da curva (l).
Fórmula de curva simples
Curvatura da primeira parábola:
para 
Curvatura da segunda parábola:
para 
Esta curva é especificada pelo comprimento (L) definido pelo usuário da curva de transição.
Fórmula de curva composta
Curvatura da primeira parábola:
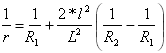para 
Curvatura da segunda parábola:
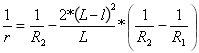para 