Para selecionar as configuração de simulação dinâmica

Uma vez que tenha definido estas opções, elas afetarão a simulação dinâmica até que sejam alteradas. Defina as opções imediatamente após abrir a simulação dinâmica.

1. Na faixa de opções, clique na guia Ambientes painel Iniciar Simulação dinâmica para exibir os painéis Simulação dinâmica.
2. Em seguida, clique na guia Simulação dinâmica painel Gerenciar Configurações de simulação .
3. Clique em Converter automaticamente restrições em juntas padrão para ativar o Conversor automático de simulação dinâmica (Motor de redução de restrições ou MRR).

   A opção padrão está ativada.

   Ao clicar em OK, o motor de redução de restrições converte automaticamente as restrições da montagem em juntas padrões e atualizará as juntas convertidas na próxima vez que for aberto o mecanismo.

4. Se desejar ser avisado quando um mecanismo estiver sobrerrestringido, clique em Avisar quando o mecanismo estiver sobrerestringido.

   Ainda que este ajuste seja o padrão para os mecanismos novos, não está ativado como padrão nos mecanismos criados antes da versão 2008. Ao ativar esta opção, se o mecanismo estiver sobrerrestringido, o software exibirá uma mensagem após se clicar em OK e antes de criar as juntas padrões automaticamente.

5. Se deseja obter uma indicação visual dos componentes incluídos nos diferentes grupos móveis, selecione a caixa de verificação Colorir grupos móveis. As anulações de cores pré-definidas são atribuídas aos componentes do mesmo grupo móvel. Esta opção ajuda a analisar as relações entre os componentes. Para voltar os componentes às suas cores atribuídas padrão, desative a caixa de verificação da caixa de diálogo de configurações ou clique com o botão direito no nó Grupos móveis e selecione Colorir grupos móveis
6. Clique em Todas as posições iniciais a 0,0 caso queira definir todas as posições iniciais do grau de liberdade em 0 sem alterar a posição atual do mecanismo.

   Isto é útil para visualizar as impressões variáveis que começam em 0 no gráfico de saída.

7. Clique em Restabelecer todos para restabelecer todos os sistemas de coordenadas às suas posições iniciais dadas durante a construção do sistema de coordenadas de junta .

   Este é o ajuste padrão.

8. Clique Análise de tensão AIP para preparar toda a informação FEA para análise pela Análise de tensão AIP.

   Esta função salva os dados relevantes para a FEA nos arquivos de peça das peças selecionadas.

9. Outra alternativa é clicar Simulação ANSYS para preparar um arquivo contendo toda a informação FEA para exportar à ANSYS.

   Esta função salva os dados relevantes para a FEA em um arquivo legível para ANSYS.

   • Na caixa de entrada de texto, insira o nome do arquivo que deseja arquivar as informações da FEA que serão exportadas à ANSYS.
   • Também é possível clicar em Salvar em, para especificar um arquivo existente ou criar um arquivo.

     Se seleciona um arquivo existente, o software anula todos os dados contidos no arquivo.

     Nota: Ao utilizar a versão 10 ou 11 do Ansys Workbench, deve-se fazer outra modificação no arquivo. Abra o arquivo de texto, localize a seção chamada “Estado inercial.” Nesta seção, há duas linhas que devem ser removidas. As linhas são “Fixadas” e o código associado, pode ser tanto “0” ou “1” na linha seguinte.
10. Clique em Mais para visualizar mais propriedades.
11. Para exibir a informação de direitos autorais nos arquivos AVI, clique em Exibir direitos autorais em AVIs e insira a sua informação na caixa de entrada de texto.
12. Clique em Velocidade angular de entrada em revoluções por minuto (rpm) para inserir as velocidades angulares em rpm.

    No entanto, o resultado fica localizado nas unidades definidas quando se seleciona o arquivo de montagem vazio.

13. Para definir o comprimento do eixo Z do sistema de coordenadas de montagem para estruturas 3D na janela de desenho, insira o valor da percentagem na caixa de edição de tamanho do eixo Z.

    Por padrão, o tamanho do eixo Z é igual a 20% da diagonal da caixa delimitadora.

14. Clique em OK ou em Aplicar.

    Ambos salvam as configurações, mas OK também fecha esta caixa de diálogo.

Modelo de micromecanismo

Esta opção foi projetada para utilizar mecanismos com propriedades de massa pequenas.

No modo padrão, o cálculo falha se a massa ou a inércia forem inferiores a 1e-10 kg ou 1e-16 kg.m2. As equações dinâmicas são então resolvidas com um procedimento gaussiano e com a precisão estabelecida em 1e-10 (abaixo deste valor, o eixo é estabelecido em 0).

Se o Modo de micromecanismo estiver ativado, a massa ou a inércia devem ser superiores a 1e-20 kg e 1e-32 kg.m2. A precisão gaussiana é estabelecida em 1e-32.

Para saber quando ativar esta opção, verifique as propriedades de massa fornecidas pelo sistema de coordenadas de junta.

• Se existir um grau de liberdade de translação, devemos verificar a massa.
• Se existir um grau de liberdade de rotação no eixo X, devemos verificar a inércia principal Ixx no eixo X, não as inércias cruzadas Ixz e Ixy, já que estas não interessam neste momento.

Exemplo 1
Em um mecanismo onde a peça menor tem uma massa m = 6,5e-9 kg e inércias principais Ixx = 1e-20 kg/m2, Iyy = 1e-20 kg.m2, mesmo que o Izz > limite de inércia = 1e-10 kg.m2:
	Se esta peça só tem um grau de liberdade de rotação no eixo Z, o modo Micromecanismo não é necessário, já que Izz > limite de inércia = 1,0e-10 kg.m2 Se esta peça só tem grau de liberdade de translação

Atenção: O Modelo de micromecanismo só é ativado quando são simulados mecanismos pequenos. Ao mesmo tempo, deve-se alterar a opção Precisão de montagem a fim de otimizá-la para as peças pequenas. Consulte Precisão de montagem para obter mais informações.

Precisão de montagem

É aplicado unicamente a contornos fechados e juntas de contato 2D.

Contato 2D: define a distância máxima permitida entre pontos de contato. O valor padrão é 1e-6m = 1μm.

• Esta distância sempre é verificada ao final dos passos Runge-Kutta.
• Se a distância entre os pontos não ultrapassa a precisão da montagem, são aceitas as posições e as velocidades e o cálculo prossegue com a estimativa dos erros de integração.
• Se a distância ultrapassa a precisão da montagem, são corrigidas as posições até que a distância não exceda a precisão da montagem. A seguir, baseadas nas novas posições, são corrigidas as velocidades e o cálculo prossegue com a estimativa dos erros de integração.

Contorno fechado: igual ao Contato 2D, mas também pode ter restrições angulares (expressadas em radianos) baseadas no tipo de junta.

• A distância e as restrições angulares são verificadas ao final dos passos Runge-Kutta.
• Se as restrições de distância não ultrapassam a precisão da montagem e se as restrições angulares também não ultrapassam a precisão da montagem multiplicada por 1e 3 (com a precisão da montagem expressada em metros), são aceitas as posições e as velocidades, e o cálculo prossegue com a estimativa dos erros de integração.
• Caso contrário, são corrigidas as posições até que as restrições de distância não ultrapassem a precisão da montagem e as restrições angulares não ultrapassem a precisão da montagem multiplicada por 1e 3. A seguir são corrigidas as velocidades e o cálculo prossegue com a estimativa dos erros de integração.

Modificação da precisão da montagem

O parâmetro Precisão de montagem pode ser alterado nos seguintes casos:

• O mecanismo não pode ser montado no início ou durante a simulação. Em primeiro lugar, verifique a viabilidade do mecanismo (se a posição solicitada é real e pode ser executada pelo mecanismo. Verifique os movimentos impostos que possam levar à posições contraditórias). Se não for detectado nenhum problema e se a escala do mecanismo é grande (da ordem de 1 m), aumente então a precisão da montagem (1e-5m ou 1e-4m). Se a escala é pequena (menor que 10 mm), reduza então a precisão da montagem (1e-7m ou 1e-8m).
• Em casos onde o mecanismo seja inferior a 1 mm, reduza a precisão da montagem (na faixa 1e-8m/1e-10m) ou utilize o Modelo de micromecanismo.

Atenção: Não imponha nenhuma precisão de montagem inferior a 1e-12. Não adiciona nenhum valor e pode causar problemas na simulação.

Precisão do solucionador

As equações dinâmicas são integradas usando um esquema de integração de Runge-Kutta de quinta ordem. O erro e o intervalo de tempo da integração são gerenciados do modo seguinte para que possam garantir aceitação:

• No final de cada passo Runge-Kutta, é estimado o erro de integração, baseado nas velocidades e acelerações calculadas.
• Este erro de integração é comparado ao parâmetro “precisão do solucionador” definido pelo usuário.
• Se o erro de integração não ultrapassa a precisão do solucionador, o passo é aceito e a integração continua.
• Se o erro de integração ultrapassa a precisão do solucionador, o passo é recusado. Então é calculado um novo intervalo de tempo inferior ao passo real e é reiniciada a simulação desde o princípio do passo com o novo valor do intervalo de tempo.

O erro de integração é calculado utilizando determinadas propriedades das fórmulas de Runge-Kutta. Permite calcular facilmente as posições “p” e as velocidades “v” de quinta ordem (vetores com notação “p5” e “v5” respectivamente) e de quarta ordem (vetores com notação “p4” e “v4”). O erro de integração é então definido nas posições e velocidades seguintes:

Integ_erro_position = norm(p5 - p4) Integ_erro_velocity = norm(v5 - v4) Onde norm indica uma norma especial.

Quando um passo é aceito, são estabelecidas as seguintes relações (em unidades métricas):

Integ_erro_position = norm(p5 - p4) < Atol + | p5 | . Rtol Integ_erro_velocity = norm(v5 - v4) < Atol + | v5 | . Rtol

Com:

	Atol	Rtol
Grau de liberdade de translação	Precisão do solucionador Padrão = 1e-6 Sem valor máximo	Precisão do solucionador Padrão = 1e-6 Sem valor máximo
Grau de liberdade de rotação	Precisão do solucionador 1e 3 1e 3 Padrão = 1e-3 Valor máximo = 1e-2	Precisão do solucionador 1e 3 1e 3 Padrão = 1e-3 Valor máximo = 1e-2

Para ilustrar este processo, considere os seguintes exemplos:

Exemplo 1: Ilustra um erro relativo Rtol
Tipo de junta: junta deslizante 1 com posição e velocidade
	p[1] = 4529,289768 m v[1] = 18,45687455 m/s
Se a precisão do solucionador é estabelecida em 1e-6 (valor padrão), são garantidos resultados de seis dígitos:
	p[1] = 4529,28 m v[1] = 18,4568 m/s
Se a precisão do solucionador é estabelecida em 1e-8, são garantidos oito dígitos:
	p[1] = 4529,2897 m v[1] = 18,456874 m/s
Exemplo 2: Ilustra um erro relativo para Atol
Tipo de junta: junta deslizante 1 com posição e velocidade
	p[1] = 0,000024557 m v[1] = 0,005896476 m/s
Se a precisão do solucionador é estabelecida em 1e-6 (valor padrão), são garantidos resultados de seis casas decimais:
	p[1] = 0,000024 m v[1] = 0,005896 m/s
Se a precisão do solucionador é estabelecida em 1e-8 (valor padrão), são garantidos resultados de oito casas decimais:
	p[1] = 0,00002455 m v[1] = 0,00589647 m/s
O mesmo raciocínio é aplicado para as juntas de pino, mas Atol e Rtol têm uma precisão de solucionador multiplicada por 1e 3:
Exemplo 3: Ilustra um erro relativo para Rtol
Tipo de junta: junta de pino 2 com posição e velocidade
	p[2] = 12,53214221 rad v[2] = 21,36589547 rad/s
Se a precisão do solucionador é estabelecida em 1e-6 (valor padrão), são garantidos resultados de três dígitos:
	p[2] = 12,5 rad v[2] = 21,3 rad/s
Se a precisão do solucionador é estabelecida em 1e-8, são garantidos cinco dígitos:
	p[2] = 12,532 rad v[2] = 21,365 rad/s

O parâmetro Precisão do solucionador pode ser alterado nos seguintes casos:

• A simulação é interrompida com uma mensagem de erro e o intervalo de tempo é pequeno o suficiente para garantir resultados de qualidade. Se há pequenas deslocações, reduza a precisão do solucionador. Se há grandes deslocações, aumente a precisão do solucionador.
• Quando são ativados contatos 2D (estado = 1). Se há pequenas forças, reduza a precisão do solucionador. Se há forças grandes, aumente a precisão do solucionador. Não é válido para forças em momentos de impacto.
• Quando trabalhar com mecanismos pequenos (menores que 1 mm). Nestes casos, reduza a precisão do solucionador ou selecione a opção Modelo de micromecanismo.

Atenção: A precisão do solucionador está diretamente relacionada com o tamanho do intervalo de tempo. Não reduza muito a precisão do solucionador (por exemplo, abaixo de 1e-12). Ao fazê-lo, afetará consideravelmente o tempo de simulação.

Velocidade de captura

Este parâmetro é utilizado para simular impactos entre objetos. Ajuda o solucionador a limitar o número de rebotes pequenos antes dos resultados de contato constante. O modelo de impactos utiliza um coeficiente de restituição “e”. O valor é especificado pelo usuário e varia de 0 a 1. Nestas condições, os valores são tratados da seguinte forma:

• Quando e = 0, há uma dissipação máxima de energia. Por exemplo, tomemos o caso de uma bola normal que cai sobre um plano de uma altura inicial, sem velocidade inicial e sob o efeito da gravidade: não é observado nenhum rebote e o estado do contato é = 1.
• Quando e = 1, não há dissipação de energia. Usando o exemplo da bola, esta rebota até sua posição inicial e o estado do contato seja = 0,5. O movimento é periódico e prossegue infinitamente.
• Quando e>0 e e< 1, há dissipação de energia em cada impacto. Usando novamente o exemplo da bola, esta rebotará, mas a altura do rebote é reduzida depois do primeiro impacto até chegar ao limite. Para estas condições deve-se utilizar a velocidade de captura.

O parâmetro Velocidade de captura ajuda o solucionador a limitar o número de pequenos rebotes que ocorrem antes do contato ser considerado ativo ou constante. O processo de captura é produzido da seguinte maneira:

• É calculado o impacto com todos os coeficientes de restituição estabelecidos em seus valores iniciais.
• As velocidades relativas ao pós-impacto, que representam as velocidades de lançamento, são comparada com o parâmetro de velocidade de captura em todos os contatos.
• Se todas as velocidades relativas forem mairoes que a velocidade de captura ou nulas, o impacto é aceito e o solucionador avança no tempo usando as novas velocidades como parâmetros iniciais.
• Se a velocidade relativa é inferior à velocidade de captura e não é nula, e = 0 é imposto a esse contato para que possa maximizar a perda de energia e o impacto ser calculado novamente. Se for aceito o impacto, todos os coeficientes de restituição serão reajustados aos seus valores iniciais.

Atenção: O estado do contato (e = 1) nunca é imposto de forma programática. O solucionador administra o estado do contato de forma que todos os contatos ativos sejam coerentes. O solucionador executa o cálculo com uma equação quadrática não linear.

Quando pode ser alterado o parâmetro?

Este parâmetro pode ser alterado no seguinte caso:

• Quando existirem contatos 2D e a simulação estiver lenta. Pare a simulação e trace a velocidade de captura. Se o parâmetro variar em cada intervalo de tempo (entre 0 - 1 - 2) ou se for igual a 1, há um erro de captura. O solucionador tenta estabilizar o estado dos contatos, mas é um processo longo e complicado. Neste caso, aumente a velocidade de captura.
• Não há nenhum benefício em reduzir o valor do parâmetro.

Velocidade de regularização

Nos contatos 2D, é utilizada uma lei de atrito real não linear de Coulomb. Nas juntas e nos contatos 3D, para simplificar e para evitar estados hiperestáticos, é usada uma lei regularizada de Coulomb, que pode ser ilustrada do seguinte modo:

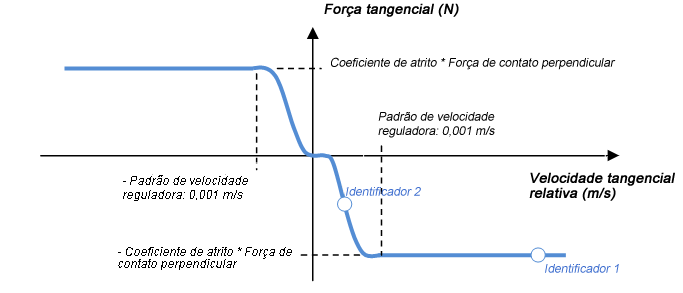
A regularização é definida pelo parâmetro de regularização de velocidade.

Com este modelo, em casos de contato de fixação (ou contato de giro), se a velocidade tangencial relativa é zero, a força tangencial é nula.

No caso da atrito de juntas em um grau de liberdade de giro, a força tangencial é substituída por um torque tangencial (unidade: Nm) e a velocidade relativa tangencial é uma velocidade de giro (unidade: rad/s). Ambas são calculadas multiplicando a força tangencial e dividindo a velocidade de translação pelo raio da junta.

Exemplo 1
Uma junta de pino com um raio de 10 mm é dirigida com uma velocidade constante “w” de 10 rad/s. Aplicamos uma força (Fn) de 20 N à junta, perpendicular a seu eixo de rotação e definimos um fator de atrito (mu) de 0,1. Neste caso, o par de atrito (Uf) da junta pode ser calculado do modo seguinte:
	? = r * w = 0,01 * 10 = 0,1 m/s ? > velocidade de regularização = 0,001 m/s => Uf = -mu * r * Fn = -0,1 * 0,01 * 20 = -0,02 Nm Consulte “identificador 1” no gráfico regularizado de Coulomb.
Exemplo 2
Usando o mesmo exemplo, mas com uma velocidade (w) de 0,05 rad/s, o torque de atrito (Uf) vem determinado por:
	? = r * w = 0,01 * 0,05 = 0,0005 m/sm ? > velocidade de regularização = 0,001 m/s => Uf ≈ -mu * r * Fn/2 = -0,1 * 0,01 * 20/2 = -0,01 Nm Consulte o “identificador 2” no gráfico regularizado de Coulomb.

O parâmetro Velocidade de regularização pode ser alterado nos seguintes casos:

• A simulação é lenta e são produzida pequenas oscilações em uma junta com atrito ou em uma Junta de contato 3D. A atrito da junta ou do contato 3D cria uma rigidez considerável no modelo, de maneira que o solucionador reduz o intervalo de tempo para assegurar uma precisão confiável. Deve reduzir a rigidez => aumentar o parâmetro velocidade de regularização em um fator de 5 (5e-3 m/s). Se o modelo ainda estiver lento, é possível aumentar mais o parâmetro usando valores relacionados com o seu modelo (inferiores, comparados às velocidades do seu modelo).
• Não aumente muito a velocidade de regularização; caso contrário, isto só funcionará entre estes valores. A força de atrito nunca atingirá seu valor máximo. Este resultado é um limite artificial no efeito da atrito.

Validação numérica

Antes de analisar os resultados da simulação, é importante verificar que a simulação é numericamente válida, isto é, não depende de parâmetros numéricos. Para executar o passo de validação numérica, faça o seguinte:

1. Execute uma simulação com um conjunto de parâmetros numéricos (precisão de solucionador e de montagem, velocidade de captura, velocidade de regularização e intervalo de tempo) e, a seguir, salve-a.
2. Divida o parâmetro por 10, para cada um deles, execute a simulação e salve-a.
3. Imprima todos os resultados no mesmo gráfico. Se os resultados são parecidos, a simulação não depende de parâmetros numéricos. Caso contrário, há uma questão de sensibilidade.
4. Se a simulação não depende de parâmetros numéricos, é possível analisar os resultados.
5. Se depende de parâmetros numéricos, utilize as curvas resultantes para determinar quais parâmetros numéricos provocam o problema. Divida este parâmetro por 10 e tome o valor resultante como valor nominal para o parâmetro numérico. Reinicie a validação desde o princípio. Para poupar tempo, é possível validar a não dependência para um único parâmetro.