Este programa gera um projeto preliminar para a folga diametral do diâmetro do pino de articulação do rolamento especificado e velocidade. O valor da folga diametral é determinado mediante uma folga diametral relativa, que é calculado de acordo com a fórmula empírica:
onde:
| Ψ |
folga diametral relativo [-] |
|
|
v H |
velocidade circunferencial do pino de articulação [m s -1 ] |
A folga diametral relativa é um parâmetro de projeto importante que afeta as propriedades do rolamento. Sua faixa é geralmente de 0,0005 até 0,004. Os valores baixos da folga diametral relativa são adequados para rolamentos que têm uma alta pressão específica e funcionam com velocidades de deslizamento baixas ou vice-versa.
Com um valor cada vez maior da folga diametral relativa, a capacidade de carga do rolamento cai e o risco de vibrações do pino de articulação e cavitações do revestimento do rolamento aumentam. A velocidade de deslizamento do pino de articulação tem um efeito muito significativo na seleção da folga diametral. A seleção deve ser feita de acordo com o material do revestimento e o uso:
|
Babbitt |
(0.5 ~ 1) .10 -3 |
|
Bronzes |
(0.8 ~ 2) .10 -3 |
|
Ligas de alumínio |
(1.2 ~ 2.5) .10 -3 |
|
Ferro fundido, grafite |
(2 ~ 3) .10 -3 |
|
Plásticos |
(1.5 ~ 10) .10 -3 |
Os valores mais baixos são selecionados para rolamentos estreitos e precisos, já que não há carga nas arestas.
Redução do diâmetro da bucha interna devido à pressão no alojamento do rolamento:
Ao pressionar uma bucha no alojamento do rolamento com interferência relativa:
aparece certa pressão de contato:
onde:
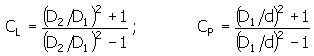 |
Tamanho recomendado da interferência relativa:
ϑ ≈ 1.3. 10 -3 : gabinete de rolamento de liga de alumínio;
ϑ ≈ 0.6. 10 -3 : gabinete de rolamento de ferro fundido ou aço.
A alteração da folga diametral devido à pressão da bucha é determinada pela seguinte equação:
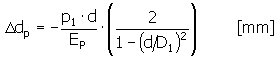
Alteração da folga diametral devido aos gradientes da temperatura radial:
As peças do rolamento se dilatam pelo aumento do calor durante o funcionamento. Sob à influência dos gradientes de temperatura radial, uma alteração no jogo diametral radial acontece e o seu valor é:
Δ φ T = (α L - α H ) (1 - B) (T V - T U ) - 0,6 (α L Δ T rL - 0,75 α H Δ T rH
onde:
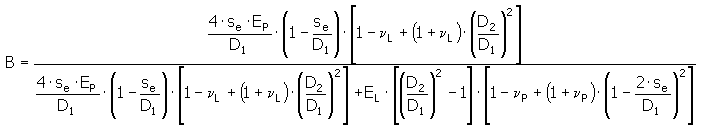 |
enquanto a espessura efetiva da bucha é: s e = (D1 - d s V ) / 2 [mm]
o gradiente de temperatura radial entre a superfície exterior do rolamento e a superfície de deslizamento é:
ΔT rL ≈ 5 ... 15 [°C]
o gradiente de temperatura radial entre a superfície de deslizamento e o centro do eixo é:
ΔT rH 11.0pt ≈ 2 ... 5 [°C]
A alteração da folga diametral devido aos gradientes de temperatura radial é determinada pela seguinte equação:
Δd T =Δφ T d [mm]
Significado das variáveis utilizadas:
|
d |
Diâmetro de pino de articulação [mm] |
|
D 1 |
Diâmetro interno do corpo do rolamento [mm] |
|
D 2 |
Diâmetro externo do corpo do rolamento [mm] |
|
Δd p |
Alteração da folga diametral por fixação da bucha devido à pressão [ mm] |
|
ΔdT |
Alteração da folga diametral devido aos gradientes de temperatura radial [mm] |
|
Δd 1 |
Valor médio de interferência da pressão da bucha para dentro do corpo do rolamento [μm]. |
|
E L |
Módulo de elasticidade do material do corpo do rolamento [MPa]. |
|
E p |
Módulo de elasticidade do material da bucha [MPa]. |
|
S e |
Espessura efetiva da bucha [mm] |
|
S v |
Espessura do revestimento da bucha [mm] |
|
T U |
Temperatura da área circundante mais próxima ao rolamento [°C]. |
|
T v |
Temperatura média do lubrificante na saída do rolamento [°C]. |
|
ΔT |
Queda da temperatura radial entre a superfície exterior do rolamento e a superfície de deslizamento [°C]. |
|
ΔT rH |
Queda da temperatura radial entre a superfície exterior do rolamento e a superfície de deslizamento [°C]. |
|
ΔT rL |
Queda da temperatura radial entre a superfície de deslizamento e o centro do eixo [°C]. |
|
α L |
Fator de dilatação térmica do corpo do rolamento [°C -1 ]. |
|
α H |
Fator de dilatação térmica do material do pino de articulação do rolamento [°C -1 ]. |
|
ν L |
Coeficiente de Poisson do material do corpo do rolamento [-] |
|
ν p |
Coeficiente de Poisson do material da bucha [-] |
| υ |
Interferência relativa [-] |