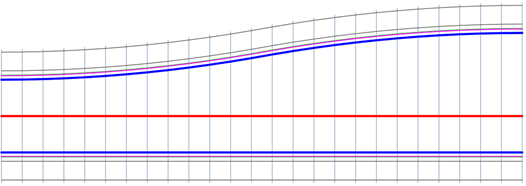
С помощью панорамного вида «Переход коридора» можно создавать и редактировать переходы коридора.
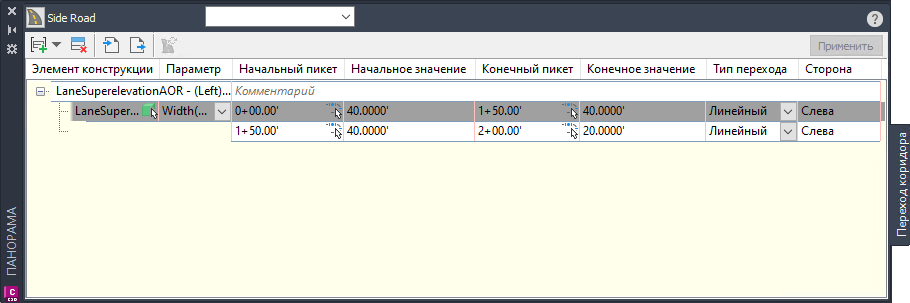
При выборе команды «Редактировать переход коридора» отображается панорамный вид «Переход коридора», а в командной строке появляется запрос на выбор элемента конструкции для перехода.
Используя запросы в командной строке, выберите элемент конструкции для перехода, параметр для перехода, а затем пикеты, значения и тип перехода.
Значения можно также задать в панорамном виде «Переход коридора».
При выборе строки в панорамном виде соответствующий переход выделяется на чертеже синими обозначениями.
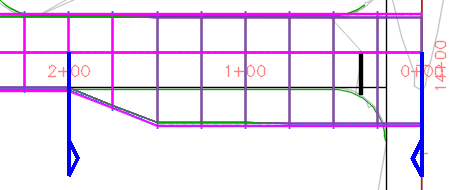
Типы переходов
Можно создать несколько разных типов переходов.
Линейный
Простой линейный переход, где каждый рассчитываемый пикет основан на следующей формуле:
начальное значение + ((расстояние от начального пикета / общее расстояние) * дельта)
где:
дельта = значение конечного перехода - значение начального перехода
дельта пикета = расстояние от начального пикета / общее расстояние перехода
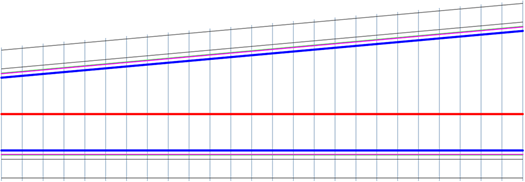
Сужение площадки
Переход по S-образной кривой, в котором используются следующие формулы.
Для первых 33,33 % расстояния перехода:
начальное значение + ((((дельта пикета * 3) ^ 2) * (дельта / 4))
С 33,33 % до 66,66 % расстояния перехода:
начальное значение + (дельта / 4) + (((дельта пикета * 3) -1) * (дельта / 2))
С 66,66 % до конца расстояния перехода:
конечное значение - ((((1 - дельта пикета) * 3) ^ 2) * (дельта / 4))
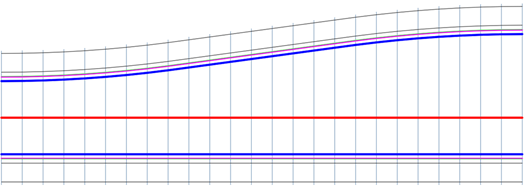
Кубический вход
Кубический переход с расширением, которое возникает в начале перехода и сжимается к его концу.
Для этого перехода используется следующая формула:
конечное значение - (((1 - дельта пикета) ^ 3) * дельта)
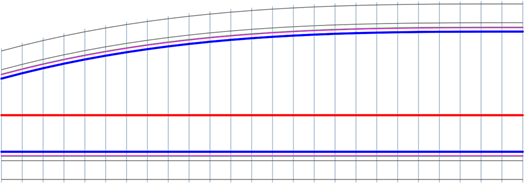
Кубический выход
Кубический переход с расширением, которое возникает в конце перехода и сжимается к его началу.
Для этого перехода используется следующая формула:
начальное значение + (дельта пикета ^ 3) * дельта
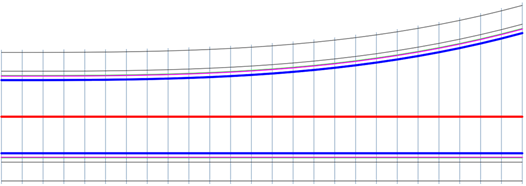
Параболический вход
Параболический переход с расширением, которое возникает в начале перехода и сжимается к его концу.
Для этого перехода используется следующая формула:
конечное значение - (((1 - дельта пикета) ^ 2) * дельта)
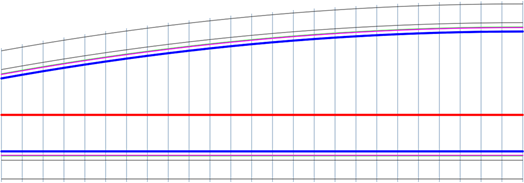
Параболический выход
Параболический переход с расширением, которое возникает в конце перехода и сжимается к его началу.
Для этого перехода используется следующая формула:
начальное значение + ((дельта пикета) ^ 2 * дельта)
Обратный параболический
Для обратного параболического перехода используются следующие формулы.
Для первых 50 % расстояния перехода:
начальное значение + (((дельта пикета * 2) ^ 2) * (дельта / 2))
С 50 % до конца расстояния перехода:
конечное значение - ((((1 - дельта пикета) * 2) ^ 2) * (дельта / 2))