英制单位的渐开线花键计算公式
传递的转矩
![]()
其中:
P | 传递的功率 [lb ft] | |
n | 速度 [min -1 ] |
最小轴直径
1. 轴内径 d h > 0
a) ![]()
b) if d min ≤d h -> d min = 1.1 d h [in]
如果为 else,则使用以下公式来查找最佳直径:
![]()
2. 轴内径 d h = 0
![]()
其中:
d min | 最小轴直径 [inm] | |
d h | 轴内径 [in] | |
T | 转矩 [lb ft] | |
K a | 应用系数 | |
K f | 疲劳寿命系数 | |
S v | 安全系数 | |
τ Al | 许用剪切应力 |
常规计算
用于传递转矩的最小花键长度
1.固定接头:
![]()
2.柔性接头:
![]()
其中:
许用压力
1.固定接头: |
|
2.柔性接头: |
|
其中: |
T | 转矩 [lb ft] | |
K a | 应用系数 | |
K f | 磨损寿命系数 | |
K w | 应用系数 | |
K m | 载荷分布系数 | |
S v | 安全系数 | |
d s | 中径 = (D + d) / 2 [in] | |
D | 槽截面的外部直径 [in] | |
d | 槽截面的内部直径 [in] | |
N | 槽的数量 [-] | |
h | 坡口高度 = (D - d) / 2 [in] | |
s | 倒角 [mm] | |
h st | 接头高度 h st = h - 2 s [in] | |
l f | 有效的键长度 [in] |
强度校核
p min ≤ p Ds
p min ≤ p Dh
其中:
p min | 最小计算 h/2 压力 [psi] | |
p Ds | 轴中的许用压力 [psi] | |
p Dh | 轮毂中的许用压力 [psi] |
外齿根处的剪切应力
对于传动转矩 T,外部花键的齿根直径处的轴中的扭转剪切应力
对于实心轴
![]()
对于空心轴
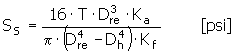
齿中径处的剪切应力
传动转矩 T 的齿节线处的剪切应力
![]()
计算的花键长度:
L f = min {L, Le} [in]
花键齿侧上的抗压应力
花键上的许用抗压应力比齿轮齿上的许用抗压应力要低很多,因为非均布载荷和对齐误差都会导致分载和齿端承载不均等。
对于灵活花键
![]()
对于固定花键
![]()
其中:
计算的花键长度 | L f = min {L, Le} [in] |
齿接合的深度 h h ≅ 0.9 / P [in] | 适用于带有平槽底的花键 |
h ≅ 1 / P [in] | 适用于带有圆角槽底的花键 |
花键上的断裂应力
内部花键可能会因传动载荷的径向分量产生的拉伸应力、离心拉伸应力以及节线处引起齿弯曲的切向力所产生的拉伸应力而断裂。
1.径向载荷拉应力
![]()
其中:内部花键的壁厚 | t w = D oi - D ri [in] |
2.离心拉应力 | |
|
| |
3.梁载荷拉应力 | |
|
|
其中:计算的花键长度 | L f = min {L, L e } [in] |
4.易使外部构件的轮辋断裂的总拉应力
![]()
对齐误差很大的冠状花键
冠状花键可以适应的对齐误差最大为 5 度。冠状花键的载荷能力比同样尺寸的直线花键的载荷能力小很多(二者均在精确对齐的状态下操作)。但是,当存在很大的对齐误差时,冠状花键的载荷能力更大。
可以对冠状外部成员使用美国标准齿形,以使它们能够与标准形状的直线内部成员配合。
齿上的抗压应力
![]()
其中:
冠状齿的曲率半径 | r 2 ≅ F 2 / 8 A [in] |
冠状半径 | r 1 = r 2 tan Φ [in] |
齿接合的深度 h h ≅ 0.9 / P [in] | 适用于带有平槽底的花键 |
h ≅ 1 / P [in] | 适用于带有圆角槽底的花键 |
所用变量的含义