Einstellungen für Gestellanalysen - Registerkarte Berechnung

Berechnungseinstellungen für die Gestellanalyse werden auf alle Simulationen angewendet. Diese Einstellungen werden bei jeder Erstellung einer neuen Simulation verwendet. Sie können die globalen Einstellungen für einzelne Simulationen überschreiben, indem Sie die Simulationseigenschaften ändern.

In diesem Abschnitt werden die Steuerelemente der Registerkarte Berechnung erläutert.

Zugriff:

Multifunktionsleiste: Registerkarte Gestellanalyse Gruppe Einstellungen Einstellungen für Gestellanalysen

DSC-Algorithmus

Der DSC-Algorithmus ermöglicht Ihnen die Berechnung einer Struktur mit Freigaben.

Für alle Träger, für die Sie einen beliebigen Analysetyp definiert haben, und die folgende Freigaben aufweisen:

• Normal
• Unilateral
• Elastisch
• Elastisch und unilateral

werden die folgenden Vorgänge ausgeführt:

• Ein neuer Knoten wird in der Struktur generiert, wenn das Strukturmodell erzeugt wird.

• Das Eingabeelement mit der Freigabe wird geändert. Der neue Knoten ersetzt den alten im Element (der alte Knoten bleibt in anderen Strukturelementen erhalten).

• Zwischen dem alten und dem neuen Knoten erstellt die Gestellanalyse das DSC-Element (Diskontinuität). Betrachten Sie folgende Abbildung:

  

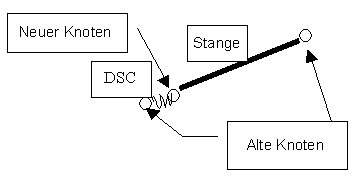
Das DSC-Element besteht aus zwei Knoten, wobei die Knotenkräfte nach der folgenden Formel generiert werden:

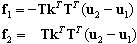
Dabei gilt: k = [ki]; i=1, Ndl ist der Steifigkeitsvektor, der den jeweiligen Freiheitsgraden zugewiesen ist.

Die Steifigkeitsmatrix des Elements weist die folgende Struktur auf:

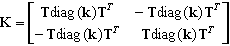
Dabei gilt: T ist die Transformationsmatrix von der lokalen Basis auf die globale Basis, die vom Stabelement übernommen wird, und diag(k) ist die diagonale Matrix aus Vektor k.

Mithilfe der DSC-Elemente können Sie elastische Freigaben für einen Träger definieren.

Lösungsmethode

Wählen Sie eine der folgenden Methoden aus, um das System linearer Gleichungen zu lösen.

• Automatisch - Verwendet einen Satz von Regeln, um die entsprechende Methode auszuwählen.

  • Skyline wird verwendet, wenn die Anzahl der Gleichungen unter 500 liegt.
  • Multithreading wird verwendet, wenn die Anzahl der Gleichungen 5000 überschreitet.
  • Sparse M wird in anderen Fällen verwendet.

• Frontal - Verwendet das gaußsche Eliminationsverfahren.

  • Speichernutzung: gering
  • Festplattennutzung: hoch
  • Geschätzte Geschwindigkeit: langsam
  • Anwendung: bis zu 50000 Gleichungen; lineare und nichtlineare Statik, harmonische Analyse
  • Zusätzliche Anmerkungen: In vielen Fällen können die Zahlen von Knoten und Freiheitsgraden für Gleichungen abgerufen werden, die zu Berechnungsproblemen wie falsch eingeschränkte Strukturen führen.

• Skyline - Verwendet das Cholesky-LDLt-Faktorisierungsverfahren.

  • Speichernutzung: gering
  • Festplattennutzung: hoch
  • Geschätzte Geschwindigkeit: langsam
  • Anwendung: bis zu 50000 Gleichungen; alle Analysetypen
  • Zusätzliche Anmerkungen: In vielen Fällen können die Zahlen von Knoten und Freiheitsgraden für Gleichungen abgerufen werden, die zu Berechnungsproblemen wie falsch eingeschränkte Strukturen führen.

• Sparse - Verwendet das NDM-Verfahren (Nested Dissection Method).

  • Speichernutzung: hoch
  • Festplattennutzung: mittel
  • Geschätzte Geschwindigkeit: mittel/schnell, je nach Wirksamkeit der Neuanordnung
  • Anwendung: 10.000 - 200.000 Gleichungen, alle Analysetypen mit Ausnahme der Modalanalyse zur Erkennung von statischen Kräften
  • Zusätzliche Anmerkungen: Für große 3D-Finite-Elemente-Modelle wie mehrstöckige Gebäude, Wandungsstrukturen und feste Strukturen werden SPDS-Lösungen (Sparse Direct Solvers) empfohlen. Dabei werden falsch konditionierte Strukturen erkannt. Es werden jedoch keine Zahlen von Knoten und Freiheitsgraden für die Gleichungen erfasst, bei denen Berechnungsprobleme auftreten. Dieses Verfahren wird insbesondere für falsch konditionierte Strukturen empfohlen, wenn keine Konvergenz von iterativen Methoden vorliegt.

• Sparse M - Verwendet das MDA-Verfahren (Minimal Degrees Algorithm).

  • Speichernutzung: hoch
  • Festplattennutzung: mittel
  • Geschätzte Geschwindigkeit: mittel/schnell, je nach Wirksamkeit der Neuanordnung
  • Anwendung: 10.000 - 200.000 Gleichungen, alle Analysetypen mit Ausnahme der Modalanalyse zur Erkennung von statischen Kräften
  • Zusätzliche Anmerkungen: Für große 3D-Finite-Elemente-Modelle wie mehrstöckige Gebäude, Wandungsstrukturen und feste Strukturen werden SPDS-Lösungen (Sparse Direct Solvers) empfohlen. Dabei werden falsch konditionierte Strukturen erkannt. Es werden jedoch keine Zahlen von Knoten und Freiheitsgraden für die Gleichungen erfasst, bei denen Berechnungsprobleme auftreten. Dieses Verfahren wird insbesondere für falsch konditionierte Strukturen empfohlen, wenn keine Konvergenz von iterativen Methoden vorliegt.

• Multi-Threading - Verwendet den PARDISO-Solver aus der Intel® Math Kernel Library.

  Möglichkeit zum Berechnen großer Konstruktionsprojekte aufgrund der optimalen Neunummerierung des Gleichungssystems und der Speichernutzung.