Standardberechnungsvorgang

1. Übliche Lösung für kombinierte Belastung

Durch Belastung in der Ebene vertikal zur Ebene der Schweißnaht wird eine Zug- oder Druckspannung σ in der Schweißnaht verursacht.

Normale Spannung, durch die Axialkraft F Z verursacht

Dabei gilt:

	F Z	Axialkraft [N, lb]
	A	Tragender Querschnitt der Schweißnahtgruppe [mm 2, in 2]

Normale Spannung, durch das Biegemoment M verursacht

Dabei gilt:

	u	Konstante
		- für die Berechnung in metrischen Maßeinheiten u = 1000
		- für die Berechnung in englischen Maßeinheiten u = 12
	M	Biegemoment [Nm, lb ft]
	r Y	Abstand des untersuchten Schweißpunkts vom Schwerpunkt der Schweißnahtgruppe in Richtung der Y-Achse [mm, in]
	I	Trägheitsmoment der Schweißnahtgruppe zur neutralen X-Achse [mm 4, in 4]

Gesamte Normalspannung

σ = σ F ± σ M [MPa, psi]

Dabei gilt:

	σ F	Normalspannung, durch die Axialkraft F Z [N, lb] verursacht
	σ M	Normale Spannung, durch das Biegemoment M [mm, in] verursacht

Durch Belastung in der Ebene der Schweißnaht wird eine Scherspannung τ in der Schweißnaht verursacht:

Scherspannung, durch die Schubkraft F Y verursacht

Dabei gilt:

	F Y	Schubkraft [N, lb]
	A	Tragender Querschnitt der Schweißnahtgruppe [mm 2, in 2]

Scherspannung, durch das Drehmoment T verursacht

- X-Komponente der Spannung

- Y-Komponente der Spannung

Dabei gilt:

	u	Konstante
		- für die Berechnung in metrischen Maßeinheiten u = 1000
		- für die Berechnung in englischen Maßeinheiten u = 12
	T	Drehmoment [Nm, lb ft]
	r X	Abstand des untersuchten Schweißpunkts vom Schwerpunkt der Schweißnahtgruppe in Richtung der Y-Achse [mm, in]
	r Y	Abstand des untersuchten Schweißpunkts vom Schwerpunkt der Schweißnahtgruppe in Richtung der Y-Achse [mm, in]
	J	Polares Trägheitsmoment der Schweißnahtgruppe [[mm 4, in 4]

Gesamte Scherspannung

für kreisförmige Schweißnaht:

für andere Schweißnähte:

Dabei gilt:

	τ XT	X-Komponente der Scherspannung, durch das Drehmoment T [MPa, psi] verursacht
	τ Y	Scherspannung, durch die Schubkraft F Y' [MPa, psi] verursacht
	τ YT	Y-Komponente der Scherspannung, durch das Drehmoment T [MPa, psi] verursacht

Resultierende Scherspannung am untersuchten Schweißpunkt

Dabei gilt:

	σ	Gesamte Normalspannung [MPa, psi]
	τ	Gesamte Scherspannung [MPa, psi]

2. Belastung durch Biegekraft F Y

Zu Berechnungszwecken kann die Biegekraft durch eine Kombination aus der Schubkraft F Y, die auf die Ebene der Schweißnaht wirkt, und dem Biegemoment M, das auf die Ebene vertikal zur Ebene der Schweißnaht wirkt, ersetzt werden. Daraufhin kann die Spannung in der Schweißnaht mit der zuvor erwähnten Vorgehensweise berechnet werden.

Das Biegemoment ist durch eine Formel definiert:

Dabei gilt:

	F Y	Schubkraft [N, lb]
	e	Hebelarm der Biegekraft [mm, in]
	u	Konstante
		- für die Berechnung in metrischen Maßeinheiten u = 1000
		- für die Berechnung in englischen Maßeinheiten u = 12

3. Belastung mit allgemeiner Kraft F Y

Zu Berechnungszwecken kann die allgemeine Kraft F durch eine Kombination aus der Schubkraft F Y, die auf die Ebene der Schweißnaht mit der Axialkraft F Z wirkt, und dem Biegemoment M, das auf die Ebene vertikal zur Ebene der Schweißnaht wirkt, ersetzt werden. Daraufhin kann die Spannung in der Schweißnaht für die so definierte Belastung mit der oben erwähnten Vorgehensweise berechnet werden.

Die einzelnen Komponenten der Belastung sind in Formeln definiert:

- Biegemoment

- Axialkraft

F Z = F cos φ [N, lb]

- Schubkraft

F Y = F cos φ [N, lb]

Dabei gilt:

	F	Einwirkende Kraft [N, lb]
	r F	Kraftarm, der mit dem Schwerpunkt der Schweißnahtgruppe zusammenhängt [mm, in]
	u	Konstante
		- für die Berechnung in metrischen Maßeinheiten u = 1000
		- für die Berechnung in englischen Maßeinheiten u = 12
	φ	Richtungswinkel der einwirkenden Kraft [°]

Spannungsvergleichsmethode

1. Übliche Lösung für kombinierte Belastung

Verglichen mit der Standardberechnungsmethode wird bei der Methode der Referenzspannungen (Spannungsvergleichsmethode) ein anderer Ansatz für die Berechnung von Spannungen verwendet, die durch die auf der Ebene vertikal zur Ebene der Schweißnaht wirkende Axialkraft oder das entsprechende Biegemoment verursacht werden. Im Allgemeinen weist die Spannung in Kehlnähten normale und tangentiale Komponenten auf. Die Spannungsvergleichsmethode beruht auf der Tatsache, dass die Schubfestigkeit von Schweißmetall geringer als die Zugfestigkeit ist. Um die Berechnung zu vereinfachen, werden bei Schweißverbindungen nur Scherspannungen überprüft. Die Berechnungsmethode entspricht jedoch der Standardberechnungsmethode. Die zur Berechnung verwendeten Formeln sind ebenfalls ähnlich.

Belastung auf der Ebene vertikal zur Ebene der Schweißnaht:

Scherspannung, durch die Axialkraft F Z verursacht

Dabei gilt:

	F Z	Axialkraft [N, lb]
	A	Tragender Querschnitt der Schweißnahtgruppe [mm 2, in 2]

Scherspannung, durch das Biegemoment M verursacht

Dabei gilt:

	M	Biegemoment [Nm, lb ft]
	r Y	Abstand des untersuchten Schweißpunkts vom Schwerpunkt der Schweißnahtgruppe in Richtung der Y-Achse [mm, in]
	u	Konstante
		- für die Berechnung in metrischen Maßeinheiten u = 1000
		- für die Berechnung in englischen Maßeinheiten u = 12
	I	Trägheitsmoment der Schweißnahtgruppe zur neutralen X-Achse [mm 4, in 4]

Belastung auf der Ebene der Schweißnaht:

Scherspannung, durch die Schubkraft F Y verursacht

Dabei gilt:

	F Y	Schubkraft [N, lb]
	A	Tragender Querschnitt der Schweißnahtgruppe [mm 2, in 2]

Scherspannung, durch Drehmoment T verursacht

- Spannung X-Komponente

- Spannung Y-Komponente

Dabei gilt:

	T	Drehmoment [Nm, lb ft]
	u	Konstante
		- für die Berechnung in metrischen Maßeinheiten u = 1000
		- für die Berechnung in englischen Maßeinheiten u = 12
	r Y	Abstand des untersuchten Schweißpunkts vom Schwerpunkt der Schweißnahtgruppe in Richtung der Y-Achse [mm, in]
	r X	Abstand des untersuchten Schweißpunkts vom Schwerpunkt der Schweißnahtgruppe in Richtung der X-Achse [mm, in]
	J	Polares Trägheitsmoment der Schweißnahtgruppe [[mm 4, in 4]

Gesamte Scherspannung am untersuchten Schweißpunkt

Dabei gilt:

	τ XT	X-Komponente der Scherspannung, durch das Drehmoment T [MPa, psi] verursacht
	τ Y	Scherspannung, durch die Schubkraft F Y' [MPa, psi] verursacht
	τ YT	Y-Komponente der Scherspannung, durch das Drehmoment T [MPa, psi] verursacht
	τ Z	Scherspannung, durch die Schubkraft F Z [MPa, psi] verursacht
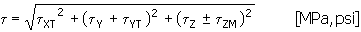
	τ ZM	Scherspannung, durch das Biegemoment M [MPa, psi] verursacht

2. Berechnung der Referenzspannung σ s

Die Referenzspannung wird anhand der Formel aus den berechneten Teilspannungen ermittelt.

Wobei für die X-Komponente der Spannung, die am untersuchten Schweißpunkt vertikal zur Nahtrichtung wirkt, die Formel α X = α 3 angewendet wird. Im umgekehrten Fall wird α X = α 4 angewendet. Dasselbe gilt für die Y-Komponente der Spannung, die vertikal zur Nahtrichtung wirkt, das heißt α Y = α 3 oder α Y = α 4.

	τ XT	X-Komponente der Scherspannung, durch das Drehmoment T [MPa, psi] verursacht
	τ Y	Scherspannung, durch die Schubkraft F Y [MPa, psi] verursacht
	τ YT	Y-Komponente der Scherspannung, durch das Drehmoment T [MPa, psi] verursacht
	τ Z	Scherspannung, durch die Schubkraft F Z [MPa, psi] verursacht
	τ ZM	Scherspannung, durch das Biegemoment M [MPa, psi] verursacht
	α 3	Konversionskoeffizient der Schweißnaht für die Kehlendnaht [-]
	α 4	Konversionskoeffizient der Schweißnaht für die Kehlendnaht [-]