Parámetros de análisis de la estructura: ficha Solucionador

La configuración del solucionador de análisis de estructura se aplica a todas las simulaciones. Siempre que se inicia una nueva simulación, se usan estas preferencias. Puede anular la configuración global modificando las propiedades en las distintas simulaciones.

En esta sección se describen los controles de la ficha Solucionador.

Acceso:

Cinta de opciones: ficha Análisis de estructura panel Parámetros Parámetros de análisis de la estructura .

Algoritmo dsc

El algoritmo dsc permite calcular una estructura con liberaciones.

Para cualquier viga, en la que se haya definido cualquier tipo de análisis, con las siguientes liberaciones:

• Normal
• Unilateral
• Elástica
• Elástica y unilateral

Se efectúan las siguientes operaciones:

• Se genera un nuevo nodo en la estructura cuando se genera el modelo de estructura.

• Se modifica el elemento de entrada con la liberación. El nuevo nodo reemplaza al anterior en el elemento (el nodo anterior permanece en el resto de elementos de la estructura).

• Entre el nuevo nodo y el anterior, Análisis de estructura crea el elemento DSC (discontinuidad). Observe la siguiente imagen:

  

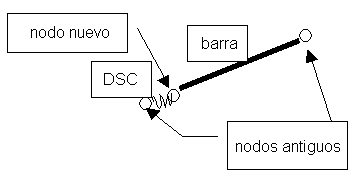
El elemento dsc es un elemento de dos nodos, en el que las fueras de nodo se generan de acuerdo a la siguiente fórmula:

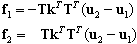
donde k = [ki]; i=1, Ndl es el vector de rigidez asignado a los grados de libertad particulares.

La matriz de rigidez del elemento tiene la siguiente estructura:

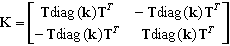
donde T es la matriz de transformación desde la base local a la global, heredada del elemento de barra, y diag(k) es la matriz diagonal creada a partir del vector k.

El uso de elementos dsc permite definir liberaciones elásticas en una viga.

Método de resolución

Seleccione uno de los siguientes métodos para resolver el sistema de ecuaciones lineales.

• Automático: emplea un conjunto de reglas para seleccionar el método adecuado.

  • Skyline se utiliza si el número de ecuaciones es inferior a 500.
  • La opción Multiproceso se utiliza si el número de ecuaciones es superior a 5000.
  • Sparse M se utiliza en otros casos.

• Frontal: utiliza el método de eliminación de Gauss.

  • Uso de memoria: bajo
  • Uso del disco: alto
  • Estimación de velocidad: lenta
  • Aplicación: hasta 50 000 ecuaciones; estática lineal y no lineal, análisis armónico
  • Comentarios adicionales: en muchos casos permite obtener el número de nodos y grados de libertad en ecuaciones, lo que conduce a problemas de cálculo tales como estructuras restringidas incorrectamente.

• Skyline: utiliza el método de factorización Cholesky LDLt.

  • Uso de memoria: bajo
  • Uso del disco: alto
  • Estimación de velocidad: lenta
  • Aplicación: hasta 50 000 ecuaciones; todos los tipos de análisis
  • Comentarios adicionales: en muchos casos permite obtener el número de nodos y grados de libertad en ecuaciones, lo que conduce a problemas de cálculo tales como estructuras restringidas incorrectamente.

• Disperso: utiliza el método de secciones anidadas (NDM).

  • Uso de memoria: alto
  • Uso del disco: medio
  • Estimación de velocidad: media/rápida, según la efectividad de la reorganización
  • Aplicación: 10 000-200 000 ecuaciones; todos los tipos de análisis excepto el análisis modal que reconozca fuerzas estáticas
  • Notas adicionales: se recomienda el uso de solucionadores directos de Disperso (SPDS) para modelos de elementos finitos 3D de gran tamaño como, por ejemplo, edificios de varias plantas, estructuras de carcasa y estructuras macizas. Detecta de forma incorrecta las estructuras condicionadas, pero no lleva a obtener el número de nodos y grados de libertad de las ecuaciones donde se produce un problema de cálculo. Se recomienda especialmente para las estructuras condicionadas de forma incorrecta si no hay convergencia de los métodos de iteración.

• Sparse M: utiliza el algoritmo de potencia mínima (MDA).

  • Uso de memoria: alto
  • Uso del disco: medio
  • Estimación de velocidad: media/rápida, según la efectividad de la reorganización
  • Aplicación: 10 000-200 000 ecuaciones; todos los tipos de análisis excepto el análisis modal que reconozca fuerzas estáticas
  • Notas adicionales: se recomienda el uso de solucionadores directos de Disperso (SPDS) para modelos de elementos finitos 3D de gran tamaño como, por ejemplo, edificios de varias plantas, estructuras de carcasa y estructuras macizas. Detecta de forma incorrecta las estructuras condicionadas, pero no lleva a obtener el número de nodos y grados de libertad de las ecuaciones donde se produce un problema de cálculo. Se recomienda especialmente para las estructuras condicionadas de forma incorrecta si no hay convergencia de los métodos de iteración.

• Multiproceso: utiliza el solucionador PARDISO de la biblioteca Intel® Math Kernel.

  Posibilidad de calcular proyectos de estructuras grandes debido a la óptima renumeración del sistema de ecuaciones y el uso de memoria.