A propos des définitions de clothoïde

Du point de vue de sa relation aux autres tangentes et courbes, chaque clothoïde est soit une courbe intérieure, soit une courbe extérieure.

Les deux paramètres les plus fréquemment utilisés par les ingénieurs dans la conception d’une clothoïde sont la longueur de clothoïde (L) et le rayon de courbe circulaire (R). Le paramètre R correspond au rayon de courbure à l’une des extrémités de la clothoïde. Vous pouvez différencier les rayons de début et de fin de la clothoïde en les appelant R₁ et R₂.

L'illustration suivante présente les différents paramètres d'une clothoïde :

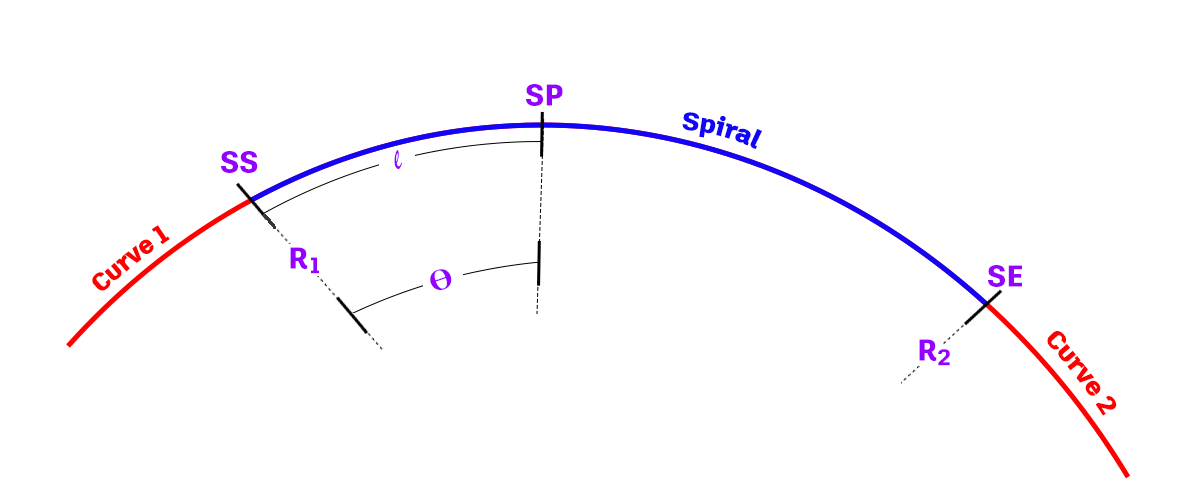
Paramètre de clothoïde	Description
R₁	Rayon de la courbe 1.
R₂	Rayon de la courbe 2.
SS	Position du début de la clothoïde.
SE	Position de la fin de la clothoïde.
SP	Point de la clothoïde au niveau de la longueur de l’arc l.
Θ	Angle central au point de la clothoïde au niveau de la longueur de l’arc l.
l	Longueur de l’arc depuis le début de la clothoïde le long de celle-ci.
L	Longueur totale de l’arc de clothoïde entre le début et la fin de celle-ci.

Clothoïde composée

Les clothoïdes composées fournissent une transition entre deux courbes circulaires de rayons différents. Il existe deux types de clothoïdes : les simples et les composées. Les clothoïdes composées sont des courbes constituées de deux clothoïdes simples. Elles sont donc en deux parties, chacune constituée d’une clothoïde simple, qui se rejoignent de façon tangente. Cela garantit la continuité de la fonction de courbure et fournit un moyen d’introduire une transition progressive dans le dévers.

Clothoïde

Parmi les différents types de clothoïde pris en charge par Autodesk Civil 3D, Clothoïde est le plus fréquemment utilisé. La clothoïde est utilisée dans le monde entier dans la conception des routes ainsi que des voies ferrées.

Initialement étudiée par le mathématicien suisse Leonard Euler, la fonction de courbure de la clothoïde est une fonction linéaire prévoyant une courbure nulle (0) là où la clothoïde rencontre la tangente. La courbure augmente ensuite de manière linéaire jusqu'à ce qu'elle soit égale à la courbe adjacente au point où la clothoïde et la courbe se rencontrent.

À la différence d’une courbe simple, elle maintient également la continuité de la courbure locale, qui devient de plus en plus importante avec l’accroissement de la vitesse.

Formule

Les clothoïdes peuvent être exprimées par les formules suivantes :

Où :

Θ= Angle central au point de la clothoïde au niveau de la longueur de l’arc l.
l = Longueur de l’arc le long de la courbe.

Veuillez vous référer au schéma ci-dessus.

Planéité de la clothoïde :

Angle total sous-tendu par la clothoïde :

Distance de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

Distance de décalage de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

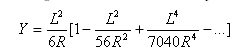
Clothoïde de Bloss

La clothoïde de Bloss peut servir de transition à la place des clothoïdes classiques. Cette clothoïde offre un avantage sur la clothoïde dans la mesure où le décalage P est plus petit, ce qui produit une transition plus longue, avec une extension de clothoïde plus importante (k). Ce facteur est important pour la conception de rails.

Formule

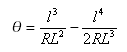
Les clothoïdes de Bloss peuvent être calculées à l'aide de l'expression suivante :

Autres expressions clés :

Distance de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

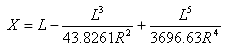
Distance de décalage de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

Courbes sinusoïdales

Ces courbes représentent une trajectoire de courbure constante et s'appliquent à des déflexions de tangente pouvant être comprises entre 0 et 90 degrés. Néanmoins, les courbes sinusoïdales sont rarement utilisées car elles sont plus raides que les clothoïdes et il est par ailleurs difficile de les présenter sous forme de tableau et de les délimiter.

Formule

Les courbes sinusoïdales peuvent être calculées à l'aide de l'expression suivante :

Où :

Θ= Angle central au point de la clothoïde au niveau de la longueur de l’arc i.
l = Longueur de l’arc le long de la courbe.

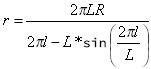
Veuillez vous référer au schéma ci-dessus.

Où r est le rayon de courbure en un point donné.

Courbe de type tangente décroissante de demi-longueur d'onde sinusoïdale

Cette forme d'équation est fréquemment utilisée au Japon pour la conception de voies ferrées. Cette courbe est utile dans les cas où vous avez besoin d'une transition efficace dans la modification de la courbure pour de faibles angles de déflexion (compte tenu de la dynamique des véhicules).

Formule

Les courbes de type tangente décroissante de demi-longueur d'onde sinusoïdale peuvent être calculées à l'aide de l'expression suivante :

où et x correspondent à la distance comprise entre le début de la courbe et un point de celle-ci, mesurée sur la tangente initiale (étendue) ; X correspond à la valeur X totale à l’extrémité de la courbe de transition.

Autres expressions clés :

Distance de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

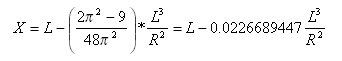
Distance de décalage de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

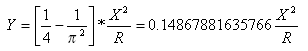
Paraboles cubiques

Les paraboles cubiques convergent moins rapidement que les clothoïdes cubiques, c'est la raison pour laquelle elles sont couramment utilisées lors de la conception de rails et d'autoroutes.

Formule

Rayon minimum de parabole cubique

Le rayon à un point donné d'une parabole cubique correspond à :

Où : Θ = Angle central au point de la clothoïde au niveau de la longueur de l’arc .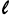

Veuillez vous référer au schéma ci-dessus.

Une parabole cubique atteint une valeur r minimale à :

Donc

Le rayon d’une parabole cubique diminue de l’infini à à 24 degrés, 5 minutes et 41 secondes, puis augmente à nouveau. Par conséquent, les paraboles cubiques sont inutiles pour les déflexions supérieures à 24 degrés.

Cubique (Japon)

Cette transition a été développée pour répondre aux exigences rencontrées au Japon. Des approximations de la clothoïde ont été développées pour les cas où il est nécessaire d'utiliser un petit angle de déflexion ou un grand rayon. L'une de ces approximations, utilisée pour la conception au Japon, est la parabole cubique (JP).

Formule

Les paraboles cubiques (JP) peuvent être calculées à l'aide de l'expression suivante :

Où X = distance de tangente au point clothoïde-courbe depuis le point tangente-clothoïde

L'expression suivante de la formule est également correcte :

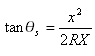
Où est l’angle central de la clothoïde (i1 et i2 dans l’illustration)

Autres expressions clés :

Distance de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

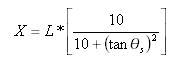
Distance de décalage de tangente au point clothoïde-courbe depuis le point tangente-clothoïde :

Parabole cubique NSW

Il s'agit d'un type de parabole cubique modifiée qui permet de respecter les normes de Nouvelle Galle du Sud (Australie).

Formule

La parabole cubique NSW (New South Wales) peut être exprimée comme suit :

Où :

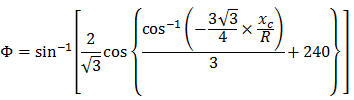
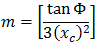
Φ = angle entre la dernière ligne radiale sur R et la ligne perpendiculaire à la tangente initiale
R = rayon de la courbure
X_c = total X de la clothoïde
Y_c = total Y de la clothoïde

Clothoïdes biquadratiques (Schramm)

Les clothoïdes biquadratiques (Schramm) possèdent de faibles valeurs d'accélération verticale. Elles possèdent deux paraboles du second degré dont les rayons varient en fonction de la longueur de la courbe (l)..

Formule de courbe simple

Courbure de la première parabole :

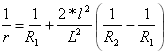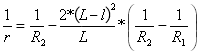pour