Paramètres d’analyse de l’ossature - Onglet Résolution

Les paramètres de résolution de l’analyse de l’ossature s’appliquent à toutes les simulations. Ils sont utilisés dès qu'une nouvelle simulation démarre. Ces paramètres peuvent varier selon la simulation. Pour en changer, modifiez les propriétés de la simulation.

La section suivante décrit les options de l’onglet Résolution.

Mode d’accès :

Sur le ruban, cliquez sur l’onglet Analyse de l’ossature

groupe de fonctions Paramètres

Paramètres d’analyse de l’ossature

Valeurs de résolution par défaut
	Algorithme DSC (relâchements de poutres)	Cliquez pour activer l’élément de discontinuité pendant les calculs d’une structure lorsque des relâchements sont définis.
Résultats
	Points de la poutre	Spécifiez le nombre de points de poutre qui sont calculés au cours de la résolution.

Algorithme DSC

L’algorithme DSC permet de calculer une structure avec des relâchements.

Remarque : les relâchements spécifient le degré de liberté de relâchement au début et à la fin des éléments de poutre.

Pour toute poutre pour lequel vous avez défini un type d’analyse, avec l’un des relâchements suivants :

Standard
Unilatéral
Elastique
Elastique et unilatéral

Les opérations suivantes sont réalisées :

Un nouveau noeud est généré dans la structure lorsque le modèle est généré.
L'élément en entrée présentant le relâchement est modifié. Le nouveau noeud remplace l'ancien dans l'élément (l'ancien noeud reste dans les éléments de l'autre structure).
Entre l’ancien et le nouveau nœud, l’analyse de l’ossature crée l’élément DSC (discontinuité). Reportez-vous à l’image ci-dessous :

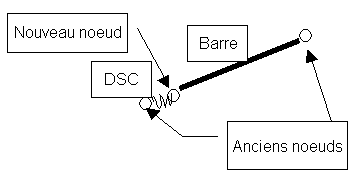
L’élément DSC est un élément à deux nœuds, où les forces nodales sont générées selon la formule suivante :

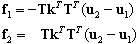
où k = [ki]; i=1, Ndl est le vecteur des rigidités affecté aux degrés de liberté respectifs.

La matrice de rigidité a la structure suivante :

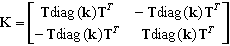
T étant la matrice de transformation de la base locale vers la base globale, héritée de la barre, et diag(k) étant la matrice diagonale générée à partir du vecteur k.

L'utilisation des éléments DSC permet de définir les relâchements élastiques dans une poutre.

Méthode de résolution

Sélectionnez l’une des méthodes suivantes pour résoudre le système d’équations linéaires.

Automatique : repose sur un jeu de règles pour sélectionner la méthode appropriée.
- Skyline : si le nombre d’équations est inférieur à 500.
- Multi-thread : si le nombre d’équations dépasse 5 000.
- Sparse M : dans les autres cas.
Frontal : utilise la méthode d’élimination de Gauss.
- Utilisation de la mémoire : faible
- Utilisation du disque : importante
- Vitesse estimée : lente
- Application : jusqu’à 50 000 équations ; analyse harmonique, statique linéaire et non linéaire.
- Remarques supplémentaires : la méthode permet souvent de trouver les nœuds et les degrés de relâchement d'équations causant des problèmes de calcul, par exemple des structures aux restrictions incorrectes.
Skyline : utilise la méthode de factorisation de Cholesky LDLt.
- Utilisation de la mémoire : faible
- Utilisation du disque : importante
- Vitesse estimée : lente
- Application : jusqu’à 50 000 équations. Tous types d’analyses
- Remarques supplémentaires : la méthode permet souvent de trouver les nœuds et les degrés de relâchement d'équations causant des problèmes de calcul, par exemple des structures aux restrictions incorrectes.
Sparse : utilise la méthode des dissections emboîtées (NDM).
- Utilisation de la mémoire : importante
- Utilisation du disque : moyenne
- Vitesse estimée : moyenne/rapide, selon l’efficacité de la réorganisation.
- Application : de 10 000 à 200 000 équations. Tous types d'analyse, à l'exception de l'analyse modale tenant compte des forces statique.
- Remarques complémentaires : les solveurs directs (SPDS) sont recommandés pour les modèles d'éléments finis en 3D, tels que : bâtiments multi-étages, structures solides et en coques.. Les solveurs, s'ils détectent les structures incorrectes, ne permettent pas de trouver les nœuds et les degrés de relâchement d'équations faisant l'objet d'un problème de calcul. Ils sont particulièrement indiqués pour les structures mal préparées, notamment en cas d'absence de méthodes itératives convergentes.
Sparse M : utilise le degré minimum approché (MDA).
- Utilisation de la mémoire : importante
- Utilisation du disque : moyenne
- Vitesse estimée : moyenne/rapide, selon l’efficacité de la réorganisation.
- Application : de 10 000 à 200 000 équations. Tous types d'analyse, à l'exception de l'analyse modale tenant compte des forces statique.
- Remarques complémentaires : les solveurs directs (SPDS) sont recommandés pour les modèles d'éléments finis en 3D, tels que : bâtiments multi-étages, structures solides et en coques.. Les solveurs, s'ils détectent les structures incorrectes, ne permettent pas de trouver les nœuds et les degrés de relâchement d'équations faisant l'objet d'un problème de calcul. Ils sont particulièrement indiqués pour les structures mal préparées, notamment en cas d'absence de méthodes itératives convergentes.
Multi-thread : utilise le solveur PARDISO de la bibliothèque Intel® Math Kernel.

Possibilité d'effectuer des calculs portant sur des projets de structure volumineux grâce à une meilleure renumérotation du système d'équations et utilisation de la mémoire plus performante.