Calculs de poinçonnement - description

Calcul de la surface critique et du périmètre critique

La forme de la surface critique dépend de la géométrie de l’appui ou de son chapiteau, de l’angle d’inclinaison de la surface cisaillée et de la position par rapport aux bords et aux coins de la dalle. La forme et les dimensions de la surface critique sont définies par la norme mais, pour chaque norme, les calculs consistent à calculer la surface sollicitée par la force de poinçonnement. Dans le calcul, les bords de zone de la dalle et des ouvertures sont pris en compte. Le tableau affiche la longueur du périmètre critique u. Attention : l'influence des ouvertures sur la longueur du périmètre critique est prise en compte par le logiciel.

A = u * d

où :

A - surface critique

u - longueur du périmètre critique

d - hauteur efficace de la section de la dalle.

Calcul des forces de poinçonnement limites ou des efforts limites

Dans cette étape, le logiciel calcule les valeurs maximales réglementaires admissibles de la force de poinçonnement ou des contraintes maximales transférées par une section béton. La force limite (maximale) est le produit de la surface critique et des contraintes réglementaires admissibles.

Q_adm = τ * A

où :

Q_adm - Force de poinçonnement admissible

τ - Contrainte admissible

A - Curface critique

Calcul des forces de poinçonnement ou des contraintes résultant d’un impact externe

Chacune des normes détermine la manière dont une force ou une contrainte provoquée par un impact externe doit être reçue sur la surface de poinçonnement. Dans le cas le plus simple, les calculs se limitent à la multiplication de la force de poinçonnement par le coefficient approprié, dans les calculs les plus complexes, il est nécessaire de calculer les contraintes avec la prise compte de l’action des moments. Le tableau affiche la valeur de l'effort dimensionnant Q, obtenue à partir de la formule suivante :

Q = τ * A

τ = V / A

(pour la norme ACI)

où :

Q - effort dimensionnant de calcul

τ - contrainte sur la surface critique

V – force de poinçonnement maximale

Mx, My, V - moments de flexion et force dans le centre de gravité de la surface critique

Jx, Jy - Moments d’inertie de la surface critique par rapport aux axes passant par son centre de gravité

γ _x , γ _y, c _x , c _y - Paramètres dépendant de la géométrie de la surface critique [ACI 318 11.12.2.2].

Pour l’Eurocode EN 1992-1-1, sur la base du point 6.4.3, paragraphe 3, les calculs incluent l’excentricité de la force. L’excentricité est prise en compte sur la base d’un facteur défini par l’Eurocode comme coefficient β dans l’équation (6.39). RSA à chaque fois inclut l’excentricité biaxiale. De ce fait, l’équation (6.39) est étendue et comporte deux parties indépendantes pour M_x/W_1x et M_y/W_1y.

Vérification de la condition de résistance

Cette opération consiste à comparer les contraintes ou forces provoquées par l’impact externe avec des valeurs limites. Trois états sont possibles :

• Si les contraintes calculées sont inférieures aux contraintes admissibles dans la section béton, l'armature n’est pas exigée
• Si les contraintes sont supérieures aux contraintes admissibles pour la section béton et qu’elles sont inférieures aux contraintes admissibles, l'armature est exigée
• Si les contraintes sont supérieures aux contraintes admissibles, cela signifie que la section de la dalle est trop faible.

Si l'armature n’est pas exigée ou que la section de la dalle est trop faible, les résultats sont présentés sous la forme de la force de poinçonnement minimale (pour les calculs basés sur les contraintes, la force est calculée à la base des contraintes multipliées par l’aire de surface du poinçonnement) et à la base du rapport effort admissible / effort de calcul. Si une armature est nécessaire, le logiciel effectue les calculs d’armature nécessaire.

Calcul d’armature nécessaire

Si les contraintes sont supérieures aux contraintes admissibles d’une section béton et, simultanément, inférieures aux contraintes admissibles, le calcul d’armature de poinçonnement est nécessaire. Les calculs sont effectués conformément aux conditions réglementaires des normes pour l'armature des barres. Le logiciel présente : la section nécessaire et la portée de la zone pour laquelle l'armature est exigée. Les valeurs en question sont présentées dans le tableau, dans l’onglet Poinçonnement, de plus, la valeur de la force de poinçonnement est présentée (pour les calculs basés sur les contraintes, la force est calculée à la base des contraintes multipliées par l’aire de surface de poinçonnement) à la base du rapport effort admissible / effort de calcul. L’étendue de la zone d'armature est représentée sur les dessins; le tableau présente les paramètres suivants :

L1, L2 – armatures à partir du centre du poteau dans les deux directions perpendiculaires.

u – longueur du périmètre de la zone d'armature suivant les conditions réglementaires.

A – zone d'armatures totale à répartir de façon uniforme autour du poteau au sein de la zone d'armatures définie par les longueurs L1 et L2.

n x ϕ - nombre et diamètre des barres, calculés en fonction de la surface totale et des paramètres des options de poinçonnement.

Remarque :

Pour l’Eurocode EN 1992-1-1 point 6.4.3, trois états sont possibles.

• Lorsque v_Ed < v_Rd,c l’armature de poinçonnement n’est pas nécessaire pour transférer les forces d’action.
• Lorsque v_Ed > v_Rd,c et v_Ed < v_Rd,max une armature de poinçonnement est nécessaire.
• Dans ce dernier cas où v_Ed > v_Rd,max la résistance au cisaillement est insuffisante pour transférer les forces d’action.

D’après le point 6.4.3, paragraphe 3, les calculs incluent l’excentricité de la force. Les valeurs Q et Q_adm sont présentées dans le tableau de la boîte de dialogue et la note représente les valeurs de calcul des forces d’action et de résistance, y compris les effets de l’excentricité. L’excentricité est prise en compte sur la base d’un facteur défini par l’Eurocode comme coefficient β dans l’équation (6.39). RSA à chaque fois inclut l’excentricité biaxiale. De ce fait, l’équation (6.39) est étendue et comporte deux parties indépendantes pour M_x/W_1x et M_y/W_1y. Q_adm dépend de l’état de conception et représente la valeur admissible en fonction de v_Rd,c, v_Rd,s orv_Rd,max.

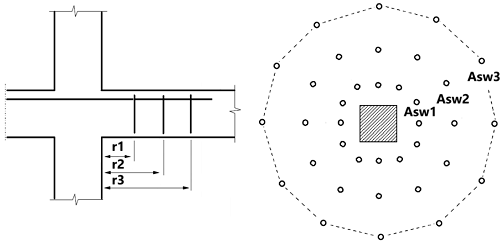
Lorsque v_Ed > v_Rd,c et v_Ed < v_Rd,max l’armature de cisaillement A_sw est calculée sur la base de l’équation (6.52). Le périmètre le plus à l’extérieur de l’armature de cisaillement u_out sur la base des exigences de l’Eurocode est également calculé. On suppose que l’espacement maximal des liaisons de cisaillement dans la direction tangentielle s_t est égal à 2*d. Pour chaque périmètre, l’armature est la même, sauf dans les situations où l’équation A _sw,min (6.11) est importante. Dans ce cas, les valeurs r, u et A _sw sont présentées dans le tableau de la boîte de dialogue et de la note.

r_i représentent les rayons des périmètres

u_i correspond aux longueurs des périmètres

A_sw donne la valeur de l’armature de cisaillement basée sur l’équation (6.52)

n x ϕ comme ci-dessus

Les valeurs suivantesde r_i u_i A_sw représentent des valeurs comme sur l’image ci-dessous :

Remarque : Pour la norme britannique BS, il est possible de spécifier plusieurs zones d’armature en fonction des exigences (les zones d’armature peuvent être superposées) ; par conséquent, dans les zones successives, la distribution des barres concerne seulement la partie des barres calculées qui reste après la soustraction des barres qui appartiennent aussi à la zone précédente.