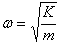Casi teorici per la convalida delle simulazioni
Una delle fasi di un processo di progettazione affidabile è rappresentato dalla convalida. Per convalidare un progetto è spesso consigliabile utilizzare alcuni casi teorici semplici e affidabili con cui eseguire il confronto. Di seguito sono riportati alcuni di questi casi.
Nei casi seguenti vengono descritte le equazioni e i presupposti utilizzati per ottenere la convalida dell'output di una simulazione.
Spostamento, caso massa-molla
Si tratta di un semplice caso di convalida di massa e molla.

Legge di Newton:
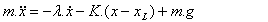 (1)
(1)
Con:
| | Valore numerico: |
|---|
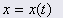 : posizione, basata sul tempo t : posizione, basata sul tempo t | |
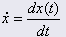 : velocità : velocità | |
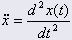 : accelerazione : accelerazione | |
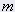 = massa del corpo in kg = massa del corpo in kg | 10 |
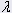 = smorzamento della molla in N.s/m = smorzamento della molla in N.s/m | 20 |
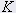 = rigidità della molla in N/m = rigidità della molla in N/m | 15000 |
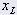 = lunghezza libera della molla in m = lunghezza libera della molla in m | 0.3 |
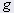 = gravità in m/s2 = gravità in m/s2 | 9.81 |
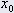 posizione iniziale in m posizione iniziale in m | 0.33 |
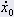 = velocità iniziale in m/s = velocità iniziale in m/s | 0.0 |
(1)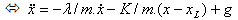 |
con 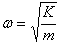 |
| | 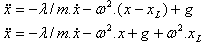 (2) (2)
|
Una soluzione per questa equazione differenziale è la seguente: |
| | 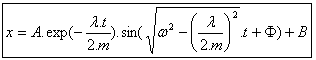 (3) (3)
|
Una soluzione specifica, quando il sistema si è stabilizzato, è per 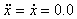 e x = B. e x = B. |
Quindi (2) 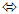 | 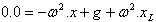 |
| | 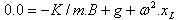
|
| | 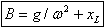 (4) (4)
|
Le condizioni iniziali forniscono il valore di A e 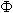 : : |
per t = 0,0, (3)  | 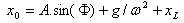 |
| | 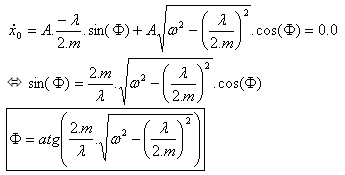 (5) (5)
|
| | e |
| |  (6) (6)
|
Al termine, (4) e (6) riportati in (3) forniscono l'equazione dello spostamento: |
| 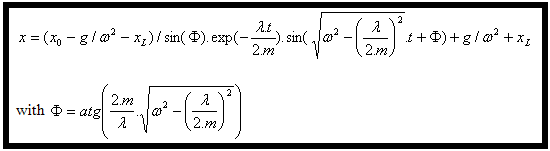
|
Questa equazione è stata quindi programmata in Excel e i risultati, confrontati con quelli prodotti da Simulazione dinamica, sono stati identici. |
| |
Posizione e velocità, caso pistone-manovella
Lo scopo di questo caso di convalida è quello di verificare la posizione e la velocità di un meccanismo costituito da un pistone e un albero a gomito quando l'output della simulazione dinamica e le equazioni teoriche indicano lo stesso risultato.
Valori noti: la "corsa" o la distanza del perno di banco dell'albero a gomito dal suo centro di rotazione e la lunghezza della biella compresa tra il perno di banco del cuscinetto principale e la connessione a spina del pistone.
Diagramma
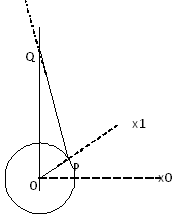
Definizione | R = length(OP) = corsa dell'albero a gomito L = length(PQ) = lunghezza della biella |
| | |
Velocità del punto Q in relazione al sistema di coordinate assoluto R0 = (x0, y0) |
| | // posizione di Q in R0 |
| | // velocità di Q in R0 |
| con: 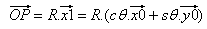
|
| e: 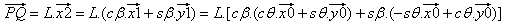
|
| |
con: 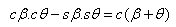 |
e; 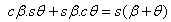 |
quindi: 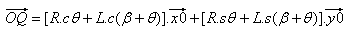 |
Il punto Q si trova sull'asse y0 e il componente x0 è 0,0: |
| |
| |
| Infine, utilizzando (1): | |
| | |
L'equazione (1) fornisce 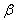 : che non è lineare in base al tempo; quindi : che non è lineare in base al tempo; quindi 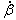 non è una constante e non è una constante e 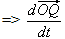 non è una funzione periodica semplice. non è una funzione periodica semplice. |
(1) 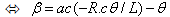 |
e 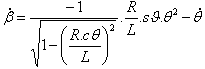 |
Utilizzando MS Excel e i valori numerici (L=0,125m, R=0,06m e 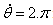 rad/s), viene calcolata la posizione e la velocità del punto Q come indicato di seguito: rad/s), viene calcolata la posizione e la velocità del punto Q come indicato di seguito: |
Posizione: | |
| |
Velocità: | |
| |
Risultato: le curve nella simulazione dinamica sono identiche a quelle prodotte dalle equazioni teoriche.

![]() (1)
(1)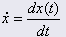 : velocità
: velocità![]()