土木工学では、さまざまな摺り付け曲線を使用して、接線間、円曲線間、さらには曲率の異なる 2 つの曲線間に円曲線と横断勾配摺り付けを漸次的に挿入します。
他の接線や曲線との関係で、各緩和曲線は、始点側緩和曲線または終点側緩和曲線のいずれかになります。
エンジニアが緩和曲線の設計と設定で最も一般的に使用する 2 つのパラメータは、L (緩和曲線の長さ)と R です。R パラメータは、緩和曲線の一方の端における曲率半径です。R1 と R2 を使用して、緩和曲線の始点と終点の半径を区別できます。
次の図に、緩和曲線のさまざまなパラメータを示します。
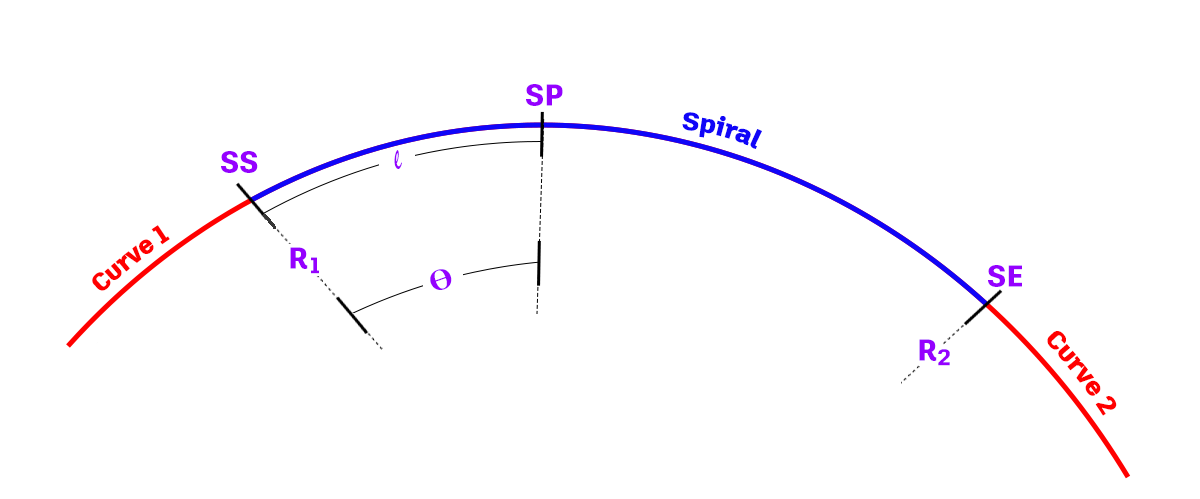
| 緩和曲線パラメータ | 説明 |
| R1 | 曲率半径 1。 |
| R2 | 曲率半径 2。 |
| SS<so>SS | 緩和曲線の開始位置。 |
| SE | 緩和曲線の終了位置。 |
| SP | 円弧の長さ l の緩和曲線ポイント。 |
| Θ | 円弧の長さ l の緩和曲線ポイントの中心角度。 |
| l | 緩和曲線の開始位置から緩和曲線に沿った円弧の長さ。 |
| L | 緩和曲線の開始位置と終了位置の間の緩和曲線の円弧の全長。 |
卵形曲線
卵形曲線は、半径が異なる 2 つの円弧間の摺り付けを提供します。緩和曲線には、単純と卵形の 2 つのタイプがあります。卵型曲線は、2 つの基本型緩和曲線で構成されます。これには 2 つのスパンが含まれ、それぞれが基本型緩和曲線であり、隣接する緩和曲線と接線が連続的に結合します。基本型緩和曲線と同様、これにより、曲率関数の連続が可能となり、横断勾配摺り付けにスムーズな摺り付けを導入できます。
クロソイド曲線
Autodesk Civil 3D ではいくつかの緩和曲線タイプがサポートされていますが、最もよく使用される緩和曲線タイプはクロソイド曲線です。クロソイド曲線は、高速道路と鉄道の両方の設計で世界的に使用されています。
スイスの数学者 Leonard Euler によって最初に研究がなされたクロソイド曲線は、曲率が一次関数であり、緩和曲線と接線との接点では長さの関数として曲率は 0 (ゼロ)度です。曲率は、緩和曲線が隣接する曲線との接点でその曲線と等しくなるまで直線的に増加します。
単曲線とは異なり、ローカル曲率の連続も維持します。これは、高速走行する車両にとってますます重要になっています。
公式
クロソイド曲線は、次の式で表すことができます。 
- Θ= 円弧の長さ l の緩和曲線ポイントの中心角度。
- l = 曲線に沿った円弧の長さ。
緩和曲線の平坦度 
緩和曲線によって限定される角度 
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線距離
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線オフセット距離
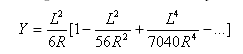
ブロス緩和曲線
クロソイドを使用する代わりに、ブロス緩和曲線を摺り付けとして使用できます。この緩和曲線がクロソイドより有利な点は、シフト P が小さいため、摺り付けが長く、緩和曲線拡張(K)が大きくなるところです。これは、線路の設計においては重要視される性質です。
公式
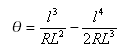
他の式:
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線距離
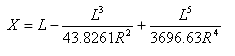
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線オフセット距離
正弦曲線
この曲線は、曲率が一定のコースを表し、接線の偏角が 0 度から 90 度の摺り付けに利用できます。ただし、正弦曲線は、通常の緩和曲線よりも勾配が急で、作表や杭による区画が困難なため、あまり広く使用されていません。
公式
- Θ= 円弧の長さ i の緩和曲線ポイントの中心角度。
- l = 曲線に沿った円弧の長さ。
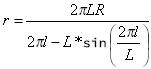
r は任意のポイントの曲率半径です。
サイン半波長逓減曲線
この計算式は、日本の線路の設計でよく使用されます。この曲線は、(動力性能に関して)小さい偏角で曲率の変更の効果的な推移が必要な場合に便利です。
公式
サイン半波長逓減曲線は、次のように表すことができます。
と x は曲線上の始点から任意のポイントまでの距離で、(延長された) 初期接線に沿って計測されます。X は摺り付け曲線の終点での合計 X です。
他の式:
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線距離
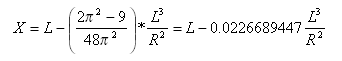
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線オフセット距離
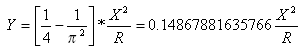
3 次曲線
3 次曲線は、収束が 3 次緩和曲線ほど急速ではなく、鉄道や高速道路の設計で一般的に使用されています。
公式
3 次曲線の最小半径
説明: Θ= 円弧長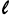 
の緩和曲線ポイントの中心角度。
上の図を参照先として参照してください。
3 次曲線は、次の場合に r が最小になります。
したがって、
3 次曲線の曲率半径は、24 度 5 分 41 秒で無限から に減少し、それ以降は再び増加します。このため、偏角が 24 度より大きくなると、3 次曲線は有用でなくなります。
3 次曲線(JP)
この摺り付けは、日本での要件に合わせて開発されたものです。小さい偏角または大きい半径に対応することが必要な状況で使用するために、クロソイドに似た曲線がいくつか開発されました。これらのうち、日本で設計用に使用されているのが 3 次曲線(JP)です。
公式
3 次曲線(JP)は次のように表すことができます。
X = 接線-緩和曲線ポイントから緩和曲線-曲線ポイントまでの接線距離。
この公式は次のように表すこともできます。
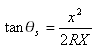
は緩和曲線の中心角(図中の i1 と i2)です。
他の式:
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線距離
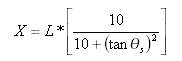
接線-緩和曲線ポイントからの緩和曲線-曲線ポイントでの接線オフセット距離
NSW 3 次曲線
これは、オーストラリア ニューサウスウェールズ州標準の要件を満たすように修正された 3 次曲線(放物線)のタイプです。
公式
NSW 3 次曲線は次のように表すことができます。
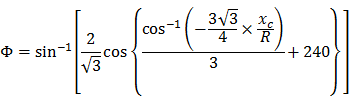
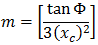
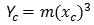
- Φ = R における最終半径線と、初期接線に対する垂線との間の角度
- R = 曲率半径
- Xc = 任意の緩和曲線の合計 X
- Yc = 任意の緩和曲線の合計 Y
双 2 次式(Schramm)緩和曲線
双 2 次式(Schramm)緩和曲線は、垂直加速度の値が小さい曲線です。これらの曲線には、曲線の長さの関数(l)によって半径が異なる 2 次曲線が 2 つあります。
単純な曲線の公式
最初の曲線の曲率:
の場合 
2 番目の曲線の曲率
の場合 
この曲線は、摺り付け曲線のユーザ定義の長さ(L)で指定します。
複心曲線の公式
最初の曲線の曲率:
の場合 
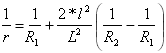
2 番目の曲線の曲率
の場合 