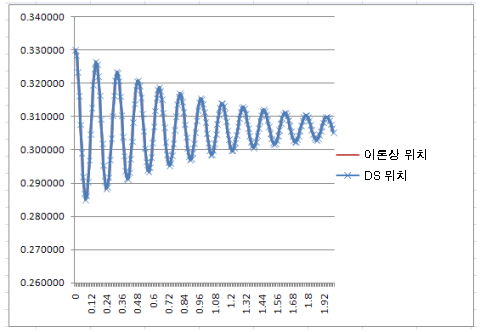
시뮬레이션 확인을 위한 이론상의 경우
합리적인 설계 프로세스의 단계 중 하나는 확인입니다. 설계를 확인하려면 신뢰할 수 있는 단순한 이론상의 경우를 사용하여 측정해보는 것이 좋습니다. 다음이 그러한 경우입니다.
시뮬레이션 출력의 확인을 얻기 위해 사용된 방정식과 가정이 각 경우에 대해 설명되어 있습니다.
변위, 질량-스프링의 경우
단순한 질량 및 스프링 확인의 경우

뉴턴의 법칙
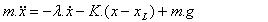 (1)
(1)
포함:
| | 수치 값: |
|---|
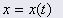 : 위치, 시간 기반(t) : 위치, 시간 기반(t) | |
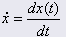 : 속도 : 속도 | |
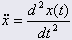 : 가속도 : 가속도 | |
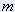 = 본체 질량(kg) = 본체 질량(kg) | 10 |
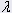 = 스프링 댐핑(N.s/m) = 스프링 댐핑(N.s/m) | 20 |
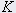 = 스프링 강성(N/m) = 스프링 강성(N/m) | 15000 |
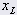 = 스프링 자유 길이(m) = 스프링 자유 길이(m) | 0.3 |
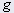 = 중력(m/s2) = 중력(m/s2) | 9.81 |
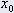 초기 위치(m) 초기 위치(m) | 0.33 |
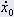 초기 속도(m/s) 초기 속도(m/s) | 0.0 |
(1)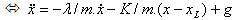 |
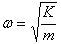 포함 포함
|
| | 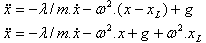 (2) (2)
|
이렇게 차이가 있는 방정식에 대한 해는 다음과 같습니다. |
| | 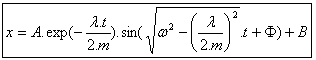 (3) (3)
|
시스템이 안정적일 때 특별한 해는 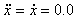 및 x = B에 대한 것입니다. 및 x = B에 대한 것입니다. |
그런 다음 (2) 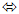 | 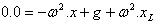 |
| | 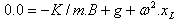
|
| | 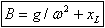 (4) (4)
|
초기 조건은 값 A 및 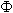 제공: 제공: |
t = 0.0, (3) 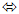 | 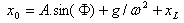 |
| | 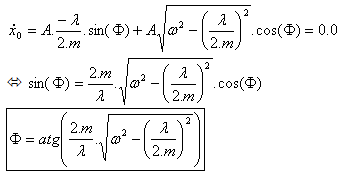 (5) (5)
|
| | AND |
| |  (6) (6)
|
마지막으로 (3)에서 보고된 (4)와 (6)은 변위의 방정식을 제공합니다. |
| 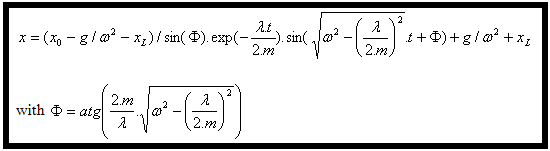
|
이 방정식은 Excel에서 프로그래밍했고 그 결과를 다이나믹 시뮬레이션에서 작성한 결과와 비교했으며, 두 결과는 동일했습니다. |
| |
위치 및 속도, 크랭크-피스톤의 경우
이번 확인의 목적은 다이나믹 시뮬레이션의 출력을 이론상 방정식과 비교해서 결과가 같은 경우 크랭크샤프트와 피스톤 매커니즘에서 위치와 속도를 확인하는 것입니다.
알려진 값: 크랭크샤프트의 회전 중심으로부터 크랭크샤프트 저널의 "throw" 또는 거리, 주 베어링 저널과 피스톤 핀 접합 간 연결 로드의 길이.
다이어그램
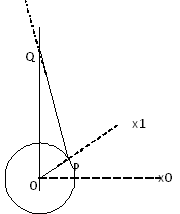
정의 | R = 길이(OP) = 크랭크샤프트 throw L = 길이(PQ) = 연결 로드 길이 |
| | |
절대 좌표계 R0 = (x0, y0)과 관련된 점 Q의 속도 |
| | // R0에서 Q의 위치 |
| | // R0에서 Q의 속도 |
| 다음을 사용: 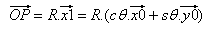
|
| 및: 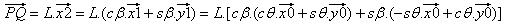
|
| |
다음을 사용: 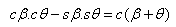 |
및: 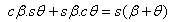 |
그런 다음: 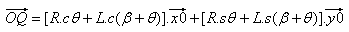 |
점 Q는 y0 축에 있으며 x0 구성요소는 0.0입니다. |
| |
| |
| 마지막으로 (1) 사용: | |
| | |
방정식 (1) 결과  : 이것은 시간 기반의 선형이 아니므로 : 이것은 시간 기반의 선형이 아니므로 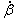 은 상수가 아니며 은 상수가 아니며 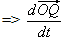 은 단순한 주기 함수가 아닙니다. 은 단순한 주기 함수가 아닙니다. |
(1) 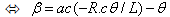 |
및 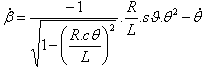 |
MS Excel 및 수치 값(L=0.125m, R=0.06m 및 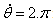 rad/s)를 사용하여 다음과 같이 점 Q의 위치 및 속도를 계산합니다. rad/s)를 사용하여 다음과 같이 점 Q의 위치 및 속도를 계산합니다. |
위치: | |
| |
속도: | |
| |
결과: 다이나믹 시뮬레이션의 곡선은 이론적 방정식으로 산출한 곡선과 동일합니다.

![]() (1)
(1)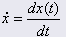 : 속도
: 속도![]()
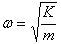 포함
포함