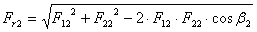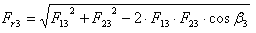동기식 벨트 강도 비율 계산
| 
| 각 풀리의 경우 |
F 2 - F 1 + F p = 0 |
| 
|
| 
|
| 
|
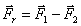
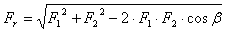
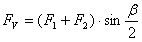
연동 풀리의 경우
| 
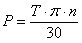
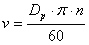
| v ≤ v max |
| 
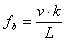
| f b ≤ f max |
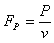
F c = mv 2
F Tmax = k 1 F p + F c
F 1 = F tmax
F 2 = F 1 - F p
개별 연계 풀리 및 아이들러의 경우
풀리의 i 지수
F Pi = P xi F p
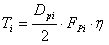
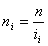
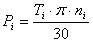
F 1i = F 2i-1
F 2i = F 1i + F p i
설명:
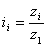동기식 풀리의 경우
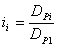플랫 풀리의 경우
전체 벨트 연동의 경우
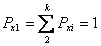
필요한 벨트 장착 장력은 다음과 같이 연동 풀리의 힘에 따라 결정됩니다.
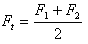
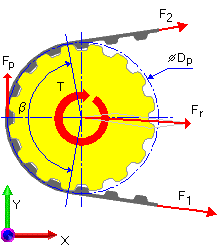
아이들러를 사용한 전동의 예
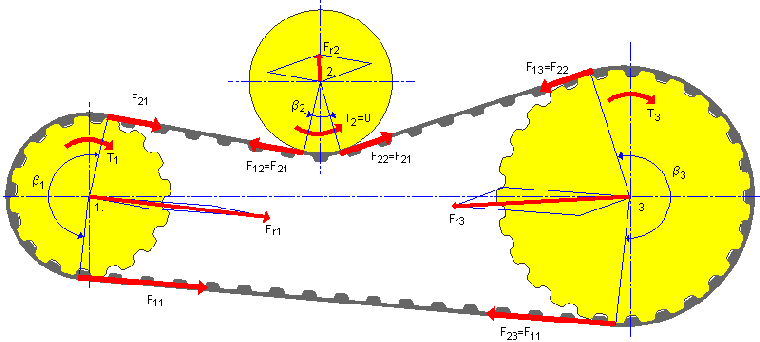
연동 풀리 | 플랫 아이들러 | 연계 풀리 |
P x1 = 1 | P x2 = 0 | P x3 = 1 |
| 
| 
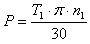
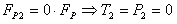
| F P3 = P x3 F p |
| 
| 
| 
|
| 
| 
| 
|
| 
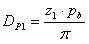
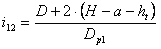
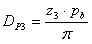
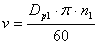
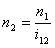
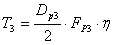
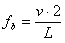
| F 12 = F 21 |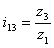 
|
| 
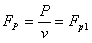
| F 22 = F 12 + F p2 = F 12 |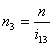 
|
F c = m v 2 |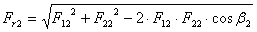 
| 
|
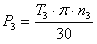
F Tmax = k 1 F p + F C | - | F 13 = F 22 |
F 11 = F Tmax | - | F 23 = F 13 + F p3 = F 11 |
F 21 = F 11 - F p | - |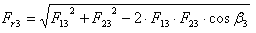 
|
| 
| - | - |
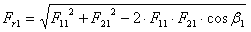
사용된 변수의 의미:
F p | 유효 인장 [N] |
F 1 | 주어진 풀리의 입력 면 벨트 장력 [N] |
F 2 | 주어진 풀리의 출력 면 벨트 장력 [N] |
z | 주어진 풀리의 톱니 수/벨트 톱니 수 [-] |
| β | 접촉 호/톱니면 경사 각도 [도] |
P | 전달할 동력 [W] |
P R | 주어진 전동 배치에 대한 벨트 동력비 [W] |
c L | 서비스 계수 [-] |
| β | 접촉 호 [도] |
T | 주어진 풀리에 작용하는 토크 [Nm] |
n | 주어진 풀리의 속도 [rpm] |
D p | 피치 풀리 지름 [m] |
v | 벨트 속도 [m/s] |
k | 벨트 전동 내 풀리 수 [-] |
L | 벨트 피치 길이 [m] |
P | 전달할 동력 [W] |
m | 주어진 폭에 대한 고유 벨트 가중치 [Kg/m] |
k 1 | 벨트 인장 계수 [-] |
F p | 유효 인장 [N] |
F c | 원심력 [N] |
F t | 최소 벨트 장착 장력 [N] |
P xi | 주어진 풀리의 동력비 [-] |
D pi | 피치 풀리 지름 [m] |
i | 주어진 풀리의 전동비(속도비) [-] |
T i | 주어진 풀리에 작용하는 토크 [Nm] |
| η | 효율 [-] |
p b | 원형 피치 [m] |
D | 공칭 플랫 풀리 지름 [m] |
H | 벨트 높이 [m] |
h T | 벨트 톱니 높이 [m] |
a | 피치 선 간격띄우기 [m] |
참고: i = 풀리 지수
계산 기본 사항