Tolerancja — wzory obliczeń

Porada: W przypadku obliczeń analizy tolerancji 1D warto rozważyć użycie dodatku Autodesk® Inventor® Tolerance Analysis. Inventor Tolerance Analysis zawiera bogaty zestaw narzędzi, które pozwalają lepiej zrozumieć wpływ mechanicznego dopasowania i działania w oparciu o skumulowaną zmienność wymiarową.

Aby uzyskać więcej informacji, zobacz temat Definiowanie sumowań tolerancji.

Podstawowe równania dla zamkniętych łańcuchów wymiarów liniowych można wyprowadzić z poniższej ilustracji.

a = 32 ± 1,5 mm, b = 8 ± 1 mm

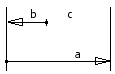
Zwiększanie/zmniejszanie elementów

Jeżeli element narastający rośnie, element zamykający także rośnie. Jeśli element malejący rośnie, element zamykający maleje, jeśli inne elementy łańcucha pozostają stałe.

Element zamykający:	1. c = a - b
Górny wymiar graniczny zamykającego elementu:	2. c_maks.= a_maks.- b_min.
Dolny wymiar graniczny zamykającego elementu:	3. c_min.= a_min.- b_maks.
Tolerancja elementu zamykającego (odjęcie równania 3 od równania 2)	4. c_maks.- c_min.= a_maks.- a_min.- (b_min.- b_maks.)
Tak jak	5. T_c= T_a+ T_b

Uwaga: Tolerancja elementu zamykającego jest sumą tolerancji wszystkich elementów zamkniętych łańcuchem wymiarowania

Na ogół tolerancje łańcucha liniowego spełniają poniższe równanie.

Podobnie równania 2 i 3 można zapisać w ogólnej postaci.

Górny wymiar graniczny elementu zamykającego równy jest różnicy sumy górnych wymiarów granicznych powiększanych elementów i sumy dolnych wymiarów granicznych elementów zmniejszanych.

Dolny wymiar graniczny elementu zamykającego równy jest różnicy sumy dolnych wymiarów granicznych powiększanych elementów i sumy górnych wymiarów granicznych elementów zmniejszanych.

Wymiar nominalny elementu zamykającego można wyrazić używając równania 1, jak w poniższym równaniu.

Górna granica odchyłki elementu zamykającego:

Dolna granica odchyłki elementu zamykającego: