Krzywe zmęczenia w połączeniach spawanych
Do określania wytrzymałości zmęczeniowej połączeń spawanych można używać różnych typów krzywych zmęczeniowych. Poniżej znajdują się równania pojedynczych krzywych naprężenia normalnego i ścinającego.
1. Metoda wirtualnego naprężenia średniego
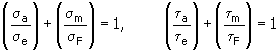
gdzie:
| | σ a , τ a | amplituda normalnego (ścinającego) naprężenia [MPa, psi]. |
| | σ e , τ e | wytrzymałość zmęczeniowa przy stałej wytrzymałości [MPa, psi] |
| | σ m , τ m | średnie naprężenie cyklu [MPa, psi]. |
| | σ F , τ F | wirtualne naprężenie średnie [MPa, psi] |
| | Ψ | współczynnik zwężenia diagramu Haigha [-] |
| | | zależy od materiału połączenia (zalecane wartości) dla rozciągania i zginania Ψ<0,15–0,3> |
| | | - dla ścinania <0,1–0,25>. |
2. Zmodyfikowana metoda Godmana
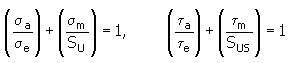
gdzie:
| | σ a , τ a | amplituda normalnego (ścinającego) naprężenia [MPa, psi]. |
| | σ e , τ e | wytrzymałość zmęczeniowa przy stałej wytrzymałości [MPa, psi] |
| | σ m , τ m | średnie naprężenie cyklu [MPa, psi]. |
| | S U | wytrzymałość na rozciąganie [MPa, psi] |
| | S US | wytrzymałość na ścinanie [MPa, psi] |
| | | natomiast S US ≈ 0,8 S U |
3. Metoda kwadratowa (eliptyczna)
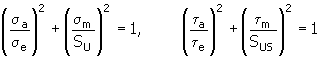
Wyjaśnienie zmiennych znajduje się w elemencie 2 - Zmodyfikowana metoda Godmana
4. Metoda paraboliczna Gerbera
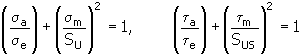
Wyjaśnienie zmiennych znajduje się w elemencie 2 - Zmodyfikowana metoda Godmana
5. Metoda Keccecioglu, Chestera i Dodge'a

gdzie:
| | σ a , τ a | amplituda normalnego (ścinającego) naprężenia [MPa, psi]. |
| | σ e , τ e | wytrzymałość zmęczeniowa przy stałej wytrzymałości [MPa, psi] |
| | σ m , τ m | średnie naprężenie cyklu [MPa, psi]. |
| | S U | wytrzymałość na rozciąganie [MPa, psi] |
| | S US | wytrzymałość na ścinanie [MPa, psi] |
| | | natomiast S US ≈ 0,8 S U |
| | a | wykładnik zależny od materiału połączenia [-] |
| | | zalecane wartości a <2,6–2,75> |
6. Metoda Bagcia
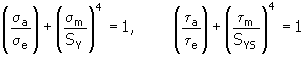
gdzie:
| | σ a , τ a | amplituda normalnego (ścinającego) naprężenia [MPa, psi]. |
| | σ e , τ e | wytrzymałość zmęczeniowa przy stałej wytrzymałości [MPa, psi] |
| | σ m , τ m | średnie naprężenie cyklu [MPa, psi]. |
| | S Y | granica plastyczności przy rozciąganiu [MPa, psi] |
| | S YS | granica plastyczności przy ścinaniu [MPa, psi] |
| | | natomiast S YS ≈ 0,577 S Y |
7. Metoda Soderberga
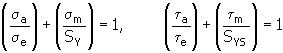
wyjaśnienie zmiennych znajduje się w elemencie 6 - Metoda Bagcia
![]()
![]()
![]()
![]()
![]()
![]()
![]()