Znormalizowany proces obliczenia

1. Wspólne rozwiązanie dla obciążenia połączonego

Obciążenie w płaszczyźnie prostopadłej do płaszczyzny spoiny wywołuje naprężenie rozciągające lub ściskające w spoinie.

Naprężenie normalne wywołane siłą osiową F Z

gdzie:

	F Z	siła osiowa [N, funt].
	A	przekrój nośny grupy spoin [mm 2 , cal 2 ].

Naprężenie normalne wywołane momentem zginającym M

gdzie:

	u	stałe
		- dla obliczeń przy jednostkach metrycznych u = 1000
		- dla obliczeń przy jednostkach angielskich u = 12
	M	moment zginający [Nm, funt stopa]
	r Y	odległość śledzonego punktu spawalniczego od punktu ciężkości grupy spawalniczej w kierunku osi y [mm, cal]
	I	moment bezwładności grupy spoin względem neutralnej osi x [mm 4 , cal 4 ]

Całkowite naprężenie normalne

σ = σ F ± σ M [MPa, psi]

gdzie:

	σ F	naprężenie normalne wywołane siłą osiową F Z [N, funt]
	σ M	naprężenie normalne wywołane momentem zginającym M [mm, cal]

Naprężenie w płaszczyźnie spoiny wywołuje naprężenie ścinające w spoinie:

Naprężenie ścinające wywołane siłą ścinającą F Y

gdzie:

	F Y	siła ścinająca [N, funt]
	A	przekrój nośny grupy spoin [mm 2 , cal 2 ]

Naprężenie ścinające wywołane momentem obrotowym T

- składowa x naprężenia

- składowa y naprężenia

gdzie:

	u	stałe
		- dla obliczeń przy jednostkach metrycznych u = 1000
		- dla obliczeń przy jednostkach angielskich u = 12
	T	moment obrotowy [Nm, funt stopa]
	r X	odległość badanego punktu spoiny do środka ciężkości grupy spoin w kierunku osi Y [mm, cal]
	r Y	odległość badanego punktu spoiny do środka ciężkości grupy spoin w kierunku osi Y [mm, cal]
	J	biegunowy moment bezwładności grupy spoin [mm 4 , cal 4 ]

Całkowite naprężenie ścinające

dla spoin okrągłych:

dla pozostałych spoin:

gdzie:

	τ XT	składowa x naprężenia ścinającego wywołanego momentem obrotowym T [MPa, psi]
	τ Y	naprężenie ścinające wywołane siłą ścinającą F Y ' [MPa, psi]
	τ YT	składowa y naprężenia ścinającego wywołanego momentem obrotowym T [MPa, psi]

Wypadkowe naprężenie ścinające w badanym punkcie spoiny

gdzie:

	σ	całkowite naprężenie normalne [MPa, psi]
	τ	całkowite naprężenie ścinające [MPa, psi]

2. Wczytywanie z siłą zginającą F Y

Dla celów obliczeniowych siłę zginającą można zastąpić połączeniem siły ścinania F Y działającej w płaszczyźnie spoiny i momentu zginającego M działającego w płaszczyźnie prostopadłej do płaszczyzny spoiny. Następnie naprężenie w spoinie można obliczyć korzystając z wyżej opisanej procedury.

Moment zginający jest zdefiniowany formułą:

gdzie:

	F Y	siła ścinająca [N, funt]
	e	ramię siły zginającej [mm, cal]
	u	stałe
		- dla obliczeń przy jednostkach metrycznych u = 1000
		- dla obliczeń przy jednostkach angielskich u = 12

3. Obciążenie z siłą ogólną F Y

Dla celów obliczeniowych siłę ogólną F można zastąpić połączeniem siły ścinania F Y działającej w płaszczyźnie spoiny z siłą osiową F Z i momentu zginającego M działającego w płaszczyźnie prostopadłej do płaszczyzny spoiny. Następnie naprężenie w spoinie dla tak zdefiniowanego obciążenia można obliczyć korzystając z wyżej opisanej procedury.

Poszczególne składowe obciążenia są zdefiniowane przez formuły:

- moment zginający

- siła osiowa

F Z = F cos φ [N, lb]

- siła ścinająca

F Y = F cos φ [N, funt]

gdzie:

	F	działająca siła [N, funt]
	r F	ramię siły związane z środkiem ciężkości grupy spawalniczej [mm, cal]
	u	stałe
		- dla obliczeń przy jednostkach metrycznych u = 1000
		- dla obliczeń przy jednostkach angielskich u = 12
	φ	kąt kierunku siły oddziaływującej [°]

Metoda naprężeń porównawczych

1. Wspólne rozwiązanie dla obciążenia połączonego

W porównaniu ze znormalizowaną metodą obliczeń, metoda naprężeń porównawczych daje dostęp do innego sposobu obliczania naprężeń wywołanych siłą osiową lub momentem zginającym działającym w płaszczyźnie prostopadłej do płaszczyzny spoiny. Ogólnie naprężenie w spoinach kątowych posiada składowe normalną i styczną. Metoda naprężeń porównawczych jest oparta na fakcie, że wytrzymałość na ścinanie metalu spoiny jest mniejsza niż wytrzymałość na rozciąganie. Aby uprościć obliczenia, połączenia spawane są kontrolowane tylko dla naprężenia ścinającego. Ale metoda obliczeń jest ta sama, co w standardowej metodzie obliczeń. Używane formuły obliczeń są również podobne.

Obciążenie w płaszczyźnie prostopadłej do płaszczyzny spawania:

Naprężenie ścinające wywołane siłą osiową F Z

gdzie:

	F Z	siła osiowa [N, funt].
	A	przekrój nośny grupy spoin [mm 2 , cal 2 ].

Naprężenie ścinające wywołane momentem zginającym M

gdzie:

	M	moment zginający [Nm, funt stopa]
	r Y	odległość śledzonego punktu spawalniczego od punktu ciężkości grupy spawalniczej w kierunku osi y [mm, cal]
	u	stałe
		- dla obliczeń przy jednostkach metrycznych u = 1000
		- dla obliczeń przy jednostkach angielskich u = 12
	I	moment bezwładności grupy spoin względem neutralnej osi x [mm 4 , cal 4 ]

Obciążenie w płaszczyźnie spawania:

Naprężenie ścinające wywołane siłą ścinającą F Y

gdzie:

	F Y	siła ścinająca [N, funt]
	A	przekrój nośny grupy spoin [mm 2 , cal 2 ]

Naprężenie ścinające wywołane momentem obrotowym T

- składowa x naprężenia

- składowa y naprężenia

gdzie:

	T	moment obrotowy [Nm, funt stopa]
	u	stałe
		- dla obliczeń przy jednostkach metrycznych u = 1000
		- dla obliczeń przy jednostkach angielskich u = 12
	r Y	odległość badanego punktu spoiny do środka ciężkości grupy spoin w kierunku osi Y [mm, cal]
	r X	odległość badanego punktu spoiny do środka ciężkości grupy spoin w kierunku osi X [mm, cal]
	J	biegunowy moment bezwładności grupy spoin [mm 4 , cal 4 ]

Całkowite naprężenie ścinające w punkcie śledzonym spoiny

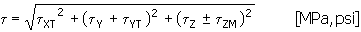
gdzie:

	τ XT	składowa x naprężenia ścinającego wywołanego momentem obrotowym T [MPa, psi]
	τ Y	naprężenie ścinające wywołane siłą ścinającą F Y ' [MPa, psi]
	τ YT	składowa y naprężenia ścinającego wywołanego momentem obrotowym T [MPa, psi]
	τ Z	naprężenie ścinające wywołane siłą ścinającą F Z [MPa, psi]
	τ ZM	Naprężenie ścinające wywołane momentem zginającym M [MPa, psi]

2. Obliczenia naprężeń porównawczych σ s

Naprężenie porównawcze jest wyznaczone z obliczonych naprężeń częściowych zgodnie z formułą.

gdzie dla składowej x naprężenia, poruszającej się w punkcie śledzonym spoiny, prostopadłej do kierunku spoiny jest zastosowany wzór α X = α 3. W przeciwnym wypadku α X = α 4 . Tak samo jest dla składowej y naprężenia działającego prostopadle do kierunku spoiny, które jest wyrażone α Y = α 3 lub α Y = α 4.

	τ XT	składowa x naprężenia ścinającego wywołanego momentem obrotowym T [MPa, psi]
	τ Y	naprężenie ścinające wywołane siłą ścinającą F Y [MPa, psi]
	τ YT	składowa y naprężenia ścinającego wywołanego momentem obrotowym T [MPa, psi]
	τ Z	naprężenie ścinające wywołane siłą ścinającą F Z [MPa, psi]
	τ ZM	Naprężenie ścinające wywołane momentem zginającym M [MPa, psi]
	α 3	współczynnik konwersji połączenia spawanego dla spoiny kątowej czołowej [-]
	α 4	współczynnik konwersji połączenia spawanego dla spoiny kątowej czołowej [-]