Obliczenia na przebicie — opis

Wyliczanie powierzchni krytycznej i obwodu krytycznego

Kształt powierzchni krytycznej zależny jest od geometrii podpory lub jej głowicy, kąta nachylenia powierzchni ścinanej oraz położenia względem krawędzi i naroży płyty. Kształt i rozmiary powierzchni krytycznej są ściśle określone w normie, ale dla każdej normy obliczenia polegają na wyznaczeniu powierzchni, na której oddziałuje siła przebijająca. W obliczeniu tej strefy są uwzględniane krawędzie płyty oraz otworów. W tabeli wyświetlana jest długość obwodu krytycznego u. Wpływ otworów na długość obwodu krytycznego jest uwzględniany w programie

A = u * d

gdzie:

A — powierzchnia krytyczna

u — długość obwodu krytycznego

d — wysokość użyteczna przekroju płyty.

Wyliczenie granicznych sił przebijających lub naprężeń granicznych

Na tym etapie obliczeń są wyznaczane maksymalne dopuszczone przez normę wartości siły przebijającej lub naprężeń maksymalnych, które może przenieść przekrój betonowy. Siła graniczna (maksymalna) jest iloczynem powierzchni krytycznej i naprężeń dopuszczonych przez normę.

Q_adm = τ * A

gdzie:

Q_adm — dopuszczalna siła przebijająca

τ — dopuszczalne naprężenie

A — powierzchnia krytyczna.

Wyliczenie sił przebijających lub naprężeń wynikających z oddziaływań zewnętrznych

Każda z norm określa, w jaki sposób siła lub naprężenia wynikające z oddziaływań zewnętrznych powinny zostać odebrane na powierzchni przebicia. W najprostszym przypadku obliczenia sprowadzają się do przemnożenia siły przebijającej przez odpowiedni współczynnik, w najbardziej skomplikowanych wymagane są obliczenia naprężeń z uwzględnieniem działających momentów. W tabeli wyświetlana jest wartość obliczeniowej siły wymiarującej Q, otrzymanej z poniższego wzoru.

Q = τ * A

τ = V / A

(dla normy ACI)

gdzie:

Q — obliczeniowa siła wymiarująca

τ — naprężenie na powierzchni krytycznej

V — maksymalna siła przebijająca

Mx, My, V — momenty zginające i siła w środku ciężkości powierzchni krytycznej

Jx, Jy — momenty bezwładności powierzchni krytycznej względem osi przechodzących przez jej środek ciężkości

γ _x , γ _y, c _x , c _y — parametry w zależności od geometrii powierzchni krytycznej [ACI 318 11.12.2.2].

W przypadku normy Eurocode EN 1992-1-1 na podstawie punktu 6.4.3(3) obliczenia uwzględniają mimośród siły. Mimośród jest uwzględniany na podstawie współczynnika zdefiniowanego przez Eurocode jako współczynnik β w równaniu (6.39). RSA w każdym przypadku uwzględnia mimośród dwuosiowy. Z tego powodu równanie (6.39) jest rozszerzane i ma dwie niezależne części dla M_x/W_1x i M_y/W_1y.

Sprawdzenie warunku nośności

Polega to na porównaniu naprężeń lub sił oddziaływań zewnętrznych z wartościami granicznymi. Możliwe są trzy stany:

• Jeżeli naprężenia wyliczone są mniejsze od dopuszczalnych dla przekroju betonowego, zbrojenie nie jest wymagane
• Jeżeli naprężenia są większe od dopuszczalnych dla przekroju betonowego, a jednocześnie mniejsze od dopuszczalnych, to zbrojenie jest wymagane
• jeżeli naprężenia są większe od dopuszczalnych, to oznacza to, że przekrój płyty jest za mały.

W przypadku gdy zbrojenie nie jest wymagane lub gdy przekrój płyty jest za mały, wyniki prezentowane są w postaci maksymalnej siły przebijającej (w przypadku obliczeń opartych na naprężeniach siła jest wyliczana z naprężeń przemnożonych przez powierzchnię przebicia) i stosunku siły dopuszczalnej do sprowadzonej siły działającej. Gdy wymagane jest zbrojenie, to w programie wykonywane są obliczenia wymaganego zbrojenia.

Obliczenie wymaganego zbrojenia

Jeżeli naprężenia są większe od dopuszczalnych dla przekroju betonowego, a jednocześnie mniejsze od dopuszczalnych, to wymagane jest obliczane zbrojenie na przebicie. Obliczenia są prowadzone zgodnie z wytycznymi norm dla zbrojenia prętami. W programie prezentowane są: wymagana powierzchnia zbrojenia oraz zasięg strefy, w której wymagane jest zbrojenie. Wartości te są prezentowane w tabeli na karcie Przebicie, dodatkowo jest prezentowana wartość siły przebijającej (w przypadku obliczeń opartych na naprężeniach siła jest wyliczana z naprężeń przemnożonych przez powierzchnię przebicia) i stosunek nośności z uwzględnieniem zbrojenia do sprowadzonej siły działającej. Zakres strefy zbrojenia dodatkowo jest prezentowany na rysunkach. W tabeli przedstawiono następujące parametry.

L1, L2 — zasięg zbrojenia od środka słupa w dwóch kierunkach prostopadłych

u — długość obwodu strefy zbrojenia wg zaleceń normowych

A — całkowita powierzchnia zbrojenia, jaką trzeba rozmieścić równomiernie wokół słupa w strefie zbrojenia określonej przez wysięg L1 i L2

n x ϕ — liczba i średnica prętów wyliczona na podstawie całkowitej powierzchni i ustawień w opcjach na przebicie.

Uwaga:

Dla normy Eurocode EN 1992-1-1 punkt 6.4.3 możliwe są trzy stany.

• Gdy v_Ed < v_Rd,c, zbrojenie na przebicie/ścinanie nie jest konieczne do przeniesienia sił działających.
• Gdy v_Ed > v_Rd,c i v_Ed < v_Rd,max, zbrojenie na przebicie/ścinanie jest konieczne.
• W ostatnim przypadku, w którym v_Ed > v_Rd,max, nośność na ścinanie jest niewystarczająca do przeniesienia sił działających.

Obliczenia oparte na punkcie 6.4.3(3) uwzględniają mimośród siły. Wartości Q i Q_adm są prezentowane w tabeli w oknie dialogowym, a opis przedstawia wartości obliczeniowe sił działających i wytrzymałościowych wraz z efektem mimośrodu. Mimośród jest uwzględniany na podstawie współczynnika zdefiniowanego przez Eurocode jako współczynnik β w równaniu (6.39). RSA w każdym przypadku uwzględnia mimośród dwuosiowy. Z tego powodu równanie (6.39) jest rozszerzane i ma dwie niezależne części dla M_x/W_1x i M_y/W_1y. Wartość Q_adm zależy od stanu projektu i reprezentuje dopuszczalną wartość na podstawie v_Rd,c, v_Rd,s lub v_Rd,max.

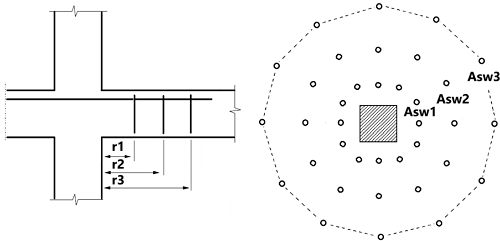
Gdy v_Ed > v_Rd,c i v_Ed < v_Rd,max, zbrojenie na ścinanie A_sw jest obliczane na podstawie równania (6.52). Obliczany jest również najbardziej zewnętrzny obwód zbrojenia na ścinanie u_out na podstawie wymagań normy Eurocode. Zakłada się, że maksymalny rozstaw łączników ścinania w kierunku stycznym s_t jest równy 2*d. Dla każdego obwodu zbrojenie jest takie samo z wyjątkiem sytuacji, w których ważne jest równanie A _sw,min (6.11). W takim przypadku r, u i A _sw są prezentowane w tabeli w oknie dialogowym i w opisie.

r_i reprezentują promienie obwodów

u_i — wartości długości obwodów.

A_sw — zbrojenie na ścinanie na podstawie równania (6.52)

n x ϕ jak powyżej

Kolejne wartości ​​ r_i u_i A_sw reprezentują wartości zgodnie z poniższym rysunkiem:

Uwaga: Dla brytyjskiej normy BS można podać kilka stref zbrojenia w zależności od wymagań (strefy zbrojenia mogą zachodzić na siebie). W kolejnych strefach rozmieszczana jest tylko ta część wyliczonych prętów, która pozostaje po odjęciu od niej prętów należących też do strefy poprzedniej.