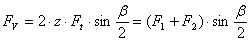Cálculo das proporções de resistência da correia trapezoidal

Equações gerais utilizadas


	Onde m é uma massa de correia específica definida como m = S ρ

Fator de atrito modificado da polia especificada


	f = f_g+ v f_mod

Equações fundamentais de polias impulsoras e correias

potência para transmitir

Velocidade de correia

Frequência de flexão da correia

Desmoldagem efetiva (ou tensão efetiva)

Força centrífuga

Fc = z m v 2

Tensão nos intervalos da correia

Com as equações seguintes, o aplicativo primeiro determina a polia com maior probabilidade de requerer a tensão máxima de instalação de correia para poder transmitir uma carga. Em seguida, a tensão da correia de cada intervalo é ajustada para todas as polias com respeito à tensão de instalação da correia inicial.


	F_1i- F_pP_xi- F_2i= 0

O critério para determinar a polia mais provável é a tensão do lado de máximo aperto

F 1máx = máx (F 1i)

A tensão máxima total no intervalo da correia (para cada correia) quando a transmissão da correia é localizada abaixo da carga completa é determinada como

Onde a expressão “k 1 F 1máx” é a tensão máxima real no espaço da correia considerado para todas as correias da transmissão. Deste modo, todas as tensões correspondentes dos diferentes segmentos são calculados novamente para cumprir a seguinte condição:

F 1i - F P P xi - F 2i = 0

Carga axial resultante para cada polia quando a transmissão da correia é localizada abaixo da carga completa

Observação: Nas polias motrizes e polias intermediárias, os valores F 1 e F 2 são invertidos no gerador, de modo que F 1 é a tensão na entrada do vão da correia e F 2 é a tensão na saída no sentido do movimento da correia.

Tensão de instalação inicial da correia e força de tensionamento estática

A tensão de instalação inicial da correia requerida (para cada correia) pode ser ajustada com o fator de tensão e é calculada do modo a seguir:

A força de tensionamento estático F v é determinada para cada polia. O aplicativo calcula a força de tensionamento que atua sobre o eixo dos intervalos da correia da forma seguinte:

Significado das variáveis utilizadas:

C	Força tangencial [N]
β	Arco de contato [graus]
α	Ângulo de setor [gr]
C	Força centrífuga [N]
N	Força normal [N]
m	Massa específica da correia [kg/m]
v	Velocidade da correia [m/s]
R	Raio de polia [m]
S	Área da seção transversal da correia [m²]
T	Torque em uma polia especificada [Nm]
D_p	Diâmetro do flanco de polia [m]
k	Número de polias [-]
P	potência para transmitir [N]
v	Velocidade da correia [m/s]
F_c	Força centrífuga [N]
F¹	Tensão no segmento da correia na entrada para a polia especificada [-]
F₂	Tensão no segmento da correia na saída para a polia especificada [-]
f	Fator de atrito alterado da polia especificada [-]
P_x	Taxa de potência da polia especificada [-]
f_g	Fator de atrito do material e correia da polia especificada [-]
f_mod	Fator de velocidade de modificação do atrito [s/m]
Z	Número de correias [-]
ρ	Densidade da correia [kg/m3]
F_t	Tensão inicial de instalação da correia [N
F_v	Força de tensionamento estática para a polia especificada [N]
k₁	Fator de tensão da correia [-]

Observação: i - índice da polia