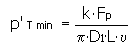Eixo oco

Eixo sólido

C 1 = C 1A + C 1B

Δ = p T D 1 C 1 + H

Interferência mínima praticável

A interferência mínima praticável é calculada a partir da condição da carga transmitida requerida. Uma interferência menor não transferiria a carga requerida.

	ou

Interferência máxima praticável

A interferência máxima praticável é calculada a partir da condição do limite de resistência do material. Uma interferência maior iria danificar o material do cubo ou do eixo.

Cubo	Eixo

Eixo oco

As seguintes desigualdades devem ser verdadeiras:

Δ' máx ≤ p' Amáx D 1 C 1 + H

Δ' máx ≤ p' Bmáx D 1 C 1 + H

Eixo sólido

As seguintes desigualdades devem ser verdadeiras:

Δ' máx ≤ p' Amáx D 1 C 1 + H

Δ' máx ≤σ B D 1 C 1 + H

A interferência mínima de ambas as desigualdades é selecionada como a interferência máxima.

Interferência máxima e mínima

O cálculo desenha um ajuste segundo as normas correspondentes (ISO, ANSI, JIS, etc.). O ajuste padrão não pode superar os limites máximo e mínimo da interferência. A interferência máxima e mínima pretendida para outra peça de cálculo é determinada a partir do ajuste selecionado. Se o ajuste correspondente não puder ser selecionado, os desvios serão expressos numericamente e serão calculados dividindo o campo de tolerância em duas metades.

Aumento do diâmetro externo da peça externa

Δ' máx ≤ p' Amáx D 1 C 1 + H

Δ' máx ≤σ B D 1 C 1 + H

A interferência mínima de ambas as desigualdades é selecionada como a interferência máxima.

Δ máx é substituído por Δ quando a redução máxima do diâmetro D2 tiver que ser calculada

Δ mín é substituído por Δ quando a redução máxima do diâmetro D2 tiver que ser calculada

Redução do diâmetro interno da peça interna

Δ máx é substituído por Δ quando a redução máxima do diâmetro D3 tiver que ser calculada

Δ mín é substituído por Δ quando a redução máxima do diâmetro D2 tiver que ser calculada

Cálculo da força de pressão

Cálculo da temperatura de aquecimento da peça externa

Cálculo da temperatura de aquecimento da peça interna

Torque

M p = Fp D 1 /2

Significado das variáveis utilizadas:

M p	Torque
E A	Módulo de elasticidade
E B	Módulo de elasticidade
μA	Coeficiente de Poisson
μB	Coeficiente de Poisson
D 1	Diâmetro externo da peça externa (cubo)
D 2	Diâmetro do ajuste a pressão (diâmetro nominal do ajuste calculado)
D 3	Diâmetro interno da peça interna (eixo)
L	Comprimento da conexão
F pmax	Força de pressão máx.
F pmin	Força de pressão mín.
k	Fator de segurança
ν	Fator de fixação
ν 1	Fator de fixação durante a pressão
σ A	Dilatação térmica da peça externa (cubo)
σ B	Dilatação térmica da peça interna (eixo)
H	Suavidade da superfície
V	Folga de montagem
P máx.	Pressão de contato máx.
P mín.	Pressão de contato mín.
p' Tmín	Pressão de contato mínima praticável
p Tmín	Pressão de contato mínima praticável
p Tmax	Pressão de contato máxima
p' Amáx	Pressão suportada no furo da peça externa
p' Bmax	Pressão suportada no furo da peça interna
Δ	Interferência
Δ' min	Interferência mínima praticável
Δ' máx.	Interferência máxima praticável
Δ min	Interferência mínima
Δ max	Interferência máxima
α A	Fator de dilatação térmica do material da peça externa
α B	Fator de dilatação térmica do material da peça interna
t	Temperatura básica