Podem ser utilizado diferentes tipos de curvas de fadiga para determinar a resistência à fadiga das juntas soldadas. A seguir, estão fórmulas para curvas individuais de tensão normal e de corte.

1. Método de tensão média virtual

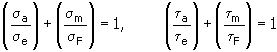
em que:

	σ a , τ a	amplitude de tensão normal (corte) [MPa, psi].
	σ e , τ e	limite de resistência com resistência constante [MPa, psi]
	σ m , τ m	tensão cíclica média [MPa, psi].
	σ F , τ F	tensão média virtual [MPa, psi]
	Ψ	fator de estreitamento do diagrama de Haigh [-]
		Depende do material da junta - valores recomendados - para tração e dobra Ψ<0,15...0,3>
		- para corte Ψ <0,1...0,25>.

2. Método Godman alterado

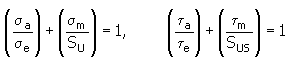
em que:

	σ a , τ a	amplitude de tensão normal (corte) [MPa, psi].
	σ e , τ e	limite de resistência com resistência constante [MPa, psi]
	σ m , τ m	tensão cíclica média [MPa, psi].
	S U	tensão máxima de tração [MPa, psi]
	S US	tensão máxima de corte [MPa, psi]
		enquanto S US ≈ 0,8 S U

3. Método quadrático (elíptico)

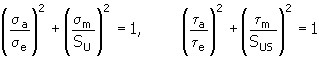
para obter explicações sobre as variáveis, consulte o tópico 2: método Godman alterado

4. Método Gerber parabólico

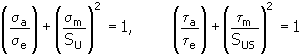
para obter explicações sobre as variáveis, consulte o tópico 2: método Godman alterado

5. Método de Keccecioglu, Chester e Dodge

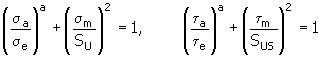
em que:

	σ a , τ a	amplitude de tensão normal (corte) [MPa, psi].
	σ e , τ e	limite de resistência com resistência constante [MPa, psi]
	σ m , τ m	tensão cíclica média [MPa, psi].
	S U	tensão máxima de tração [MPa, psi]
	S US	tensão máxima de corte [MPa, psi]
		enquanto S US ≈ 0,8 S U
	a	expoente dependente do material da junta [-]
		valores recomendados a <2,6...2,75>

6. Método de Bagci

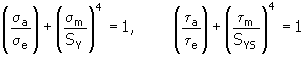
em que:

	σ a , τ a	amplitude de tensão normal (corte) [MPa, psi].
	σ e , τ e	limite de resistência com resistência constante [MPa, psi]
	σ m , τ m	tensão cíclica média [MPa, psi].
	S Y	resistência à tração de escoamento [MPa, psi]
	S YS	resistência ao corte de escoamento [MPa, psi]
		enquanto S YS ≈ 0,577 S Y

7. Método de Soderberg

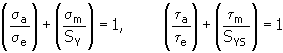
para obter explicação sobre as variáveis, consulte o item 6: método de Bagci