Designações adotadas:
E – módulo de Young
G – módulo de cisalhamento
ν – coeficiente de Poisson
fd – limite de elasticidade
Ax – área da seção transversal
Ix – constante de torção
Iy – momento de inércia – flexão no plano XZ
Iz – momento de inércia – flexão no plano YZ
ky, kz – coeficientes de correção da rigidez de cisalhamento nas direções Y e Z
L – comprimento da barra.
-
Observações preliminares e suposições
As seguintes suposições foram adotadas para os elementos de barra (viga):
- Formulação uniforme para 2D e 3D (estruturas 2D e 3D, grades)
- Elemento uniforme permitindo a não linearidade geométrica e/ou material
- Graus de liberdade de deslocamento padrão em 2 nós extremos
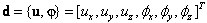
- É permitido o uso das seguintes operações:
- Deformação de cisalhamento incluída (modelo de Timoshenko).
- Seção transversal cônica – somente para não linearidade geométrica.
- Solo de Winkler.
- Há dois níveis de não linearidade geométrica disponíveis: P-Delta (teoria de segunda ordem) e Grandes deslocamentos, que é a teoria mais precisa possível com grandes deslocamentos e rotações; essa é uma abordagem incremental com uma atualização de geometria.
- Assumindo deslocamentos pequenos e ausência de não linearidade física para o limite, os resultados são idênticos aos dos elementos lineares padrão.
- Na análise de não linearidade do material, o modelo em camadas e o princípio de tensão-deformação constitutivo da tensão-deformação uniaxial no nível do ponto (camada) são aplicados.
- Os estados de cisalhamento e torção são tratados como linearmente elástico e precisam ser desacoplados das forças axiais e dos momentos de dobra no nível de seção transversal.
- As liberações e articulações não lineares podem ser definidas somente como elementos DSC.
- Todos os tipos de cargas de elementos são permitidos (da mesma forma que para elementos padrão). No entanto, presume-se que as forças nodais que atuam sobre uma estrutura são determinadas no início do processo. As alterações na transferência de cargas de elementos em nós resultantes de não linearidade geométrica ou material são ignoradas.
- Além do elemento elastoplástico, também é possível gerar articulações elastoplásticas em seções transversais de barra selecionadas como uma extensão da opção “articulações não lineares” (consulte o ponto 5).
-
Geometria, cinemática e aproximação de deformação
Geometria, convenção de sinais para forças, deslocamentos e tensões
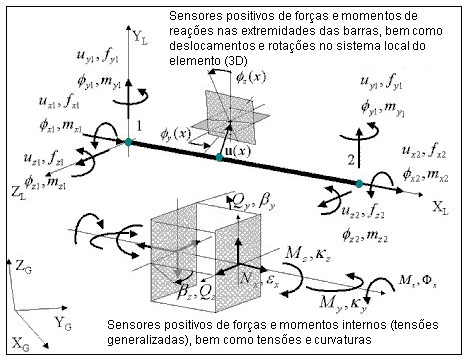
Relações cinemáticas básicas
No sistema local do elemento e na faixa geometricamente linear, as tensões generalizadas e no nível da seção transversal são as seguintes (o símbolo
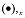indica o cálculo do diferencial ao longo da direção do eixo da barra):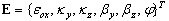 
em que:
Tensão axial no eixo da barra:
e0x = u ,x
Curvaturas:
K y = fy'x
K z = - f z'x
Ângulos médios (deformação):
b y = n 'x - f z'
b y = w 'x - f y
Ângulo de torção da unidade:
j = f x'x
Aproximação do deslocamento
Quando há a possibilidade de considerar a influência do cisalhamento e a consistência dos resultados obtidos para o elemento linear, as funções de forma física considerando a influência do cisalhamento foram implementadas.
Barras 2D:
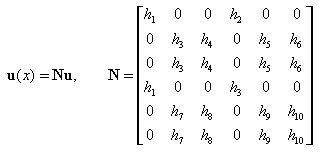
As funções de forma e seus derivados são expressos pelas fórmulas:
em que:
x = x / L
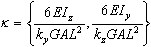para os planos XY e XZ, respectivamente. Relações cinemáticas para a notação da matriz (a teoria geometricamente linear)
Ao considerar a influência de tensões impostas
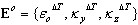
Incremento de tensões generalizadas (secionais):
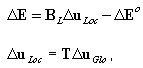
2D:
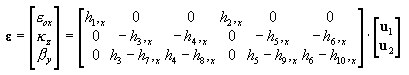
3D:
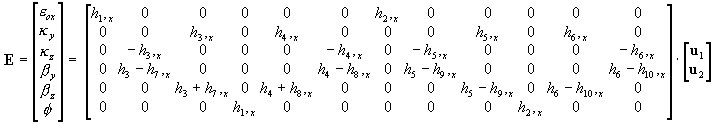
em que:
Esforços em um ponto (camada)
Dadas as tensões generalizadas {ε 0x, k y , k x } de uma seção transversal, a tensão exl ou seu incremento Dexl em qualquer ponto da seção transversal l – das coordenadas yl, zl, é calculado como
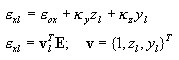
finalmente, o incremento de tensão na camada:
-
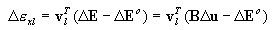
Tensões e forças internas dentro de um elemento
O princípio constitutivo no nível do ponto
O princípio é adotado na forma incremental geral, onde as tensões de corrente σ x n + 1 são definidas como uma função da tensão para o último equilíbrio σ x n e incremento de deformação atual com deformações (térmicas) impostas consideradas,
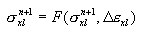
com base na função σ = f(ε) que descreve a relação no processo de carga ativa e na especificação do princípio de descarga e recarga. Em particular, pode ser o princípio elastoplástico com endurecimento linear e o princípio especificado de descarga, como (a) elástico, (b) plástico, (c) danos, (d) misturado. Para descarga elástica, o processo ativo e passivo é executado ao longo do mesmo caminho σ = f(ε). Para os restantes, é executada ao longo da linha reta determinada pelo ponto inicial de um determinado processo de descarga {ε UNL, σ UNL } e o módulo de descarga D UNL definido como
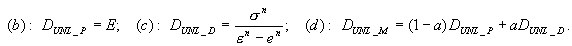
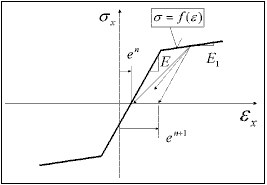
e n é uma deformação memorizada, para a qual o processo ativo atual foi iniciado, iniciada após exceder 0 por tensões com o descarregamento (e 1 = 0) assumido.
Para a análise, é necessário fornecer a rigidez atual presumida como derivativa
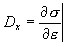
Cálculo de forças e valores de rigidez da seção transversal.
No nível de seção transversal, o vetor de forças internas (resultantes de tensão) é composto por:
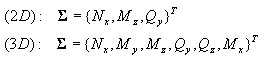
Os estados de cisalhamento e de torção ΣST são tratados como linearmente elásticos e não conjugados com o estado das forças axiais/de dobra no nível de seção transversal.
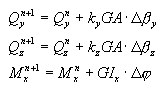
Os estados de compressão/tensão Σ NM são geralmente tratados como conjugados ao aplicar a abordagem em camadas. No entanto, desde que o estado elástico seja garantido, ou seja, até que as tensões generalizadas atuais atendam à seguinte condição de estado elástico:
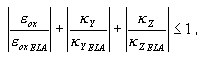
em que:
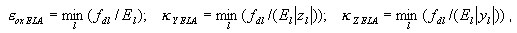
a seção transversal é tratada como elástica e a abordagem em camadas não é ativada.
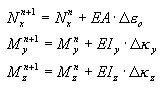
Uma vez que a violação da condição de estado elástico é confirmada, as tensões induzidas por tensões axiais e dobra são calculadas separadamente para cada camada e com base nas quantidades secionais
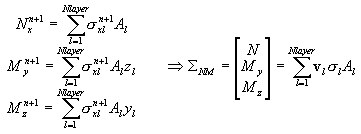
A rigidez no nível da seção transversal D é calculada como segue:
no estado elástico como:
D = diag {EA, EIy, EIz, KyGA, kzGA, GIx)
Após exceder a condição de estado elástico como:
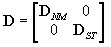
em que:
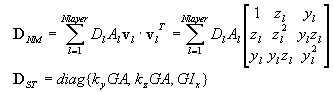
Matriz de rigidez de elemento e vetor de força nodal
Eles são calculados por meio das fórmulas padrão que aplicam a quadratura de Gauss (Ngauss=3).
-
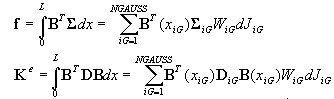
Não linearidade geométrica
As seguintes configurações são levadas em consideração:
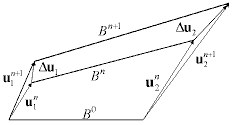
B0 – configuração inicial
Bn – configuração de referência (a última para a qual as condições de equilíbrio são satisfeitas)
Bn+1 – configuração atual (iterada)
Um ponto de entrada para a formulação do elemento é o princípio de trabalho virtual salvo na seguinte forma para incrementos de deslocamento:
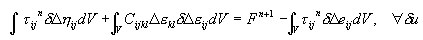
em que: Δε incremento de deformação enquanto move Bn para Bn + 1, Δe, Δη constituem suas partes, correspondentemente: linear e não linear em relação ao incremento de deslocamento Δu, enquanto τ é uma tensão referente à configuração de referência e Cijkl é um tensor de módulos de elasticidade tangencial.
Opção Não linearidade
Corresponde à formulação não linear ou a teoria da segunda ordem. Como a não linearidade do material é possível, a formulação incremental está sendo introduzida (no entanto, sem modificação da geometria do elemento).
Relações cinemáticas
Incrementos de tensão na notação da matriz:
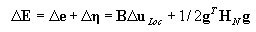
em que:
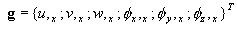
então, o gradiente de incremento de deslocamento g = ΓΔu
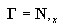
enquanto
é uma matriz de seleção.
Matriz de rigidez de elemento e vetor de força nodal
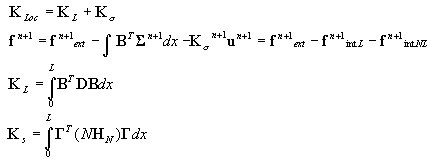
Algoritmo no nível do elemento
A geometria do elemento não é modificada; a transformação local-global é executada com o uso da matriz de transformação inicial 0 T
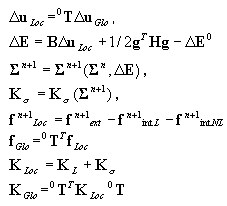
Opção de deslocamento grande
É uma certa variante da descrição da barra que permite grandes deslocamentos. A abordagem da descrição do Lagrange atualizada é aplicada aqui.
Matriz de rigidez de elemento e vetor de força nodal
-
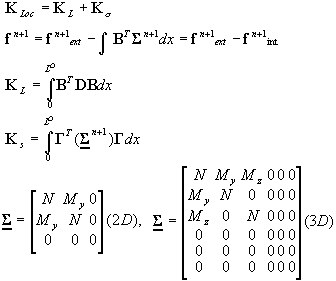
Articulações elastoplásticas
Como alternativa, é possível modelar o trabalho elastoplástico de uma estrutura ao introduzir articulações não lineares em seções transversais de barra selecionadas. As características de uma articulação representada por um elemento DSC de 2 nós são definidas aplicando o algoritmo de análise de seção transversal descrito no ponto 3, presumindo que a função das tensões generalizadas E é executada por deslocamentos de nós mútuos (com relação às direções locais da barra) divididos pelo comprimento do elemento adotado (fictício) (ΔL) que é igual à altura mínima da seção transversal. Elas atuam como o volume do elemento dV=ΔL. As forças e os deslocamentos de nós recém-gerados do elemento DSC constituem graus de liberdade globais, ou seja, não sofrem condensação.
Algoritmo no nível do elemento-
cálculo de tensões generalizadas em uma seção transversal
-
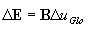
cálculo de forças internas (resultantes de tensão) e rigidez da seção transversal de acordo com o ponto 3.2
-
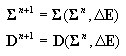
cálculo de forças (reações nas extremidades da barra) e rigidez do elemento DSC
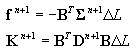
em que:
-
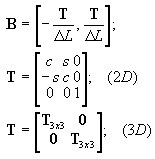