Durante os cálculos de uma laje ortotrópica, uma rigidez equivalente em um nível de seção é calculada em cada ponto. Para um elemento de casca 2D em 3D, a rigidez é determinada com base nas seguintes matrizes:
- Matriz de rigidez de membrana D.
- Matriz de rigidez de flexão K.
- Matriz de rigidez de cisalhamento H.
Considerando que a ortotropia seja definida somente para elementos 2D e que a seção seja simétrica, não será necessário determinar as matrizes que combinam os estados de flexão e de membrana.
As seções de nervuras unidirecionais de dois lados, pisos de caixas unidirecionais, pisos de caixas bidirecionais e grelhas constituem seções simétricas, e a abordagem indicada acima é totalmente justificada. No entanto, para os tipos restantes, a abordagem indicada acima produz somente uma aproximação.
O plano de referência para definir a rigidez deve ser adotado no nível do centro de gravidade, em vez de uma linha média (espessura da placa). Trata-se de uma abordagem mais correta, levando em conta especialmente as vibrações transversais. No entanto, também constitui uma aproximação ao calcular a rigidez, mas é melhor do que adotar a espessura como uma linha média.
A rigidez da laje é determinada com base nas seguintes matrizes:
- Matriz de rigidez de flexão K.
- Matriz de rigidez de cisalhamento H.
Os valores de rigidez que se referem às direções de ortotropia são fornecidos pelas matrizes considerando-se a forma geral:
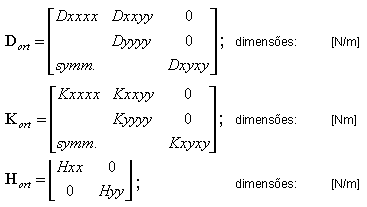
A direção de ortotropia X é definida pelo usuário (uma definição de vetor de direção) da mesma forma que quando é definido o sistema local para a apresentação de resultados ou da armadura V =[vx,vy,vz].
A regra usada para determinar como o vetor V definido pelo usuário gera a direção do eixo X do sistema de ortotropia:
“A direção X é a direção tangencial ao plano do elemento que está mais próximo da direção V definida”.
Se {e 1 ;e 2 ;e 3 } constituir uma base local no ponto de determinado elemento (para placas em 2D, e i coincide com as direções dos eixos globais XG, YG), as funções trigonométricas sin α; cos α de um ângulo incluído entre a direção de ortotropia X e o eixo local x1 serão definidas como:
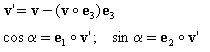
Após as funções trigonométricas s = sin α; c = cos α de um ângulo serem determinadas, as matrizes de rigidez serão transformadas do sistema do eixo de ortotropia XY para as direções locais em um elemento, aproveitando as seguintes fórmulas:
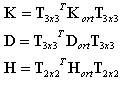
em que:
T3x3 é a matriz de transformação para o tensor de segunda ordem em 2D (apresentada como a matriz 3x3)
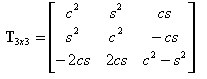
T2x2 é a matriz que apresenta a transformação do vetor 2D
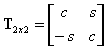
Consulte também: