Cálculo de área crítica e circunferência crítica
A forma da área crítica depende da geometria de suporte ou do cabeçote de suporte, do ângulo de inclinação da superfície sujeita a corte, bem como da posição em relação às arestas e cantos da laje. A forma e o tamanho da área crítica são determinados estritamente na norma, mas para cada cálculo de norma consiste em determinar a área sujeita à ação de uma força de punção. No cálculo disso, as arestas de zona da laje e das aberturas são consideradas. A tabela exibe o comprimento da circunferência crítica “u”. Observe que o efeito das aberturas no comprimento da circunferência crítica é considerado no programa.
A = u * d
em que:
A – Área crítica
u – Comprimento da circunferência crítica
d – Altura utilizável da seção da laje.
Cálculo de forças de punção limite ou tensões limite
Essa etapa de cálculos inclui determinar os valores máximos de força de pressão permitidos pela norma ou de tensões máximas que podem ser carregadas por uma seção de concreto. A força limite (máxima) é o resultado da área crítica e das tensões permitidas pela norma.
Qadm = τ * A
em que:
Qadm – Força de punção admissível
τ – Tensão admissível
A – Área crítica.
Cálculo de forças de punção ou tensões resultantes de impacto externo
Cada uma das normas determina a forma como uma força ou tensão causada por impacto externo deve ser recebida na área de punção. No caso mais simples, os cálculos envolvem a multiplicação de uma força de punção por um fator apropriado, enquanto nos mais complicados, os cálculos de tensões considerando os momentos atuantes são necessários. A tabela exibe um valor da força de projeto do cálculo Q, obtido com base na fórmula.
Q = τ * A
τ = V / A
![]() (para a norma ACI)
(para a norma ACI)
em que:
Q – Força de projeto de cálculo
τ – Tensão na área crítica
V – Força de punção máxima
Mx, My, V – Momentos de dobra e a força no centro de gravidade da área crítica
Jx, Jy – Momentos de inércia da área crítica com relação aos eixos que passam através de seu centro de gravidade
γ x , γ y, c x , c y – Parâmetros dependendo da geometria da área crítica [ACI 318 11.12.2.2].
Para o Eurocódigo EN 1992-1-1, com base no ponto 6.4.3(3), os cálculos incluem a excentricidade da força. A excentricidade é levada em conta com base em um fator definido pelo Eurocódigo como coeficiente β na equação (6.39). A análise do espectro de resposta em cada momento inclui a excentricidade biaxial. Por causa disso, a equação (6.39) é estendida e tem duas partes independentes para Mx/W1x e My/W1y.
Verificação da condição de capacidade de carga
Isso consiste em comparar tensões ou forças causadas por impacto externo com valores limite. Há três estados possíveis.
- Se as tensões calculadas forem menores que as admissíveis para uma seção de concreto, a armadura não será necessária.
- Se as tensões forem maiores que as admissíveis para uma seção de concreto e simultaneamente menores que as admissíveis, a armadura será necessária.
- Se as tensões forem maiores que as tensões admissíveis, a seção da laje será muito pequena.
Quando a armadura não é necessária ou quando uma seção da laje é muito pequena, os resultados são apresentados em uma forma da força de punção máxima (para cálculos com base em tensões, a força é calculada com base nas tensões multiplicadas pela área de punção) e a relação de força admissível com força de ação equivalente. Se a armadura for necessária, os cálculos da armadura necessária serão executados pelo programa.
Cálculo da armadura necessária
Se as tensões forem maiores que as admissíveis para uma seção de concreto e simultaneamente menores que as admissíveis, a armadura de punção calculada será necessária. Os cálculos são executados de acordo com as diretrizes da norma relativas à armadura da barra. A área de armadura necessária e a faixa de uma zona na qual a armadura é necessária são mostradas na tabela na guia Punção. Também estão disponíveis a força de puncionamento (para cálculos com base em tensões, a força é calculada com base nas tensões multiplicadas pela área de puncionamento) e a relação da capacidade de carga com armadura considerada para a força atuante equivalente. A faixa de zona de armadura é também apresentada nos desenhos. A tabela mostra os seguintes parâmetros.
L1, L2 – A armadura varia do centro do membro em ambas as direções perpendiculares.
u – Comprimento da circunferência da zona de armadura de acordo com as recomendações da norma.
A – Área total da armadura que deve ser distribuída uniformemente em torno da coluna dentro da zona de armadura determinada pelos comprimentos L1 e L2.
n x ϕ – Número e diâmetro de barras calculado com base na área total e configurações nas opções de punção.
Para o Eurocódigo EN 1992-1-1, ponto 6.4.3, são possíveis três estados.
- Quando vEd < vRd,c, a armadura de cisalhamento de punção não é necessária para manter as forças atuantes.
- Quando vEd > vRd,c e vEd < vRd,max, a armadura de cisalhamento de punção é necessária.
- No último caso, em que vEd > vRd,max, a resistência ao cisalhamento é insuficiente para manter as forças atuantes.
Com base no ponto 6.4.3(3), os cálculos incluem a excentricidade da força. Os valores Q e Qadm são apresentados na tabela da caixa de diálogo. A nota representa os valores do projeto das forças atuantes e de resistência, incluindo os efeitos de excentricidade. A excentricidade é levada em conta com base em um fator definido pelo Eurocódigo como coeficiente β na equação (6.39). A análise do espectro de resposta em cada momento inclui a excentricidade biaxial. Por causa disso, a equação (6.39) é estendida e tem duas partes independentes para Mx/W1x e My/W1y. Qadm depende do estado do projeto e representa o valor admissível com base em vRd,c, vRd,s ou vRd,max.
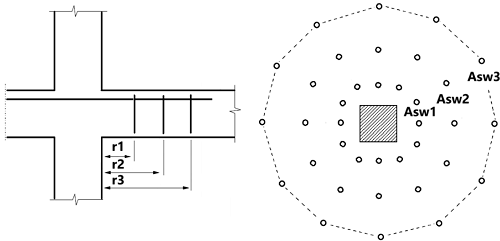
Quando vEd > vRd,c e vEd < vRd,max, a armadura de cisalhamento Asw é calculada com base na equação (6.52). O perímetro mais externo da armadura de cisalhamento uout com base nos requisitos do Eurocódigo também é calculado. A suposição é que o espaçamento máximo dos vínculos de cisalhamento na direção tangencial st é igual a 2*d. Para cada perímetro, a armadura é a mesma, exceto nas situações em que a equação A sw,min (6.11) é importante. Nesse caso, r, u e A sw são apresentados na tabela da caixa de diálogo e na nota.
ri representam os raios dos perímetros
ui – os valores dos comprimentos dos perímetros.
Asw – armadura de cisalhamento com base na equação (6.52)
n x φ como acima