Cálculo da qualidade de triângulos (elementos de malha)
Quando uma malha triangular é gerada, você deve definir a malha de forma que seus elementos gerados sejam triângulos equiláteros. Outros triângulos, especialmente triângulos obtusângulos, são elementos de malha “piores” de um ponto de vista do Método de elementos finitos (FEM).
Assumindo que um coeficiente de qualidade dos elementos de malha triangulares esteja no intervalo de <0,1>, aceitamos o coeficiente α igual a 1 para um triângulo equilátero.
Calcule o coeficiente α para um triângulo com os índices ABC com base na seguinte fórmula:
Esse algoritmo é baseado no cálculo de um produto vetorial de dois vetores no espaço.
Cálculo da qualidade de quadriláteros (elementos de malha)
O quadrilátero ideal para criar uma malha quadrilateral é um retângulo. Um método de cálculo de coeficientes de triângulo é usado para calcular o coeficiente α.
Qualquer ABCD quadrilateral é dividido em quatro triângulos sobrepostos (ABC, ACD, ABD e BCD). O cálculo dos coeficientes α é feito para triângulos particulares: { α1, a2, α3, α4} = { α (ABC), α (ACD), α (ABD), α (BCD)}. Quando esses coeficientes são calculados, um coeficiente de qualidade quadrangular é calculado.
temp1 = α1 * α3;
temp2 = α2 * α4;
if( temp1 * temp2 != 0 )
α= ( temp1 > temp2 ) ? temp2 / temp1 : temp1 / temp2;
α_rect = 0.86602540000000;
α_avg = (α_rect – fabs((α1 + α2 + α3 + α4) / 4. - α_rect))/ α_rect;
if (α_avg < α) α= α_avg;
Cálculo de um coeficiente de qualidade de malha global
Há duas maneiras de calcular um coeficiente global:
- Os valores de qualidade de todos os elementos de malha (triângulos, quadriláteros) são calculados.
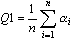
em que n – número do elemento de malha
- É calculada a média dos valores de qualidade ponderados de todos os elementos de malha (triângulos, quadriláteros), nos quais o peso é uma área de elemento de malha.
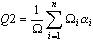
em que n – número do elemento de malha, Ω – área