Introdução
Este documento apresenta a descrição dos métodos de análise dinâmica aplicados no Robot. Os pormenores teóricos e os exemplos estão incluídos nos anexos. Esta seção não é instrutiva e não tem como objetivo detalhar a interface do Robot. Expõe as principais ideias desenvolvidas neste programa.
A maioria dos métodos dinâmicos no Robot está baseada nos resultados da análise modal. É necessário entender que os métodos de análise modal dependem de um tipo de solver selecionado. Para o solver de linha do horizonte, os seguintes métodos estão disponíveis: iteração de subespaço do bloco (BLSI), iteração de subespaço (SI), Lanczos e redução de base. Os métodos disponíveis para o solver direto esparso são os seguintes: iteração de subespaço do bloco (BLSI), Lanczos e redução de base. Já no caso do solver iterativo, os seguintes métodos estão disponíveis: Lanczos modificado (pseudomodo – consulte o ponto 3.5 e os anexos 3A e 3B), gradiente Ritz (PCG_Ritz) e gradiente conjugado pré-condicionado (PCG).
O solver direto esparso (SPDS) é uma forma específica de eliminação de Gauss. É altamente recomendado para a análise de problemas de média e larga escala (10.000 – 200.000 equações) e uma boa alternativa para o solver iterativo.
3.1. Métodos de análise modal
A análise modal é composta por duas abordagens básicas. A análise de problemas de valor próprio
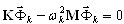 k = 1,2,...,N (3.1)
k = 1,2,...,N (3.1)
é produzida pela definição dos valores próprios wk e dos vetores próprios 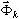 . É a primeira abordagem familiar aos engenheiros. A segunda abordagem consiste na geração de vetores de base
. É a primeira abordagem familiar aos engenheiros. A segunda abordagem consiste na geração de vetores de base
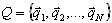 (3.2)
(3.2)
e na pesquisa das aproximações de Ritz![]() ,
, ![]() (k=1,2,...,N). Baseia-se no método de vetores Ritz dependentes de carga, proposto por E.L. Wilson [1, 3] e aplicado no SAP2000. Essa abordagem é aplicada para análise sísmica e é um método muito eficaz quando existem grandes dificuldades em obter uma porcentagem de massa suficiente (consulte a seção 3.5).
(k=1,2,...,N). Baseia-se no método de vetores Ritz dependentes de carga, proposto por E.L. Wilson [1, 3] e aplicado no SAP2000. Essa abordagem é aplicada para análise sísmica e é um método muito eficaz quando existem grandes dificuldades em obter uma porcentagem de massa suficiente (consulte a seção 3.5).
Os métodos de iteração de subespaço do bloco (BLSI), iteração de subespaço (SI), Lanczos de ortogonalização seletiva e redução de base (consulte o anexo 3A) são usados quando os solvers diretos (linha do horizonte ou SPDS) estão selecionados. Normalmente, o método de iteração de subespaço é lento. Portanto, a aplicação dos métodos BLSI ou Lanczos é altamente recomendada para a análise de problemas de média e, especialmente, de larga escala, quando é necessário um grande número de pares próprios. O método de redução de base pode ser muito eficaz para um engenheiro experiente; no entanto, esse método exige informações adicionais sobre os nós de base e as direções de base apropriadas.
Gradiente conjugado pré-condicionado (PCG)
Esse método é usado na primeira abordagem, quando um solver iterativo está selecionado. Essa abordagem pode ser muito eficiente quando é extraído um número pequeno de modos próprios (no máximo 5). Deve ser usada para a análise de vento, e não para análise sísmica. O método PCG pode ser usado para a estimativa do modo próprio de nível mais baixo quando é identificado um problema de larga escala.
A segunda abordagem (realizada pela análise de pseudomodo) é apresentada na seção 3.5.
Iteração de subespaço do bloco (BLSI)
Esse método [1,3] é mais geral do que o Lanczos, pois permite a implementação de todos os tipos de matrizes de massa (consulte a seção 3.2) e é capaz de analisar estruturas separadas. Normalmente, as iterações em um bloco de tamanho constante com exclusão imediata de vetores convergidos e adição de novos vetores iniciais garantem cálculos mais rápidos em comparação com o método de iteração de subespaço normal [1-3]. Assim como o Lanczos, o método BLSI pode ser aplicado para extrair um grande número de pares próprios (até 100 – 200).
Iteração de subespaço (SI)
É possível usar esse método para a análise de todos os tipos de matriz de massa [4] e para a análise de estruturas separadas. No entanto, caso seja necessário um grande número de modos (aproximadamente N > 10), esse método ainda é muito demorado, especialmente para problemas de larga escala.
O método Lanczos [12,16,17] é um método muito eficaz que permite obter um grande número de pares próprios (N ~ 20 – 500 e mais). Embora seja preferível para problemas de larga escala, tem as seguintes limitações:
- Não é possível analisar estruturas separadas
- O tipo de matriz de massa deve ser fragmentado com rotações ou ser consistente
- Não é possível ignorar a densidade do material (nesse caso, basta atribuir uma densidade pequena fictícia para evitar essas limitações).
Redução de base
Este método [5] é conhecido como o método aprimorado Rayleigh-Ritz [4] ou método Bubnov-Galerkin para sistemas discretos. Esse algoritmo permitirá obter valores aproximados dos primeiros pares próprios se algumas informações sobre eles forem conhecidas. Esse método requer a atribuição de um grau de liberdade principal (MDOF) para obter o sistema reduzido. Dessa forma, é possível controlar o processo de criação do modelo reduzido. Essa é uma ferramenta muito eficaz para quem tem experiência na análise dinâmica de estruturas e lida com o mesmo tipo de estruturas, cujo comportamento é conhecido. Esse método permite a exclusão de graus de liberdade (DOF) indesejados do modelo reduzido e reduz o problema complexo inicial com um grande número de DOFs para uma forma reduzida. Isso é obtido com um número consideravelmente menor de graus de liberdade. A experiência com a análise dinâmica de estruturas demonstra que o usuário pode enfrentar alguns problemas quando os métodos de redução automática (BLSI, SI e Lanczos são levados em conta) geram um processo de cálculo muito complexo. Por exemplo, os modos de vibração local de barras únicas podem provocar problemas sérios, já que o processo de cálculo procura os pares próprios automaticamente sem nenhuma seleção. Isso deve ser observado na maioria dos casos de estruturas reais. Caso contrário, essas vibrações locais serão limitadas por algumas restrições não levadas em conta no modelo FEM, ou sua contribuição não será essencial para o movimento geral do sistema. Normalmente, a porcentagem de massa é muito pequena para essas vibrações locais. Neste caso, o uso de métodos exatos provoca as dificuldades mencionadas. No entanto, a implementação do método aproximado de redução de base pode simplificar consideravelmente o processo de cálculo.
Gradiente conjugado pré-condicionado (PCG)
Esse método [9-13] está disponível para os solvers iterativos. A aplicação de tal método é recomendada para extrair um pequeno número de pares próprios quando é identificado um problema de larga escala. A implementação do pseudomodo (consulte o ponto 3.5) com os métodos Lanczos modificado ou PCG_Ritz será recomendada se for necessário determinar um grande número de modos ao executar a análise sísmica ou espectral e um solver iterativo estiver selecionado.
Gradiente Ritz (PCG_Ritz)
Esse método [8] está disponível para os solvers iterativos no pseudomodo. Ele permite produzir uma solução aproximada em termos de vetores Ritz. É um método muito rápido para a análise sísmica e espectral de média dimensão (10.000 – 100.000 equações).
Lanczos modificado
Esse método é uma extensão do método Lanczos quando um solver iterativo é aplicado. Ele funciona como o método Lanczos no pseudomodo. No entanto, por ser diferente do método Lanczos para os solvers diretos, pois não exige a fatoração de uma matriz de rigidez. Em vez disso, são implementados princípios do método de gradiente pré-condicionado. Tal abordagem é a mais robusta entre todos os métodos dinâmicos dos solvers iterativos, embora normalmente não pareça ser a mais rápida.
As informações de todos os métodos dinâmicos são apresentadas no anexo 3A.
3.2. Tipos de matriz de massa
É possível aplicar as matrizes de massa de análise dinâmica de tipo fragmentado sem rotações, fragmentado com rotações e consistente a uma estrutura.
Os tipos fragmentado sem rotações e fragmentado com rotações são as matrizes de massa diagonal. Esses tipos de matrizes de massa exigem um esforço de cálculo mínimo.
A matriz de massa consistente aparece quando é considerado um sistema com parâmetros distribuídos. Normalmente se entende que uma matriz de massa consistente descreve as propriedades inerciais de uma estrutura mais exatamente do que uma matriz de massa fragmentada. No entanto, na maioria dos casos, uma matriz de massa fragmentada fornece uma boa aproximação, já que é óbvio que os parâmetros inerciais podem ser apresentados com menos precisão do que os parâmetros de rigidez. Na verdade, a energia cinética é descrita como deslocamentos de uma estrutura, mas a energia potencial é expressa através da derivada espacial dos deslocamentos. É um fato conhecido que o erro de aproximação aumenta consideravelmente durante cada diferenciação [4]. Portanto, para objetos contínuos (sólidos, cascas, placas), é possível aproximar para a mesma malha os parâmetros de massa de forma menos precisa do que os parâmetros de rigidez.
Normalmente, os polinômios Hermite são usados como funções de forma para barras. Isso oferece uma solução exata para a maioria dos problemas estáticos e dinâmicos quando é considerada uma matriz de massa fragmentada. No entanto, as soluções exatas para problemas dinâmicos de uma barra com massas distribuídas pertencem à classe das funções Krylov (uma combinação específica de funções hiperbólicas e trigonométricas). Isso permite que os parâmetros de rigidez sejam apresentados de forma aproximada quando os polinômios de Hermite são usados simultaneamente com uma matriz de massa consistente. Isso não se destina à implementação de um tipo diferente de função de forma para problemas estáticos e dinâmicos. Portanto, na maioria dos casos, não é um grande benefício complicar o modelo dinâmico usando parâmetros de massa distribuída, já que ocorre a solução aproximada com massas consistentes em vez da solução exata para um modelo aproximado (massas fragmentadas).
Além disso, normalmente as massas de elementos estruturais de barra (longarinas, colunas etc.) são insignificantes em comparação com as massas de paredes e telhados (carga morta), que são levadas em conta através da conversão de cargas mortas em massas. Essas massas não estruturais normalmente reduzem os efeitos das massas de elementos distribuídos.
Na maioria dos casos práticos, a matriz de massa fragmentada garante uma aproximação suficientemente precisa das propriedades inerciais da estrutura. É importante lembrar que uma matriz de massa consistente exige esforços de cálculo consideráveis quando é analisado um problema de larga escala. A implementação de uma matriz de massa consistente deve ser justificada antes da seleção desse tipo de matriz para análise.
Considera-se que a matriz de massa deverá ser consistente se os vínculos rígidos forem usados no modelo de cálculo.
Se um solver direto esparso ou um solver iterativo for aplicado, a técnica de elemento por elemento (EBE) será usada para o cálculo do produto de matriz-vetor. A matriz de massa consistente nunca pode ser montada; no entanto, todas as operações são executadas somente no âmbito do elemento. Para o solver de horizonte, uma matriz de massa consistente é montada e armazenada da mesma forma que uma matriz de rigidez. Para problemas de pequena escala (aproximadamente 3.000 equações, no máximo), a técnica de horizonte é mais rápida, embora ainda seja extremamente demorada quando o tamanho de um problema aumenta.
É possível usar massas adicionadas e converter cargas estáticas em massas.
Quando os métodos Lanczos, PCG_Ritz ou Lanczos modificado (solver iterativo) estão selecionados, somente estão disponíveis as matrizes de massa de tipo fragmentado com rotação e consistente.
3.3. Limites superiores
É possível calcular todos os valores próprios e os modos próprios que não ultrapassem um valor definido pelo usuário. Esse valor é tratado como o “limite superior”. Quando ativado, o Robot pesquisa ω1, ω2, …, ωn ≤ ω*, em que ω* é o limite superior. O algoritmo funciona em duas etapas. A verificação da sequência Sturm é executada na primeira etapa, definindo o número de “n” valores próprios que são menores do que o limite superior. Na próxima etapa, o algoritmo gera “n” pares próprios, cada um menor do que o limite superior.
Os métodos Lanczos e BLSI são recomendados para o tipo de análise que usa limites superiores, já que é necessário obter um grande número de pares próprios.
O critério de porcentagem de participação de massa (consulte a seção 3.4) é ignorado quando o limite superior está ativado.
Por exemplo, podem surgir problemas ao usar a norma sísmica francesa PS-92, porque é necessário que todas as frequências menores que 33 Hz sejam levadas em consideração.
3.4. Porcentagem de participação de massa
A porcentagem de massa para cada modo (k=1,2,...,N) é definida como
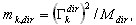
em que 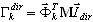 ,
, 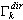 é o fator de participação de massa do modo próprio k, Idir é o vetor de conversão de unidade na direção (dir = X,Y,Z),
é o fator de participação de massa do modo próprio k, Idir é o vetor de conversão de unidade na direção (dir = X,Y,Z), 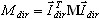 é a massa total na direção dir,
é a massa total na direção dir, 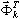 é o modo próprio k-th,
é o modo próprio k-th, 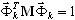 .
.
A porcentagem de massa da direção dir é igual a M%dir  . Isso define a contribuição de todos os modos envolvidos no movimento de uma estrutura na direção considerada.
. Isso define a contribuição de todos os modos envolvidos no movimento de uma estrutura na direção considerada.
Se a análise modal estiver selecionada e a porcentagem de massa para um número máximo de nós especificado for menor do que o necessário, um prompt avisará sobre a porcentagem de massa insatisfatória enquanto os cálculos continuarem sem correções.
É necessário definir a análise sísmica ou de pseudomodo para garantir a pesquisa automática da porcentagem de massa exigida. Os detalhes são apresentados na seção 3.5.
3.5. Modos de análise
Os modos de análise modal, sísmico e pseudodinâmico (regimes) são apresentados nesta seção.
Várias normas sísmicas (UBC-97, norma francesa PS-92) exigem que a soma das massas de cada direção (ou somente de direções horizontais) não seja inferior a 90%. Podem surgir problemas ao obter a soma exigida de massas devido a contribuições de pequena dimensão de muitos dos modos de nível mais baixo. Normalmente, isso é causado pelo caráter local dos modos de nível mais baixo. O modos sísmico e o pseudomodo são apresentados para melhorar a situação de problemas tão difíceis. A eficácia de tais abordagens é ilustrada no anexo 3C. O método Lanczos para os solvers diretos está disponível para esses dois modos. Quando o solver iterativo está selecionado, os métodos Lanczos modificado e PCG_Ritz estão disponíveis para o pseudomodo.
Modal
Esse modo constitui uma abordagem bem conhecida implementada nas versões anteriores do Robot.
Estão disponíveis os métodos BLSI, SI, Lanczos e de redução de base para os solvers diretos e o método PCG para o solver iterativo.
Os critérios de convergência para os solvers diretos são os seguintes. As iterações param quando  , em que i = 1, 2, ..., N; k – é o número de iteração, N – número de modos (definido pelo usuário). O método de redução de base não produz a verificação de convergência, já que não se trata da abordagem iterativa, embora seja uma espécie de método Ritz. O número de DOFs principais precisa ser aumentado para melhorar a precisão do resultado.
, em que i = 1, 2, ..., N; k – é o número de iteração, N – número de modos (definido pelo usuário). O método de redução de base não produz a verificação de convergência, já que não se trata da abordagem iterativa, embora seja uma espécie de método Ritz. O número de DOFs principais precisa ser aumentado para melhorar a precisão do resultado.
Os critérios de convergência para o método PCG (solver iterativo) incluem o seguinte:
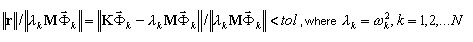
Os detalhes estão descritos no anexo 3A.
Os limites superiores correspondem ao valor de limite inferior para o período, frequência e pulsação. Se esse parâmetro for diferente de 0, serão calculados todos os pares próprios sequenciais de 0 até o limite superior.
O percentual de massa é a porcentagem de massa (soma das massas de todos os modos calculados para cada direção).
A verificação de Sturm é uma verificação de pares próprios ignorados entre 0 e o parâmetro de deslocamento ![]() e consiste em contar os elementos negativos na diagonal da matriz deslocada decomposta
e consiste em contar os elementos negativos na diagonal da matriz deslocada decomposta 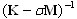
Trata-se de um procedimento muito caro para problemas de larga escala. Vale destacar que, para a análise sísmica e espectral, não é necessário obter os espectros contínuos dos valores próprios. É importante apenas garantir a porcentagem de massa modal suficiente para cada direção. Se tal condição for satisfeita, a integridade da base estará assegurada. A implementação do método BLSI permite produzir a verificação parcial de continuidade de espectros de valores próprios sem executar a verificação de Sturm. Consulte a descrição do método BLSI para obter mais informações.
|
Número de modos |
Limites superiores |
Percentual de massa |
Comportamento do programa |
|---|---|---|---|
|
N |
0 (inativo) |
0 (inativo) |
A verificação de Sturm está marcada. As frequências ignoradas para os N primeiros modos estão ausentes. Está disponível para os solvers diretos quando são aplicados os métodos BLSI, SI ou Lanczos. Não está disponível para o método de redução de base e todos os métodos de solver iterativo. São definidos os N primeiros modos próprios sequenciais. A verificação de Sturm é executada. Se as frequências ignoradas forem detectadas, um aviso solicitará o número das frequências ignoradas. Se indicado Sim, o processo de iteração continuará enquanto o número de pares próprios ignorados é determinado. Depois, repete-se a verificação de Sturm. Não, os pares próprios convergidos serão salvos como um resultado final e o próximo caso será calculado. Cancelar, as iterações continuarão enquanto todas as frequências ignoradas serão determinadas. O aviso será ignorado. A verificação de Sturm está desmarcada. A verificação de Sturm não é executada |
|
N |
ω * |
Inativo (devido ao limite superior ativo) |
Disponível somente para os solvers diretos e os métodos BLSI, SI e Lanczos. Não está disponível para o método de redução de base e todos os métodos de solver iterativo. A verificação de Sturm é executada no início dos cálculos, quando é obtido o número de frequências N1 que estão contidas entre zero e o limite superior: 0 < ω1 < ω2 < … < ωN1 < ω*
Em ambos os casos, é possível derivar vários pares próprios convergidos maiores do que N1, mas eles serão salvos como resultados finais somente quando: 0 < ω1 < ω2 < … < ωN1 < ω*. Todos os pares próprios convergidos que forem maiores do que ω* serão perdidos. |
|
N |
Inativo (devido a ativo do percentual de massa) |
Ativo: 0< percentual de massa<=100% |
Disponível para todos os métodos de solvers diretos. Não está disponível para o solver iterativo. Se o percentual de massa não for satisfatório, um prompt relevante será emitido. Nenhuma correção é executada. Caso contrário, os cálculos são executados da mesma maneira que no primeiro caso. |
Sísmico
Esse modo somente está disponível para os solvers diretos esparsos ou de horizonte.
Nas análises sísmica e espectral, não é importante usar pares próprios ordenados sequencialmente, já que somente devem ser levados em conta os pares próprios que contribuem consideravelmente para a resposta sísmica (uma vez que apresentam um fator de participação de massa significativo). Portanto, a verificação de Sturm não é executada.
O método Lanczos normalmente garante a convergência de um número de pares próprios consideravelmente maior do que N pares próprios na ordem de aumento sequencial. Quando os valores próprios ignorados precisam ser restaurados, é necessário obter um número de frequências convergidas consideravelmente maior do que as primeiras N frequências desejadas. Por exemplo, é comum que o método Lanczos produza as seguintes frequências convergentes.
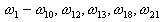
Quando o usuário precisar dos pares próprios sequencialmente ordenados, obterá somente os 10 primeiros. Os últimos 4 pares próprios são simplesmente descartados, assim como a contribuição de massa da correspondência. A essência do modo “Sísmico” proposto é levar em conta todos os pares próprios convergidos (não apenas os primeiros pares próprios sequenciais). Isso garante uma maior soma de massas em comparação com o modo “Modal”.
Métodos disponíveis: método Lanczos.
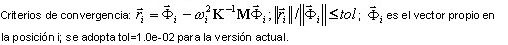
Os limites superiores são ignorados.
A porcentagem de massa atual é um valor médio de M%x, M%y, M%z para problemas 3D e um valor mínimo de M%x, M%z para problemas 2D (M%x, M%y, M%z são a soma atual das massas para a direção x, y, z, respectivamente). Essa estratégia é explicada pelo fato de que é geralmente muito difícil garantir uma porcentagem de massa suficiente para a direção vertical. É possível verificar a porcentagem de massa para cada direção nos resultados finais.
|
Nmodos |
Limites superiores |
Percentual de massa |
Comportamento do programa |
|---|---|---|---|
|
N |
Inativo |
Inativo (0) |
São calculados os N pares próprios não sequenciados. A verificação de Sturm não é executada. O número de pares próprios convergidos é igual a N. |
|
N |
Inativo |
Ativo: 0< percentual de massa<= 100% |
N é ignorado. Os cálculos continuam até que o percentual de massa atual não seja menor do que o percentual de massa exigida, até que o usuário seja solicitado a interromper os cálculos ou até que o número de pares próprios convergidos alcance o valor máximo disponível. Esse conjunto de valores é definido internamente e é 100 na versão atual. Após cada 20 etapas do método Lanczos, o número de pares próprios convergidos é recalculado e a porcentagem de massa atual é modificada. Um aviso solicita o percentual de massa obtido. Se indicado Sim, os cálculos continuarão durante as próximas 20 etapas do método Lanczos e essa mensagem será exibida novamente. Se a porcentagem de massa necessária não for alcançada (o número de pares próprios convergidos não ultrapassar o valor máximo disponível) Não, os pares próprios convergidos serão salvos como resultados finais e passados para o próximo caso. Cancelar, todos os avisos serão ignorados no futuro e os cálculos continuarão. |
Pseudomodo
Esse modo está disponível para os solvers diretos e iterativos. É recomendado somente para análises sísmica e espectral quando os modos modal e sísmico são muito demorados. Os modos modal e sísmico usam modos próprios como vetores de base para apresentar resposta sísmica e é possível exigir um número muito grande de modos próprios para assegurar uma soma suficiente de massas para alguns problemas difíceis. O pseudomodo rejeita essa ideia e gera as aproximações de Ritz para os pares próprios de nível mais baixo por meio dos vetores Lanczos para os solvers diretos ou dos métodos gradiente Ritz [8] e Lanczos modificado para os solvers iterativos. Essa é uma forma mais eficaz de operação na maioria dos casos, porque é necessário um número menor de vetores de base do que no modo modal. Isso foi demonstrado por E.L.Wilson [1-3]. O pseudomodo é semelhante aos vetores Ritz dependentes de carga, propostos em [1-3] e aplicados no SAP2000. Deve-se observar que a norma francesa PS-92 admite a aplicação de abordagens com base científica para adicionar sistemas de vetores de base aos modos próprios existentes, a fim de aumentar a soma das massas. Os detalhes da abordagem e a eficácia do pseudomodo são apresentados nos anexos 3B e 3C, respectivamente.
Os limites superiores são ignorados.
A porcentagem de massa atual é definida como um valor médio de M%x, M%y, M%z para problemas 3D e como um valor mínimo de M%x, M%z para problemas 2D (M%x, M%y, M%z são a soma atual das massas para a direção x,y,z, respectivamente). Essa estratégia é explicada pelo fato de que é geralmente muito difícil garantir uma porcentagem de massa suficiente para a direção vertical. É possível verificar a porcentagem de massa para cada direção nos resultados finais.
|
Nmodos |
Limites superiores |
Percentual de massa |
Comportamento do programa |
|---|---|---|---|
|
N |
inativo |
Inativo (0) |
Disponível para os solvers diretos e iterativos. São gerados N vetores de base para definir o subespaço de trabalho. São salvos N vetores de base para uso com análises sísmicas e espectrais. Esse regime é recomendado. |
|
N |
Inativo |
Ativo: 0< percentual de massa<= 100% |
Disponível somente para solvers diretos São gerados N vetores de base para definir o subespaço de trabalho. São salvos os vetores de base que sejam suficientes para satisfazer o percentual de massa específico. O número de vetores de base salvos será menor do que N se o percentual de massa for < 100% |
3.6. Análise espectral
O método de espectros de resposta é aplicado para as análises sísmica e espectral. Esse método consiste em decompor uma estrutura de múltiplos graus de liberdade (MDOF) em um sistema de osciladores de grau único de liberdade (SDOF). A resposta para cada um desses osciladores independentes e a soma estatística das respostas extremas para cada oscilador é calculada por meio dos métodos SRSS, CQC, 10% e soma dupla [3, 21].
Quando os modos modal ou sísmico são aplicados, os modos próprios definem esse sistema de osciladores de grau único de liberdade. Quando o pseudomodo é aplicado (consulte a seção 3.5), os vetores de base do pseudomodo definem esse sistema de osciladores de grau único de liberdade.
A introdução do pseudomodo requer uma nova abordagem em relação à avaliação de respostas de cada modo. A abordagem clássica é a seguinte:
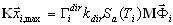 ( 3.1.1 )
( 3.1.1 )
em que K, M – matrizes de rigidez e de massa, Γ – fator de participação de massa, Sa – aceleração espectral, T – período, i – número do modo, k – coeficiente de escala do espectro, dir – índice de direção de movimento sísmico de entrada (dir = X,Y,Z), x – vetor de deslocamento da reação máxima do modo i.
Agora, a seguinte abordagem é aplicada (consulte o anexo B):
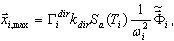 ( 3.1.2 )
( 3.1.2 )
em que 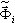 indica um vetor de base (não é necessário que
indica um vetor de base (não é necessário que 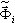 seja uma aproximação exata de
seja uma aproximação exata de 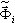 – vetor próprio exato de
– vetor próprio exato de 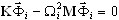 , ωi – aproximação do valor próprio exato Ωi. É possível demonstrar que (3.1.1) fornece exatamente a mesma solução
, ωi – aproximação do valor próprio exato Ωi. É possível demonstrar que (3.1.1) fornece exatamente a mesma solução 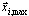 que (3.1.2), se
que (3.1.2), se 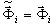 ( ωi = Ωi). No entanto, (3.1.2) é aplicável não apenas para os solvers diretos, mas também para o solver iterativo, uma vez que não exige o procedimento de resolução correspondente à matriz de rigidez K. Assim, é mais rápido do que (3.1.1) e permite controlar os resultados com mais segurança (soma das forças - soma das reações).
( ωi = Ωi). No entanto, (3.1.2) é aplicável não apenas para os solvers diretos, mas também para o solver iterativo, uma vez que não exige o procedimento de resolução correspondente à matriz de rigidez K. Assim, é mais rápido do que (3.1.1) e permite controlar os resultados com mais segurança (soma das forças - soma das reações).
A fórmula apresentada abaixo é obtida com base em (3.1.1)
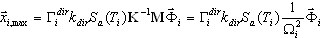 ( 3.1.3 )
( 3.1.3 )
O vetor de resposta modal 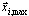 descreve a resposta extrema do oscilador de grau único de liberdade da correspondência. A próxima etapa deve ser dedicada à definição da resposta final da estrutura de múltiplos graus de liberdade por meio da média estatística entre os modos e entre as direções de entrada sísmica.
descreve a resposta extrema do oscilador de grau único de liberdade da correspondência. A próxima etapa deve ser dedicada à definição da resposta final da estrutura de múltiplos graus de liberdade por meio da média estatística entre os modos e entre as direções de entrada sísmica.
As versões anteriores do Robot permitem atribuir diversas direções de entrada sísmica estatisticamente independentes com seus próprios multiplicadores de escala em um único caso de carga. A média estatística entre direções é produzida por meio da soma dos valores absolutos e da raiz quadrada da soma das combinações de quadrados dentro de cada modo. As opções correspondentes são definidas em Preferências do trabalho.
A opção “soma dos valores absolutos” fornece o seguinte:
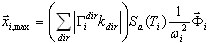 ( 3.1.4 )
( 3.1.4 )
A raiz quadrada da soma da opção de quadrados gera a média de 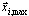 das direções correspondentes de movimento de entrada sísmica, como
das direções correspondentes de movimento de entrada sísmica, como 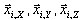 .
.
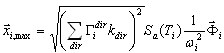 ( 3.1.5 )
( 3.1.5 )
É possível mostrar que cada componente de 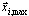 é a combinação SRSS de componentes de correspondência de
é a combinação SRSS de componentes de correspondência de 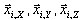
em que i = 1,2,...,N indica o número do modo ou do pseudomodo.
A combinação SRSS ou CQC entre modos (ou pseudomodos) é aplicada para obter a resposta final da estrutura considerada de MDOF após a média dos vetores de resposta modal 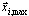 ter sido obtida, i = 1,2,...,N.
ter sido obtida, i = 1,2,...,N.
A média dos vetores de resposta modal 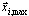 , i = 1,2,...,N será a mesma para a “soma dos valores absolutos” e a raiz quadrada da soma das opções de quadrados se a única direção de entrada sísmica tiver sido definida para o caso de carga atual (por exemplo, Kx=Kz=0, Ky=1).
, i = 1,2,...,N será a mesma para a “soma dos valores absolutos” e a raiz quadrada da soma das opções de quadrados se a única direção de entrada sísmica tiver sido definida para o caso de carga atual (por exemplo, Kx=Kz=0, Ky=1).
O Robot (versão 12.2 e posteriores) salva o procedimento mencionado acima do cálculo da média das respostas modais entre direções de entrada sísmica; no entanto, permite que seja executada a melhor abordagem. Recomenda-se definir uma única direção de entrada sísmica para cada caso de carga e, em seguida, aplicar a combinação SRSS entre direções (correspondente aos Guias regulamentares norte-americanos) ou as chamadas combinações de “Newmark” (correspondentes à Norma sísmica francesa PS-92 e ao Eurocódigo-8).
Vamos ilustrar os novos recursos no exemplo típico indicado abaixo.
Neste caso (movimento único de entrada sísmica para cada caso de carga), os valores típicos para multiplicadores de escala serão iguais
Kx=1; Ky=Kz=0 para dir = X (caso de carga S_X)
Kx=0; Ky=1; Kz=0 para dir = Y (caso de carga S_Y)
Kx=Ky=0; Kz=0,7 para dir = Z (caso de carga S_Z; a intensidade do movimento vertical é assumida como igual a 2/3 da intensidade do movimento horizontal)
Três casos de carga são definidos para cada movimento de entrada sísmica estatisticamente independente. A resposta modal para cada um será a mesma que em (3.1.2) (i = 1,2,...,N; dir = X,Y,Z).
Em seguida, é necessário definir o fator médio em todos os modos devido a cada direção de entrada sísmica: 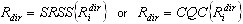
em que 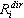 – algum fator (deslocamento, força, tensão etc.) para o modo de ordem i devido ao movimento de entrada sísmica na direção dir que corresponde à resposta modal
– algum fator (deslocamento, força, tensão etc.) para o modo de ordem i devido ao movimento de entrada sísmica na direção dir que corresponde à resposta modal 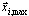 (obtida em (3.1.2));
(obtida em (3.1.2));
Rdir é o resultado da combinação SRSS ou CQC sobre todos os modos considerados (pseudomodos).
Em seguida, é produzida a média sobre todas as direções ativas de entrada sísmica de acordo com a opção escolhida.
Combinação SRSS:
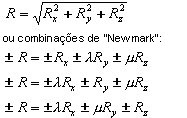
As opções de análise espectral permitem definir o espectro arbitrário do movimento de entrada sísmica.
3.7. Análise sísmica
O método de espectros de resposta é aplicado para as análises sísmica e espectral. A análise sísmica é executada com base na análise espectral (consulte a seção 3.6); no entanto, as acelerações espectrais Sa = Sa(Ti) são geradas para corresponder a uma norma sísmica selecionada, em vez de serem atribuídas pelo usuário (como é feito para a análise espectral).
A norma sísmica UBC-97 está disponível no Robot (versão 12.0 e posteriores). A análise do espectro de resposta é executada de acordo com as Seções 1631.5.1 – 1631.5.3 da Norma de construção uniforme de 1997 (Uniform Building Code). É possível atender aos requisitos da Seção 1631.5.4 (“Os parâmetros de resposta elástica podem ser reduzidos...”) por meio de mecanismos de combinação do Robot. Os componentes básicos de cisalhamento Vx, Vy, Vz, os componentes do momento de ultrapassagem Mx e My e o momento de torção Mz (presume-se que o eixo OZ seja vertical) são apresentados na tabela “Reações” na linha “Soma de forças”, tanto para cada resposta modal quanto para combinações SRSS e CQC entre modos.
As normas sísmicas a seguir estão disponíveis no programa:
- UBC97
- PS 69 R. 82
- AFPS
- PS 92
- RPA 88
- DM 16.1.96
- EC 8
- IBC 2000
- P100 92
- Norma turca
- Normas chinesas
- Norma argentina
- EAK 2000
3.8. Filtros seletivos
Somente os modos que têm um fator de participação de massa relativamente significativo contribuem de forma considerável para a resposta sísmica de uma estrutura. Portanto, basta levar em conta apenas esses modos. Os modos restantes, com fatores de participação de massa inferiores, podem ser ignorados durante a análise sísmica. Geralmente, o número de modos derivados é consideravelmente maior do que o número resultante da avaliação de porcentagem de massa. Portanto, o espaço em disco e o tempo de cálculo poderão ser salvos se apenas os modos com fatores de participação de massa significativos forem selecionados.
É possível usar dois métodos.
- Criar uma lista de modos aceitos para cada direção de entrada sísmica (caso sísmico) com base nos resultados obtidos anteriormente com a análise modal.
- Atribuir um valor de limite de massa para a porcentagem de massa modal (todos os modos com a porcentagem de massa modal abaixo desse limite serão ignorados).
A primeira forma é mais eficiente, embora exija uma análise modal prévia. A segunda forma permite que os filtros sejam aplicados na mesma execução com análises espectral e sísmica; no entanto, ela normalmente ocupa mais espaço em disco e envolve um maior esforço de cálculo.
Considere outro exemplo. Os resultados da análise modal são apresentados abaixo, na tabela 3.1, em que os casos sísmicos são definidos da seguinte maneira: Dir_X (Kx=1; Ky=Kz=0), Dir_Y (Kx=0; Ky=1; Kz=0) e Dir_Z (Kx=Ky=0; Kz=1)
Tabela 1
|
Número do modo |
Participação de massa UX (%) |
Participação de massa UY (%) |
Participação de massa UZ (%) |
Period |
|---|---|---|---|---|
|
1 |
0.05 |
12.01 |
0.004 |
0.803 |
|
2 |
67.43 |
0.06 |
0.005 |
0.705 |
|
3 |
0.002 |
0.08 |
0.07 |
0.686 |
|
4 |
0.001 |
0.008 |
0.009 |
0.650 |
|
5 |
25.4 |
0.07 |
2.06 |
0.590 |
|
6 |
0.09 |
68.5 |
5.05 |
0.540 |
|
7 |
0.08 |
10.3 |
0.06 |
0.490 |
|
8 |
0.07 |
0.06 |
0.56 |
0.460 |
|
9 |
0.05 |
0.07 |
30.56 |
0.420 |
|
10 |
0.08 |
0.06 |
0.25 |
0.380 |
|
11 |
0.06 |
0.01 |
26.7 |
0.270 |
Vamos supor que todos os modos com fatores de participação de massa maiores do que 1% sejam levados em conta. Os valores correspondentes de participação de massa são fornecidos na tabela. Observe que se as direções de entrada sísmica forem atribuídas como (1 0 0) para o caso Seism_X, os modos com valores de participação de massa significativos para as direções UY, UZ não contribuirão de forma alguma para a resposta sísmica (consulte a seção 3.6):
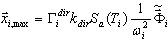
em que dir = X, Y, Z – direção sísmica de entrada; 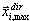 – resposta máxima do modo i;
– resposta máxima do modo i; 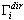 – fator de participação de massa; Sa(Ti) – aceleração espectral;
– fator de participação de massa; Sa(Ti) – aceleração espectral; 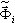 – vetor próprio de i ou vetor de base (no caso do pseudomodo). O multiplicador escalar no lado direito da fórmula acima
– vetor próprio de i ou vetor de base (no caso do pseudomodo). O multiplicador escalar no lado direito da fórmula acima 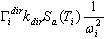 define a contribuição do modo i para a resposta sísmica da direção dir. Nesse caso, em que Ky = Kz = 0, as contribuições consideráveis são feitas pelos modos 2 e 5. Os modos restantes não contribuem para a resposta sísmica, devido ao multiplicador Kdir zero (dir = Y, Z) e a pequenos valores de participação de massa para a direção dir=X. Da mesma forma, é possível mostrar que, no caso de Dir_Y, basta levar em conta os modos 1, 6, 7; enquanto para o caso Dir_Z, devem ser considerados os modos 5, 6, 9, 11.
define a contribuição do modo i para a resposta sísmica da direção dir. Nesse caso, em que Ky = Kz = 0, as contribuições consideráveis são feitas pelos modos 2 e 5. Os modos restantes não contribuem para a resposta sísmica, devido ao multiplicador Kdir zero (dir = Y, Z) e a pequenos valores de participação de massa para a direção dir=X. Da mesma forma, é possível mostrar que, no caso de Dir_Y, basta levar em conta os modos 1, 6, 7; enquanto para o caso Dir_Z, devem ser considerados os modos 5, 6, 9, 11.
Portanto, por meio de filtros, o programa pode levar em conta somente os modos relevantes: 2 para o caso Dir_X, 3 para o caso Dir_Y e 4 para o caso Dir_Z. Isso ocorre sem uma perda significativa de contribuições de massa. É importante observar que se não usássemos os filtros seríamos forçados a aplicar os 11 modos para cada caso.
Essa abordagem permite reduzir o tempo de cálculo para problemas dinâmicos de larga escala (bem como os requisitos de espaço em disco e a quantidade de dados a serem pós-processados) sem redução significativa da precisão do resultado em comparação com o método tradicional (quando os filtros seletivos não são usados).
Por exemplo, o problema de larga escala PJG203 contém 34.266 equações (a largura de banda é igual a 990 após a otimização). O modelo FE correspondente é apresentado no anexo 3D. Consulte a Fig. A1. Devem ser calculados os 25 pares próprios com a matriz de massa consistente e três casos sísmicos. O tempo de cálculo ainda atinge aproximadamente 50 horas com um Pentium PRO (64 MB de RAM, 200 MHZ). O espaço em disco necessário ultrapassou 1 GB. Além disso, surgiu um problema com o módulo de projeto de aço, causado por espaço insuficiente em disco (para calcular as combinações SRSS e CQC, foi necessário armazenar os dados dos 25 modos multiplicados pelos 3 casos sísmicos abrangendo um grande número de graus de liberdade para todos os fatores: deslocamentos, forças internas, tensões). A aplicação de filtros seletivos permite que o programa resolva esse problema com êxito.
3.9. Análise harmônica
É produzida a seguinte definição de reação constante de uma estrutura à ação de uma carga harmônica única:
F(t) = F sin( ω t)
em que w é a pulsação da carga de excitação. O comportamento de uma estrutura é descrito como
(K - ω2 M) X = F,
em que X – valor de amplitude do vetor de deslocamento.
3.10. Análise do histórico no tempo
O método de decomposição modal (sobreposição) é executado no Robot. Baseia-se na representação de um movimento de estrutura como uma sobreposição do movimento de modos não acoplados. Portanto, o método exige que os valores próprios e os vetores próprios sejam determinados. O método Lanczos é recomendado para esta finalidade. O método de decomposição modal aproveita a redução de equações não acopladas. É uma abordagem apropriada para analisar a resposta dinâmica de estruturas sujeitas a ações de longo prazo de cargas dinâmicas (por exemplo, carga não regular causada pelo trabalho em equipamentos em linha ou ação sísmica). O contexto matemático e as particularidades de aplicação são apresentados em [3,4,6].
A equação (sem amortecimento) pode ter a seguinte forma:
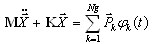 (3.11.1)
(3.11.1)
em Ng – número de “grupos de carga”, φk(t) – considerando o histórico de tempo para o grupo de carga k-th.
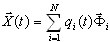 (3.11.2)
(3.11.2)
em que 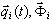 – correspondente ao modo e à coordenada da normal de ordem i (vetor próprio ou vetor Ritz). A substituição de (3.11.2) por (3.11.1) e a adição de termos de amortecimento geram as seguintes equações modais não acopladas [3,4,6]
– correspondente ao modo e à coordenada da normal de ordem i (vetor próprio ou vetor Ritz). A substituição de (3.11.2) por (3.11.1) e a adição de termos de amortecimento geram as seguintes equações modais não acopladas [3,4,6]
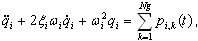 (3.11.3)
(3.11.3)
em que 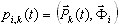 , ξi – parâmetro de amortecimento modal (normalmente ξi = 0,05 - 0,2; quando ξi = 1, indica amortecimento crítico – limite entre movimento de oscilação e movimento aperiódico), ωi – frequência de vibração natural (pulsação), i=1,2,...,N
, ξi – parâmetro de amortecimento modal (normalmente ξi = 0,05 - 0,2; quando ξi = 1, indica amortecimento crítico – limite entre movimento de oscilação e movimento aperiódico), ωi – frequência de vibração natural (pulsação), i=1,2,...,N
Cada uma das equações é resolvida numericamente. É aplicado o método de segunda ordem com seleção automática da etapa de integração. O vetor de deslocamento resultante para os pontos de tempo definidos t = t1, t2, ..., t5 é obtido por meio da substituição de qi(t5) em (3.11.2).
É possível aplicar o método de decomposição modal para a análise de resposta sísmica. Nesse caso, a equação de movimento tem a seguinte forma
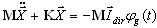
e as equações modais não acopladas apropriadas –
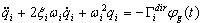 (3.11.5)
(3.11.5)
em que 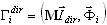 – fator de participação de massa para o modo de ordem i e a direção de entrada sísmica dir. Cada modo deve ser normalizado da seguinte forma:
– fator de participação de massa para o modo de ordem i e a direção de entrada sísmica dir. Cada modo deve ser normalizado da seguinte forma:  . Finalmente, todos os resultados (deslocamentos, velocidades, acelerações, forças internas, reações e outros) são armazenados somente para os pontos de tempo definidos t = t1, t2, ..., t5. O pós-processador de alto desempenho permite analisar o resultado da análise de histórico de tempo em modos de diagrama e de tabela. O modo de diagrama exibe os fatores selecionados (deslocamento, aceleração, velocidade, reações, forças de cisalhamento, momentos de dobra e outros) dos graus de liberdade (DOF) escolhidos e apresenta a forma deformada de uma estrutura no ponto de tempo selecionado. O modo de tabela permite não apenas que sejam exibidos os valores correspondentes, mas também pesquisar automaticamente os valores máximo e mínimo entre os fatores de resposta em todos os pontos de tempo armazenados.
. Finalmente, todos os resultados (deslocamentos, velocidades, acelerações, forças internas, reações e outros) são armazenados somente para os pontos de tempo definidos t = t1, t2, ..., t5. O pós-processador de alto desempenho permite analisar o resultado da análise de histórico de tempo em modos de diagrama e de tabela. O modo de diagrama exibe os fatores selecionados (deslocamento, aceleração, velocidade, reações, forças de cisalhamento, momentos de dobra e outros) dos graus de liberdade (DOF) escolhidos e apresenta a forma deformada de uma estrutura no ponto de tempo selecionado. O modo de tabela permite não apenas que sejam exibidos os valores correspondentes, mas também pesquisar automaticamente os valores máximo e mínimo entre os fatores de resposta em todos os pontos de tempo armazenados.
3.11. Análise modal com a consideração de forças estáticas
São consideradas as vibrações lineares de pequena escala com relação ao estado estático de equilíbrio induzido por uma carga estática determinada. Sabe-se que as forças estáticas têm influência nas frequências de vibração naturais. A análise modal habitual não considera essa influência; no entanto, a influência é considerada quando a análise modal leva em conta as forças estáticas.
As equações não lineares completas descrevem o movimento do estado de equilíbrio relativamente estático de um sistema, induzido pelas cargas estáticas fornecidas.
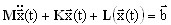 (3.12.1)
(3.12.1)
em que M, K – matrizes de massa e de rigidez, L(x(t)) – operador não linear, x(t), b – vetor de deslocamento e vetor de carga. O procedimento de linearização consiste no seguinte:
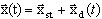 (3.12.2)
(3.12.2)
em que xst é uma parte da solução comum que descreve o estado de equilíbrio estático e xd (t) é um vetor de pequenos deslocamentos dinâmicos. O operador não linear pode ser apresentado como decomposição da série Taylor
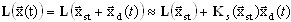 (3.12.3)
(3.12.3)
em que 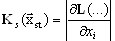 é uma matriz de tensão e rigidez, que é uma jacobiana e leva em conta a ação das forças estáticas. Portanto, resulta no seguinte:
é uma matriz de tensão e rigidez, que é uma jacobiana e leva em conta a ação das forças estáticas. Portanto, resulta no seguinte:
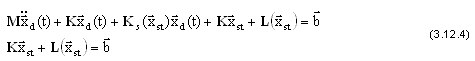
A primeira expressão é um resultado da linearização de deslocamentos dinâmicos apropriadamente pequenos (nota: 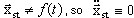 ) e a segunda descreve o estado de equilíbrio estático não linear. Portanto, o movimento dinâmico de pequena dimensão com relação ao estado de equilíbrio estático é da seguinte forma:
) e a segunda descreve o estado de equilíbrio estático não linear. Portanto, o movimento dinâmico de pequena dimensão com relação ao estado de equilíbrio estático é da seguinte forma:
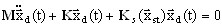 (3.12.5)
(3.12.5)
Vamos substituir xd (t) = Φ ei ω t. Um problema de valor próprio se origina de (3.12.5)
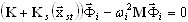 (3.12.6)
(3.12.6)
em que ωi – valor próprio; Φ i – vetor próprio.
Os cálculos são executados em dois estágios:
- Análise linear (3.12.7) ou não linear (3.12.8) do estado de tensão-deformação estática induzida por uma determinada carga estática
K x st = b (3.12.7)
K xst + L(xst ) = b, (3.11.8)
em que xst – vetor desconhecido de estado estático, b – vetor de forças estáticas determinadas (vetor de carga estática), K – matriz de rigidez, L (xst, b) – operador não linear. O vetor de carga estática b pode ser um resultado da combinação de várias cargas estáticas. Deve-se observar aqui que uma abordagem linear não satisfaz exatamente a equação de equilíbrio não linear (3.11.8). Portanto, o vetor xst para o estado de equilíbrio estático é o resultado de uma solução aproximada e a matriz de tensão e rigidez Ks (xst ) contém um erro. Se a estrutura considerada for suficientemente rígida e os efeitos não lineares parecerem reduzidos, essa aproximação parecerá estar correta. Caso contrário, será necessário resolver o problema estático não linear (3.11.8) (essa técnica não é abrangida no manual). Obviamente, a abordagem linear (3.2.17) é mais rápida do que a não linear (3.11.8). No caso da abordagem linear, acontece que Ks (xst) = G (xst ) = G, em que G é uma matriz de rigidez geométrica.
- Análise de valor próprio (3.12.6)
Os valores positivos de ωi (ωi > 0) são conhecidos por representar estados de equilíbrio estável, os valores negativos (ωi < 0) – valores instáveis, enquanto o valor zero (ωi = 0) corresponde à falta de estabilidade (flambagem).
A perda de definição positiva da matriz K + Ks (xst) significa que a carga estática ultrapassa seu valor crítico (flambagem). É emitido um aviso relevante. A convergência será perdida durante a execução do problema estático não linear (3.11.8). É recomendável interromper os cálculos porque os cálculos seguintes ainda não estão claros.
Somente a abordagem não linear está disponível para estruturas que contêm elementos de cabo e de tensão-compressão.
Por exemplo, consideremos a seguinte figura.
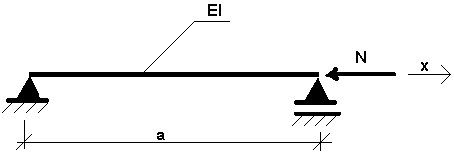
Fig. 3.11.1
Está presente o valor N – carga estática. A expressão a seguir descreve o comportamento de um sistema desse tipo:
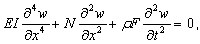 ( 3.11.9 )
( 3.11.9 )
em que: w – deslocamento da dobra, ρ – densidade do material, F – área da seção transversal.
A solução será pesquisada como
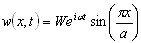 ( 3.11.10 )
( 3.11.10 )
Após a substituição de ( 3.11.10 ) por ( 3.11.9), resultará o seguinte:
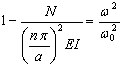 , ( 3.11.11 )
, ( 3.11.11 )
em que 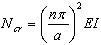 – carga de flambagem, ω0 – valor próprio de N = 0 (resultado da análise modal usual). Por fim,
– carga de flambagem, ω0 – valor próprio de N = 0 (resultado da análise modal usual). Por fim,
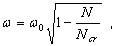 ( 3.11.12 )
( 3.11.12 )
em que ω – valor próprio do sistema sujeito à ação de uma carga estática N. Esse resultado é apresentado graficamente na Fig. 3.11.2:
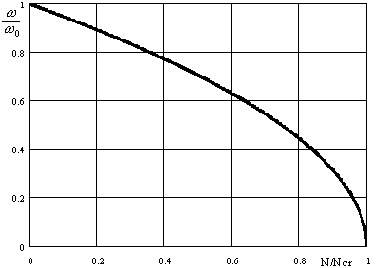
Fig. 3.11.2
Em uma estrutura real, normalmente a dependência ω = ω (λ), em que l é um parâmetro de carga, é mais complexa do que a situação apresentada na expressão (3.11.12) (consulte [1,22]).
Anexo 3A
Métodos de solução de problemas de valor próprio
Observe que não existe atualmente um método ideal universal para a resolução de um problema de valor próprio.
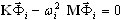 , i=1,2,...,n ( A1 )
, i=1,2,...,n ( A1 )
em que K é a matriz de rigidez, M é a matriz de massa, ![]() é o modo próprio e ωi é a pulsação. Para a maioria dos problemas, esse método usa menos recursos (tempo de cálculo e armazenamento em alta definição) do que qualquer outro. No entanto, não exclui situações diferentes no caso de outras tarefas. É recomendável aplicar outro método. A versão atual do Robot aborda diversos métodos para a resolução de um problema de valor próprio generalizado (A1). Cada um deles envolve suas próprias vantagens e desvantagens. Abaixo, apresentamos algumas recomendações a serem consideradas ao escolher um método de análise. Esperamos que, na maioria dos casos, estas sugestões permitam alcançar os resultados necessários da melhor forma.
é o modo próprio e ωi é a pulsação. Para a maioria dos problemas, esse método usa menos recursos (tempo de cálculo e armazenamento em alta definição) do que qualquer outro. No entanto, não exclui situações diferentes no caso de outras tarefas. É recomendável aplicar outro método. A versão atual do Robot aborda diversos métodos para a resolução de um problema de valor próprio generalizado (A1). Cada um deles envolve suas próprias vantagens e desvantagens. Abaixo, apresentamos algumas recomendações a serem consideradas ao escolher um método de análise. Esperamos que, na maioria dos casos, estas sugestões permitam alcançar os resultados necessários da melhor forma.
O método de iteração de subespaço (SI) é realizado exatamente como descrito em [4]; portanto, a descrição desse método não está incluída aqui.
Lanczos
O método Lanczos [12,16,17] é uma abordagem robusta e muito eficaz usada para resolver problemas de valor próprio em larga escala (A1). Está disponível quando são selecionados solvers de linha do horizonte ou direto esparso.
Essa abordagem localiza os primeiros n valores próprios e modos próprios necessários com qualquer precisão desejada. Quanto maior for o número de pares próprios necessários, mais vantajoso será o método Lanczos. No entanto, a abordagem envolve várias limitações.
A matriz tridimensional T não deve ser decomposta. Não é possível analisar uma estrutura que consista em duas ou mais subestruturas não conectadas. Nesse caso, cada subestrutura é considerada separadamente ou outra abordagem é implementada (por exemplo, os métodos de iteração de subespaço do bloco (BLSI) ou de redução de base).
A matriz de massa M deve ser considerada como fragmentada com rotações ou consistente.
Não é permitida a densidade zero.
O método Lanczos usa a redução para a matriz tridimensional T
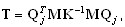 , ( A2 )
, ( A2 )
em que Qj = {q1, q2, …, qj} – a matriz retangular Neq x j e Neq é o número de equações, j – número de etapas “Lanczos”, qj – vetor Lanczos j-th. A expressão
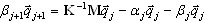 ( A3 )
( A3 )
gera o próximo vetor Lanczos qj+1 e define a linha atual da matriz T
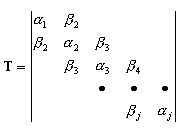
Portanto, é obtido o seguinte problema de valor próprio reduzido:
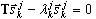 , k=1,2,...,j ( A4 )
, k=1,2,...,j ( A4 )
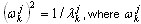 é a aproximação j-th para ωk, k=1,2,...,n, n é o número necessário de pares próprios. O algoritmo continuará os cálculos (para aumentar o j– número de etapas Lanczos), até que a precisão necessária seja alcançada para todos os valores próprios necessários.
é a aproximação j-th para ωk, k=1,2,...,n, n é o número necessário de pares próprios. O algoritmo continuará os cálculos (para aumentar o j– número de etapas Lanczos), até que a precisão necessária seja alcançada para todos os valores próprios necessários.
O procedimento seletivo de ortogonalização suporta o nível necessário de ortogonalidade entre os vetores Lanczos qj, o que garante a segurança e a estabilidade numérica do processo de cálculo. Empregamos métodos econômicos para fornecer ortogonalização seletiva e para resolver o problema de valor próprio reduzido (A4) por meio de iterações de QR duplas com deslocamentos.
Os vetores próprios de origem são determinados pela seguinte fórmula
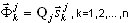 ( A5 )
( A5 )
Os detalhes são apresentados em [12,16,17].
Método de redução de base
Esse método [4, 5] é conhecido como o método aprimorado Rayleigh-Ritz [4]. Em [5], um método desse tipo apresenta uma variante discreta do método Bubnov-Galerkin. Esse algoritmo permitirá obter valores aproximados dos primeiros pares próprios se algumas informações sobre eles forem conhecidas. Esse método requer a atribuição de um grau de liberdade principal (MDOF) para obter o sistema reduzido. Dessa forma, é possível controlar o processo de criação do modelo reduzido. Essa é uma ferramenta muito eficaz para quem tem experiência na análise dinâmica de estruturas e lida com o mesmo tipo de estruturas, cujo comportamento é conhecido. Esse método permite a exclusão de graus de liberdade (DOF) indesejados do modelo reduzido e reduz o problema complexo inicial com um grande número de DOFs para uma forma reduzida. Isso é obtido com um número consideravelmente menor de graus de liberdade. A experiência com a análise dinâmica de estruturas demonstra que o usuário pode enfrentar alguns problemas quando os métodos de redução automática (BLSI, SI e Lanczos são levados em conta) geram um processo de cálculo muito complexo. Por exemplo, os modos de vibração local de barras únicas podem provocar problemas sérios, já que o processo de cálculo procura os pares próprios automaticamente sem nenhuma seleção. Isso deve ser observado na maioria dos casos de estruturas reais. Caso contrário, essas vibrações locais serão limitadas por algumas restrições não levadas em conta no modelo FEM, ou sua contribuição não será essencial para o movimento geral do sistema. Normalmente, a porcentagem de massa é muito pequena para essas vibrações locais. Neste caso, o uso de métodos exatos provoca as dificuldades mencionadas. No entanto, a implementação do método aproximado de redução de base pode simplificar consideravelmente o processo de cálculo.
Esse método tem as seguintes limitações.
O usuário deve atribuir o MDOF: os nós principais e as direções principais. Presume-se que somente deslocamentos (e não rotações) possam ser atribuídos como graus de liberdade principais.
O algoritmo é implementado para qualquer tipo de matriz de massa; no entanto, o tipo de matriz de massa fragmentado sem rotações é mais vantajoso com relação ao tempo de cálculo.
- A verificação da sequência Sturm não está disponível. Existe somente uma forma de verificar a convergência. Aumente o número de MDOF (atribua outros nós e direções principais), resolva este problema mais uma vez e compare os valores próprios.
Esse método transforma o problema de valor próprio de grande escala de origem do modelo FEM
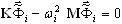 (A6)
(A6)
(A1) no problema de valor próprio do modelo reduzido
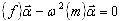 (A7)
(A7)
em que {f} – a matriz de influência, {m} – a matriz de massa generalizada para um modelo reduzido,
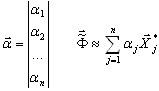 (A8)
(A8)
Em que n é um número de graus de liberdade de um modelo reduzido. A base para tais transformações é uma solução estática obtida para os estados de unidade apropriados: as forças nodais de unidade são aplicadas consequentemente em cada nó principal, na direção principal selecionada. Um problema estático de larga escala é resolvido para n lados direitos:
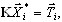 i = 1, 2, ..., n (A9)
i = 1, 2, ..., n (A9)
em que Ti – vetor de carga que corresponde a i – carga de unidade. O usuário deve atribuir nós principais e direções principais. Todas as operações exigidas serão executadas pelo programa.
O problema de valor próprio reduzido é resolvido pelo método de Jacobi, que gera as frequências aproximadas ωi e os modos 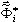 , i=1,2,...,n. Os detalhes dessa abordagem são apresentados em [5].
, i=1,2,...,n. Os detalhes dessa abordagem são apresentados em [5].
Método de iteração de subespaço do bloco
O método de iteração de subespaço do bloco (BLSI) soluciona um problema de valor próprio generalizado (A1). Está disponível para solvers diretos esparsos e de linha do horizonte. É uma abordagem avançada e muito eficaz. A aplicação desse método é altamente recomendada quando surge um problema de larga escala e é necessário obter um grande número de pares próprios (mais de 10). É possível aplicar o método BLSI para a análise de estruturas separadas. Durante a análise modal, estão disponíveis todos os tipos de matrizes de massa (fragmentado sem rotações, fragmentado com rotações e consistente). A área de aplicação dessa abordagem é limitada pelo modo modal. Os modos sísmico e o pseudomodo ainda estão disponíveis se for escolhido o método Lanczos.
A verificação da sequência Sturm é executada para detectar os valores próprios ignorados. O método BLSI controla a continuidade de valores próprios convergidos. A descontinuidade de valores próprios convergidos indica a presença de valores próprios ignorados. No entanto, a continuidade de valores próprios convergidos não fornece uma garantia estrita de que não existam valores próprios ignorados. Contudo, os resultados de vários cálculos indicam que, na maioria dos casos, as verificações da sequência Sturm não detectam valores próprios ignorados quando o método BLSI garante a continuidade da convergência. A grande vantagem desse método será a possibilidade de evitar o demorado procedimento de verificação de Sturm se não for necessária uma garantia completa da ausência de valores próprios ignorados. Se a descontinuidade dos valores próprios convergidos for identificada, será exibida a seguinte mensagem (consulte a Fig. A1).
A ideia principal do método BLSI [1-3] consiste em iterações de vetores simultâneas no subespaço de tamanho fixo. Cada vetor convergido é removido do subespaço de trabalho (bloco) e, em seu lugar, é adicionado um novo vetor inicial. A ortogonalidade dos vetores convergidos é garantida em cada etapa da iteração.
A aplicação do procedimento de aceleração por deslocamento [1,4] é recomendada durante a análise modal quando ocorre convergência lenta.
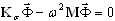 , ( A10 )
, ( A10 )
em que Kσ= K - σ M, σ – valor de deslocamento. No início da análise, é assumido que σ = 0. Se novos valores próprios convergidos não aparecerem no número aceito de etapas de iteração de controle, será feita a atualização automática do valor de deslocamento. Por exemplo, consideremos que o número de etapas de controle é igual a 5. Em seguida, 5 valores próprios convergidos aparecem após 4 iterações. O valor de deslocamento permanece σ = 0. Na próxima etapa de iteração, 3 valores próprios convergem. O valor de deslocamento permanece σ = 0. Em seguida, durante 5 etapas de iteração, não há convergência de nenhum modo próprio. O algoritmo detecta “convergência lenta” novamente, assume que σ = ω8 2, atualizaKσ = K - σ M e fatora a matriz deslocada atualizada Kσ. Em seguida, depois de 2 etapas de iteração, 2 modos próprios convergem. O valor de deslocamento permanece como ω8 2. Depois, durante as 5 etapas de iteração a seguir, não ocorre nenhuma convergência de valores próprios. O algoritmo detecta novamente uma “convergência lenta” e assume que ω10 2 , atualiza Kσ = K - σ M e fatora a matriz deslocada atualizada Kσ.
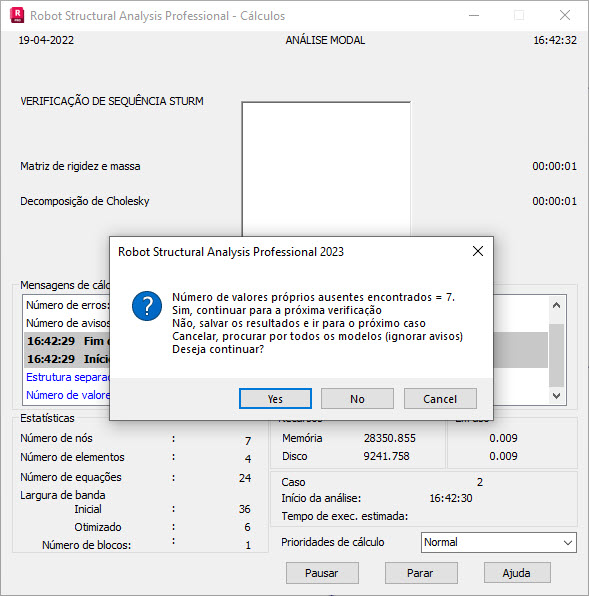
Fig. A1 A descontinuidade dos valores próprios convergidos é detectada ao executar o método BLSI.
Se indicado:
- Sim, os cálculos continuarão até que apareça o próximo valor próprio convergido. Depois, é executada a próxima verificação.
- Não, os resultados serão salvos e os cálculos passarão para o próximo caso.
- Cancelar, os cálculos continuarão enquanto for garantida a continuidade completa dos valores próprios convergidos. O aviso será ignorado.
Essas não são todas as recomendações. É possível aplicar ou não as acelerações por deslocamento. Lembre-se de que a aplicação do deslocamento adequado é uma ferramenta muito eficaz de aceleração de convergência. Caso contrário, cada fatoração da matriz atualizada Kσ pode ser um procedimento demorado, especialmente para um problema de larga escala. Portanto, a decisão final sobre a aplicação do deslocamento deve ser tomada com base na experiência e na intuição do usuário.
O exemplo a seguir ilustra o benefício da aplicação do deslocamento. O modelo de cálculo é mostrado na Fig. A2. Existem 50 modos próprios extraídos pelo método BLSI. O solver de linha do horizonte está selecionado. A tolerância 1.0e-09 é aceita. Acontece que a convergência que começa com o modo 38 ainda é tão lenta que, durante 20 minutos de cálculos, nenhum resultado é obtido. Quando a aceleração por deslocamento tiver sido ativada (a atualização de um deslocamento foi aceita em cada uma das cinco etapas de iteração não convertidas), o tempo de cálculo ainda será de 50 segundos. Obviamente, é possível apresentar vários exemplos de quando a aplicação do deslocamento reduz o número de iterações; no entanto, o tempo de cálculo aumenta. Recomendamos a ativação de acelerações por deslocamento quando uma abordagem convencional (os deslocamentos estão desativados) provoca um grande número de iterações em alguns estágios da execução do método BLSI.
Fig. A2 Estrutura do quadro espacial
Método Lanczos modificado
Esse é um ajuste do método Lanczos no pseudomodo para o solver iterativo. O método Lanczos usual exige a fatoração de uma matriz de rigidez (consulte A3). Quando um problema de larga escala é encontrado, a fatoração da matriz de rigidez ainda é muito demorada. No caso de grandes problemas (mais de 100.000 equações), para além de ser necessário um enorme esforço de cálculo para a fatoração de uma matriz de rigidez, a solução de um conjunto de equações de matriz devidamente fatorada também é cara.
O método Lanczos modificado baseia-se na abordagem iterativa. Evita o armazenamento, a montagem e a fatoração de uma matriz de rigidez de larga escala. A avaliação de cada vetor Lanczos exige aproximadamente o mesmo esforço de cálculo que a solução de um problema estático com um único lado direito. Em relação ao pseudomodo, ele reduz o número necessário de vetores Lanczos em comparação com o modo modal, que é aplicado ao executar o método Lanczos modificado.
O solver iterativo AEBEIS (consulte [7,8]) é aplicado para a geração de vetores Lanczos. Recomenda-se usar a técnica ICCF (fatoração Cholesky incompleta) para o pré-condicionamento de agregação multinível [7,8,18-20] e não multinível usual. Isso garante operações rápidas durante as avaliações de produtos de vetor-matriz e a resolução rápida do pré-condicionamento da correspondência. Deve-se observar que a tolerância adotada para o solver iterativo (Preferências do trabalho > Análise de estrutura > Parâmetros) determina a precisão da avaliação dos vetores Lanczos. Normalmente, é suficiente aceitar 1.0e-04. Quanto maior for o número de modos, mais próximos estarão os vetores Ritz inferiores dos modos próprios correspondentes, e será obtida uma soma mais completa das massas modais.
Método de gradiente de conjugado pré-condicionado (PCG)
O método PCG [9-13] é recomendado para a definição de um pequeno número de modos próprios no modo modal quando o solver iterativo é aplicado. Pode ser muito útil para atribuir uma carga de vento ou para verificar alguns modos de nível inferior obtidos pelo método PCG_Ritz. Estão disponíveis todos os tipos de pré-condicionamento (consulte Ferramentas > Preferências do trabalho > Iterativo > Parâmetros) definidos para a análise estática. É possível usar todos os tipos de matriz de massa (consistente, fragmentado com rotações e fragmentado sem rotações).
O método de gradiente conjugado pré-condicionado baseia-se na minimização direta do quociente Rayleigh
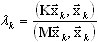 (A11)
(A11)
por meio da abordagem de gradiente, em que: k – número de iteração, λk – a aproximação correspondente de um valor próprio. A abordagem de gradiente procura esse valor do parâmetro αk, que assegura o valor mínimo de λk em (A11):
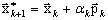 (A12)
(A12)
em que pk é um vetor de direção conjugada. A pesquisa do valor apropriado de αk [consulte 9-13] resulta em:
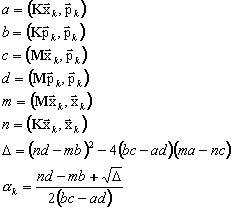
O pré-condicionamento B é aplicado para acelerar a convergência
B zk+1 = rk+1 -> zk+1 (A13)
A direção do gradiente é definida como
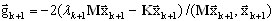 (A14)
(A14)
A nova direção conjugada é definida como
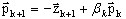 (A15)
(A15)
em que 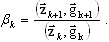
As iterações são executadas até
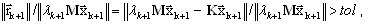 (A16)
(A16)
em que tol é a tolerância desejada. Normalmente, tol = 1.0e-02 garante uma precisão muito boa para fins de engenharia. É importante lembrar que o coeficiente de convergência (A16) é calculado com uma norma muito rígida (consulte a seção sobre a precisão dos cálculos). A tolerância mencionada acima fornece precisão de valores próprios que não é inferior a 1.0e-04.
Quando um primeiro par próprio é convergido, fica armazenado como um resultado final e as iterações começam a calcular o próximo. O procedimento de ortogonalização dos vetores próprios previamente definidos em cada etapa de iteração é empregado para evitar a duplicação de pares próprios. Esse processo é aplicado até serem obtidos todos os pares próprios desejados.
A forma mais eficiente de aceleração de convergência para o método PCG é a implementação de um bom pré-condicionamento. Todos os tipos de pré-condicionamento apresentados para um solver iterativo estão disponíveis para o método PCG. É altamente recomendável aplicar o pré-condicionamento multinível [18-20] ou não multinível com a regularização de ICCF [9-12] do solver AEBEIS [7,8].
Método gradiente Ritz (PCG_Ritz)
O PCG_Ritz [8] é um método rápido de definição de um conjunto de vetores Ritz no pseudomodo quando o solver iterativo está selecionado. Essa abordagem pode ser muito proveitosa para a análise sísmica e espectral de estruturas de médio porte, incluindo (10.000 – 60.000) equações.
Baseia-se na geração do sistema ortogonal de vetores de base. A abordagem de gradiente com pré-condicionamento de agregação multinível com base na técnica de elemento a elemento é aplicada para minimizar o quociente de Rayleigh para cada etapa de preparação do vetor de base. Isso garante a evolução do vetor de base resultante para o modo próprio de nível mais baixo sem agregação e decomposição de uma matriz de rigidez de larga escala. Esse método é frequentemente mais eficaz para a análise de resposta dinâmica em comparação com o método de sobreposição modal clássico, especialmente para a análise de resposta sísmica. O método proposto permite aplicar tipos arbitrários de elementos finitos devido à abordagem de agregação e garante uma solução rápida e um requisito barato em relação ao armazenamento em disco, em decorrência do uso do EBE. Esse método é particularmente eficaz quando é usada a matriz de massa consistente.
O problema de valor próprio fornecido é o seguinte:
Kφ - λM φ = 0 (A17)
em que K, M são as matrizes de rigidez e de massa respectivamente, φ é o vetor próprio e λ é o valor próprio. Será descrito o procedimento de evolução do conjunto de vetores de base x0, x1, ..., xn para o modo próprio de nível mais baixo. A abordagem de gradiente pré-condicionado é aplicada para minimizar o quociente de Rayleigh
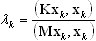 (A18)
(A18)
em que 0 ≤ k ≤ n, k é o número da etapa de evolução; n+1 é o número de vetores de base, que define o tamanho do vão do subespaço pertencente a (x0, x1, ..., xn); n+1 << N, em que N é o número de graus de liberdade para o problema considerado (A17). Com muita frequência, o problema do valor próprio considerado está mal condicionado. Nesse caso, a evolução do vetor de base resultante xk para o modo próprio de nível mais baixo será muito lenta. O operador de pré-condicionamento B é aplicado para melhorar tal situação. A expressão B zk = rk -> z k indica a resolução de um determinado conjunto de equações do vetor de correspondência zk, em que B é um operador de pré-condicionamento e rk = Kx k - λk M xk é um vetor residual correspondente.
Os vetores de base satisfazem as seguintes condições de ortogonalidade:
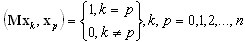 (A19)
(A19)
O problema de valor próprio de larga escala (A17) é reduzido para o problema de valor próprio de subespaço
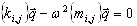 (A20)
(A20)
As matrizes de projeção de subespaço são definidas como {kij} = {Kxi, xj} e {mij} = {Mxi, xj} = U, em que U é uma matriz de unidade.
Os vetores Ritz v1, v2, ..., vn+1 para os vetores de base derivados x0, x1, ..., xn e as aproximações correspondentes de frequências ω1, ω2, …, ωn+1 são usados para sobreposição da resposta dinâmica estrutural.
O procedimento da evolução dos vetores de base xk, k = 0, 1, ..., n para o modo próprio de nível mais baixo está muito próximo da etapa correspondente do método de iteração de gradiente pré-condicionado para a solução de problema de valor próprio. É um fato bem conhecido que a convergência dos métodos de iteração pré-condicionada depende consideravelmente das propriedades do operador pré-condicionado B. Esse operador deve ser definido positivamente; ele permite uma solução de baixo custo B zk+1 = rk+1 e cumpre o número da condição C ( B-1 K) -> 1 da melhor maneira possível.
O último requisito no caso do método gradiente Ritz garante uma boa aproximação da parte inferior dos modos próprios.
Esse método está disponível somente para a abordagem iterativa multinível, o que garante uma boa qualidade de pré-condicionamento. Tanto a técnica de pré-condicionamento EBE (elemento a elemento) quanto a técnica ICCF são usadas. A qualidade dos vetores Ritz gerados dessa forma depende consideravelmente das propriedades do operador de pré-condicionamento B (consulte A13 e [8]). Como o modelo de nível de baixa resolução se aproxima bem dos modos de baixa vibração, os vetores Ritz no nível de alta resolução representam uma boa aproximação dos vetores próprios correspondentes (consulte [8]). Portanto, a qualidade dos resultados obtidos usando esse método depende consideravelmente da capacidade do modelo de nível de baixa resolução para manter a semelhança com o modelo FEM fornecido (conhecido como nível de alta resolução). Normalmente, um único nível de agregação garante uma boa aproximação. Quando o número de níveis de agregação for maior do que um, a qualidade dos resultados não será garantida. Trata-se da principal limitação da aplicação desse método para a análise de um problema de larga escala, quando o número de equações ultrapassa ~60.000.
Se a matriz de pré-condicionamento for B = K (o nível de baixa resolução é idêntico ao nível de alta resolução), o método gradiente Ritz proposto passará exatamente para o método Lanczos (consulte [8]). O contexto matemático é apresentado em [8].
Análise modal – Precisão dos cálculos
O problema de valor próprio generalizado é definido como
Kφ - λM φ = 0 (A17)
em que K, M são as matrizes de rigidez e de massa respectivamente, {φ, λ} – pares próprios (modo de vibração natural e valor próprio). São definidos dois tipos de vetores residuais:
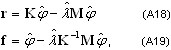
em que {φ, λ} são realmente pares próprios calculados que contêm alguns erros de cálculo. A primeira expressão define o vetor residual em termos de forças e a segunda em termos de deslocamentos.
São usados quatro critérios diferentes para estimar o erro de cálculo de vetores próprios.
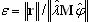 . Esse é um critério muito rigoroso. Normalmente, ε ≤ 0,01 significa que os primeiros quatro dígitos no valor próprio são definidos exatamente. Isso é aplicado somente para o método PCG, quando está selecionado o solver iterativo.
. Esse é um critério muito rigoroso. Normalmente, ε ≤ 0,01 significa que os primeiros quatro dígitos no valor próprio são definidos exatamente. Isso é aplicado somente para o método PCG, quando está selecionado o solver iterativo. - e = (r, φ). Esse é um critério um pouco mais brando do que o anterior. É aplicado para o método Lanczos modificado, quando está selecionado o solver iterativo.
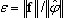 . Trata-se de um critério brando porque a convergência dos deslocamentos em uma determinada realização de FEM é normalmente mais rápida do que a convergência das forças internas. É usado para os métodos BLSI, SI e Lanczos, quando estão selecionados os solvers direto esparso e de linha do horizonte.
. Trata-se de um critério brando porque a convergência dos deslocamentos em uma determinada realização de FEM é normalmente mais rápida do que a convergência das forças internas. É usado para os métodos BLSI, SI e Lanczos, quando estão selecionados os solvers direto esparso e de linha do horizonte. 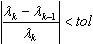 , em que λk, λk-1 são dois valores próprios sucessivos nas etapas de iteração k, k-1 e tol indica a tolerância dos valores próprios, definida na caixa de diálogo Parâmetros de análise modal. Isso é usado como critério intermediário enquanto os seguintes métodos estão sendo executados: BLSI, SI e Lanczos (solvers de linha do horizonte ou direto esparso) no modo modal. Esse critério não é robusto, mas é muito rápido. O uso de (4) permite reduzir consideravelmente o tempo de cálculo para os métodos BLSI, SI, Lanczos, especialmente em problemas de grande escala. Quando uma análise de valor próprio é concluída, o critério (3) é aplicado como a verificação final de precisão. O usuário deve examinar a coluna “Precisão” na tabela onde o valor
, em que λk, λk-1 são dois valores próprios sucessivos nas etapas de iteração k, k-1 e tol indica a tolerância dos valores próprios, definida na caixa de diálogo Parâmetros de análise modal. Isso é usado como critério intermediário enquanto os seguintes métodos estão sendo executados: BLSI, SI e Lanczos (solvers de linha do horizonte ou direto esparso) no modo modal. Esse critério não é robusto, mas é muito rápido. O uso de (4) permite reduzir consideravelmente o tempo de cálculo para os métodos BLSI, SI, Lanczos, especialmente em problemas de grande escala. Quando uma análise de valor próprio é concluída, o critério (3) é aplicado como a verificação final de precisão. O usuário deve examinar a coluna “Precisão” na tabela onde o valor 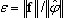 é apresentado. Se for identificada precisão insuficiente para um modo próprio, será necessário repetir a análise de valor próprio com uma tolerância maior para os valores próprios tol.
é apresentado. Se for identificada precisão insuficiente para um modo próprio, será necessário repetir a análise de valor próprio com uma tolerância maior para os valores próprios tol.
A tabela a seguir resume as considerações mencionadas acima. O símbolo N/A significa que a verificação de convergência correspondente não é produzida. Os resultados da verificação final são obtidos somente uma vez e são apresentados na coluna “Precisão” da tabela. A verificação de convergência durante os cálculos é executada várias vezes.
|
Solvers diretos |
Solver iterativo |
||||
|---|---|---|---|---|---|
|
Tipo de critério |
BLSI, SI, método Lanczos |
Método de redução de base |
Lanczos modificado |
PCG_Ritz |
PCG |
|
Durante os cálculos |
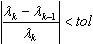
|
N/D |
N/D |
N/D |
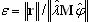
|
|
Verificação final |
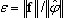
|
N/D |
e = (r, j) |
N/D |
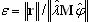
|
Observe que o método Lanczos para o modo sísmico produz verificação de convergência 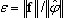 em cada uma das 20 etapas de Lanczos. O método de redução de base e o método PCG_Ritz são os métodos Ritz. Como não se trata de uma abordagem iterativa, a verificação da precisão não será executada.
em cada uma das 20 etapas de Lanczos. O método de redução de base e o método PCG_Ritz são os métodos Ritz. Como não se trata de uma abordagem iterativa, a verificação da precisão não será executada.
Se a precisão de alguns modos após o cálculo parecer insuficiente, será necessário o seguinte:
|
Solvers diretos |
Solver iterativo |
|||
|---|---|---|---|---|
|
BLSI, SI, método Lanczos – modo modal |
Método de redução de base |
Lanczos modificado |
PCG_Ritz |
PCG |
|
Diminuir a tol na caixa de diálogo Parâmetros de análise modal |
Aumentar o número de nós de base e direções de base |
Aumentar o número de modos Diminuir a tol na caixa de diálogo Parâmetros de solver iterativo |
Aumentar o número de modos Diminuir o número de níveis de agregação Aumentar o número de iterações internas |
Diminuir a tol na caixa de diálogo Parâmetros de análise modal |
Anexo 3B
Abordagem do pseudomodo
As equações de movimento de origem para cargas sísmicas assumem a seguinte forma:
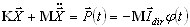 (B1)
(B1)
K, M – as matrizes de rigidez e de massa
I dir – vetor de unidade de direção; φ(t) – histórico de tempo da aceleração do solo
A solução é pesquisada como:
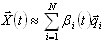 (B2)
(B2)
em que qi são os vetores de base do tamanho Neq – número de equações do modelo FE de origem.
Esses vetores devem satisfazer os seguintes requisitos:
- cinemática e condições de limite estático
- independência linear
- integridade da base
É possível adotar vetores Lanczos ou quaisquer vetores obtidos para forças nodais concentradas da unidade (método de redução de base para solvers diretos ou método gradiente Ritz PCG_Ritz).
A projeção de subespaço é descrita como:
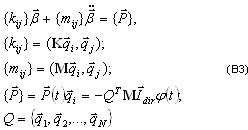
Observe que β é do tamanho N; a matriz Q é do tamanho NeqxN.
As equações de subespaço (B3) serão resolvidas por meio da decomposição dos vetores próprios (no subespaço definido por Q = {q1, q2, ..., qN}).
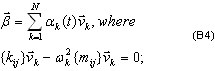
Observe que a decomposição (4) é uma expressão exata, porque o subscrito k assume valores de 1 a N, em todo o tamanho do subespaço Q.
A substituição de (B4) por (B3) gera o conjunto de equações não acopladas
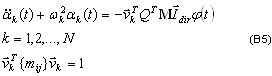
Consideremos
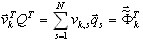 (B6)
(B6)
Portanto, (B5) pode ser apresentado como
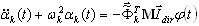 (B7)
(B7)
em que k=1,2,...,N.
Vamos aplicar o método de espectros de resposta às equações não acopladas (B7)
 (B8)
(B8)
em que 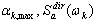 é a resposta máxima para o modo do subespaço k e a função de aceleração espectral, respectivamente.
é a resposta máxima para o modo do subespaço k e a função de aceleração espectral, respectivamente.
Vamos substituir (B8) por (B4) e depois por (B2):
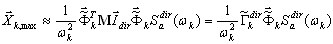 (B9)
(B9)
Deve-se observar que quando N -> Neq:
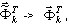
ωk -> Ωk
em que Ωk, 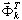 é o par próprio exato do problema de valores próprios dos FEs de origem
é o par próprio exato do problema de valores próprios dos FEs de origem
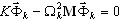 (B10)
(B10)
e 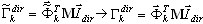 , em que
, em que 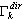 é o fator de participação de massa para o modo próprio k.
é o fator de participação de massa para o modo próprio k.
Conclusões
- A abordagem proposta não requer as aproximações “boas”
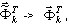 , ωk -> Ωk. É possível que
, ωk -> Ωk. É possível que 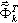 , ωk faça a aproximação de
, ωk faça a aproximação de 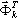 , Ω k com precisão arbitrária.
, Ω k com precisão arbitrária. - A abordagem proposta não é inferior ao método bem conhecido de decomposição modal (sobreposição). Ambos os métodos constituem casos particulares do método de projeção comum e convergem para a solução “exata” quando N -> Neq. (Essa declaração não é válida exatamente para o método de espectros de resposta, porque esse método é de caráter estatístico e sua convergência para a solução exata ocorre quando N -> ∞. É óbvio que quando N > Neq surge um conflito de cálculos devido ao fato de que o número de vetores de base não pode ultrapassar Neq. Portanto, é possível obter diferentes soluções para diferentes vetores de base quando N = Neq. Essa é uma particularidade do método de espectros de resposta. Para métodos diferentes do método de espectros de resposta, a convergência completa ocorre quando N = Neq. A convergência para o caso do método de espectros de resposta deve ser considerada apenas no sentido estatístico, porque esse método constitui uma abordagem estatística que visa obter uma solução média quando o histórico de tempo foi perdido. Em virtude disso, o termo “solução exata” deve ser aplicado com cautela).
- Qual é a melhor base: vetores Ritz ou vetores próprios? Deve existir uma base que garanta uma melhor convergência para a solução “exata” (N = Neq) através do menor número de funções de base N. A questão deve ser resolvida com a análise de exemplos práticos.
Normalmente, a primeira parte dos pares
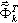 , ωk fornece boas aproximações para os pares próprios da correspondência
, ωk fornece boas aproximações para os pares próprios da correspondência 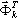 , Ω k (é possível determinar a precisão de cada par na coluna “Precisão” da listagem de saída). Somente a última parte dos pares
, Ω k (é possível determinar a precisão de cada par na coluna “Precisão” da listagem de saída). Somente a última parte dos pares 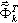 , ωk fornece aproximações incorretas para os pares próprios exatos e pode ser considerada como “pseudomodos” (do ponto de vista da norma sísmica francesa PS-92).
, ωk fornece aproximações incorretas para os pares próprios exatos e pode ser considerada como “pseudomodos” (do ponto de vista da norma sísmica francesa PS-92). - O uso do subespaço completo Q = {q1, q2, ..., qN} garante um rápido aumento da porcentagem de massa. No caso dos modos modal e sísmico, somente uma parte desse subespaço é usada.
Anexo 3C
Exemplos de aplicação dos modos sísmico e pseudomodo.
É evidente que existem muitos tipos de problemas sísmicos e espectrais nos quais é difícil obter uma percentagem suficiente (70% – 90%) de massas. É possível resolver os chamados problemas “bons” usando métodos conhecidos.
- Atribua um número arbitrário de modos N.
- Calcule os primeiros modos N sequenciais com o modo modal.
No entanto, para problemas difíceis, essa abordagem pode revelar-se impossível. Consideremos, por exemplo, os problemas Coreal ou do museu. São modelos FEM que foram preparados por engenheiros franceses. É apresentada uma porcentagem de massa para um número diferente de modos próprios definidos. É usado o modo modal (método Lanczos).
Histórico de convergência do problema Coreal
|
Número de modos convergidos |
Percentual de massa |
|---|---|
|
44 |
< 1% |
|
62 |
12% |
|
75 |
38% |
|
89 |
60% |
|
116 |
74% |
|
154 |
77% |
|
179 |
80% |
Histórico de convergência do problema do museu
|
Número de modos convergidos |
Percentual de massa |
|---|---|
|
41 |
20% |
|
106 |
40% |
|
119 |
42% |
Por exemplo, 80% significa que, para duas direções, as somas de massas não são menores do que o número especificado. O modo modal gera modos próprios, enquanto é alcançada a porcentagem de massa adotada ou é esgotado o número de modos de limite superior atribuídos. A solução final do método de espectros de resposta é obtida na forma de sobreposição estatística de vetores próprios.
Em ambos os problemas considerados, o número de graus de liberdade é inferior a 2.000. Tais problemas são considerados pequenos (com relação ao número de graus de liberdade). Nos casos de problemas de média e larga escala (difíceis), é possível que os modos modal e sísmico permaneçam inaplicáveis na prática devido ao caráter expansivo do processo de cálculo. Nesses casos, é recomendada a aplicação do pseudomodo. É apresentado abaixo o histórico de convergência dos problemas Coreal e do museu.
“Histórico de convergência” para o problema “Coreal”
|
Número de vetores de base |
Percentual de massa |
|---|---|
|
10 |
58% |
|
20 |
67% |
|
40 |
70% |
|
80 |
80% |
“Histórico de convergência” para o problema “Museu”
|
Número de vetores de base |
Percentual de massa |
|---|---|
|
10 |
60% |
|
20 |
66% |
|
40 |
71% |
A convergência dos resultados no pseudomodo é ilustrada no próximo problema. A tabela a seguir apresenta os valores máximos/mínimos resultantes da combinação CQC para os modos modal e pseudomodo.
|
Modo |
UX (cm) |
UY (cm) |
UZ (cm) |
Porcentagem de massa |
|---|---|---|---|---|
|
Modal |
5.52002e-00 |
5. 88293e-00 |
5.83013e-00 |
81% |
|
Pseudomodo, Nvect = 10 |
5.58710e-00 |
5. 89055e-00 |
5.00224e-00 |
80% |
|
Pseudomodo, Nvect = 20 |
5.52937e-00 |
5.88870e-00 |
6.08661e-00 |
91% |
Nvect – o número de vetores de base.
Anexo 3D
Aplicação de métodos de análise modal para a solução de problemas de larga escala
Exemplo 1
Comparação do tempo de cálculo para os métodos BLSI e Lanczos. São considerados diferentes números de modos próprios.
Solver aplicado: solver direto esparso. Tipo de matriz de massa: fragmentada com rotações.
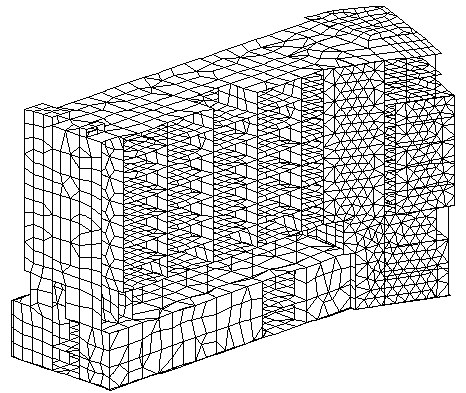
Fig. D1. Modelo de um hotel. Número de nós: 6.359; Número de elementos: 7.264; Número de equações: 37.806.
Tabela D1. Comparação de resultados
|
BLSI |
Lanczos |
||
|---|---|---|---|
|
f (Hz) |
Precisão |
F (Hz) |
Precisão |
|
2,794e-001 |
1,082e-006 |
2,794e-001 |
5,680e-015 |
|
1,388e+000 |
1,389e-004 |
1,388e+000 |
2,199e-013 |
|
1,520e+000 |
7,847e-004 |
1,520e+000 |
8,193e-012 |
|
1,644e+000 |
2,469e-004 |
1,644e+000 |
4,497e-013 |
|
1,747e+000 |
2,691e-004 |
1,747e+000 |
5,455e-014 |
|
1,776e+000 |
3,092e-004 |
1,776e+000 |
9,127e-013 |
|
1,806e+000 |
3,153e-004 |
1,806e+000 |
6,621e-013 |
|
1,818e+000 |
6,383e-004 |
1,818e+000 |
3,656e-012 |
|
2,622e+000 |
1,565e-003 |
2,343e+000 |
2,047e-011 |
|
2,634e+000 |
1,383e-003 |
2,622e+000 |
1,223e-005 |
Como a verificação de Sturm não é executada, o par próprio ignorado ocorre entre os modos 8º e 9º, quando o método BLSI é aplicado.
Tabela D2. Duração da extração do modo (em segundos)
|
Método |
10 modos |
50 modos |
100 modos |
|---|---|---|---|
|
BLSI |
735 |
6029 |
23572 |
|
Lanczos |
1472 |
12637 |
25271 |
Fatoração da matriz: 841 s.
Os métodos avançados (BLSI, Lanczos) baseados em um poderoso solver direto esparso produzem rapidamente a fatoração da matriz e extraem um grande número de modos próprios. Os cálculos foram executados em um computador P-350 (256 MB de RAM).
Exemplo 2
Aplicação de diferentes métodos para a solução do problema PJG203. O modelo contém vínculos rígidos que levam ao uso de uma matriz de massa consistente. Foram extraídos 25 pseudomodos.
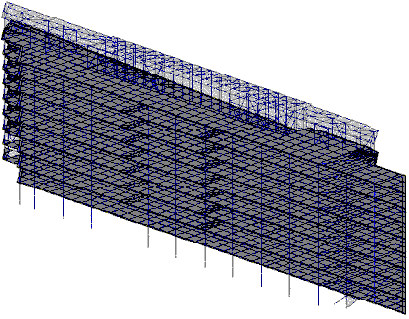
Fig. D2. Problema PJG203. Número de nós: 5.945; número de elementos: 11.471; número de vínculos rígidos: 22; número de nós compatíveis: 302; número de equações: 34.266.
Tabela D3. Tempo de cálculo, armazenamento em disco, as dez primeiras frequências e a precisão correspondente dos diferentes métodos.
|
Método |
Tempo (s) |
HDD (MB) |
Frequências (Hz) |
Precisão |
|---|---|---|---|---|
|
Linha do horizonte |
61 633 |
597 |
1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.829e+000 3.033e+000 3.209e+000 3.595e+000 |
8.043e-015 1.025e-013 1.031e-013 1.712e-006 5.566e-006 6.331e-008 3.538e-001 3.052e-005 9.086e-005 4.498e-003 |
|
Esparso |
4 435 |
99 |
1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.825e+000 3.033e+000 3.209e+000 3.595e+000 |
3.522e-012 2.689e-011 1.159e-010 1.735e-006 5.639e-006 6.419e-008 3.520e-001 3.034e-005 9.938e-005 4.386e-003 |
|
Lanczos modif. |
3 459 |
24 |
1.175e+000 1.337e+000 1.454e+000 2.445e+000 2.445e+000 2.628e+000 2.791e+000 3.033e+000 3.209e+000 3.595e+000 |
3.719e-004 3.891e-004 6.601e-004 1.454e-003 1.875e-003 2.946e-003 3.364e-003 3.923e-003 2.175e-002 1.580e-001 |
|
PCG_RITZ |
1 521 |
24 |
1.266e+000 1.350e+000 1.467e+000 2.445e+000 2.446e+000 2.446e+000 2.805e+000 3.035e+000 3.381e+000 3.566e+000 |
N/D – PCG_Ritz não é um método iterativo, é um método Ritz. Portanto, são obtidos os pseudomodos em vez dos modos próprios “exatos” |
Os seguintes parâmetros foram usados para o método Lanczos modificado: solver iterativo AEBEIS (modo multinível); pré-condicionamento ICCF; 2 níveis de agregação; 4 iterações internas, tol = 1.0e-04 – precisão de geração de vetores Lanczos.
Os seguintes parâmetros foram adotados para o método PCG_Ritz: solver iterativo AEBEIS multinível; pré-condicionamento ICCF; 1 nível de agregação; 4 iterações internas.
As frequências convergidas estão marcadas em vermelho. Se a precisão (consulte o Anexo 3A) de uma norma relativa de um vetor residual para um determinado modo for menor do que 5.0e-02, tal norma poderá ser considerada como totalmente convergida para o vetor próprio correspondente. Portanto, as frequências marcadas em vermelho são consideradas como os valores exatos para um determinado modelo discreto. A estimativa de erros do método PCG_Ritz é apresentada na tabela D4. Pode-se concluir que os resultados obtidos pelo método PCG_Ritz fornecem uma aproximação suficientemente boa para fins de engenharia e que tal abordagem pode ser usada para a estimativa rápida do comportamento sísmico.
Os métodos avançados permitem reduzir drasticamente o tempo de cálculo e os requisitos de armazenamento em disco sem nenhuma perda significativa em termos de exatidão.
Tabela D4. Estimativa de erros do método PCG_Ritz
|
Frequência “exata” |
Resultados do PCG_Ritz |
Erro (%) |
|---|---|---|
|
1.175e+000 |
1.266e+000 |
7.7 |
|
1.337e+000 |
1.350e+000 |
1.0 |
|
1.454e+000 |
1.467e+000 |
0.9 |
|
2.445e+000 |
2.445e+000 |
0.0 |
|
2.445e+000 |
2.446e+000 |
0.0 |
|
2.628e+000 |
2.446e+000 |
7.0 |
|
2.791e+000 |
2.805e+000 |
0.5 |
|
3.033e+000 |
3.035e+000 |
0.1 |
|
3.209e+000 |
3.381e+000 |
5.4 |
|
3.595e+000 |
3.566e+000 |
0.8 |
Os cálculos foram executados em um computador PC-450 (128 MB de RAM).
Exemplo 3
Foi considerada uma placa quadrada fina com uma matriz de massa consistente fixada ao longo de uma aresta. Foram usados o elemento de casca de 4 nós e a malha de 128x128 (número de equações Neq é 99.072). Os 40 pseudomodos foram extraídos.
O tempo de cálculo e o armazenamento de espaço em disco para os métodos Lanczos (horizontal e esparso), Lanczos modificado (solver iterativo) e gradiente Ritz (PCG_Ritz) são apresentados na tabela D5.
Tabela D5. Tempo de cálculo e requisitos de armazenamento em disco para diversos métodos.
|
Método |
Tempo (s) |
HDD (MB) |
|---|---|---|
|
Lanczos, solver de linha do horizonte |
141 559 |
7 367 |
|
Lanczos, solver esparso |
15 615 |
157 |
|
Lanczos modificado, solver iterativo |
18 978 |
0 – no núcleo |
|
PSG_Ritz |
9 651 |
192 |
Os cálculos foram executados em um computador PC-450 (128 MB de RAM).
As dez primeiras frequências obtidas pelo método Lanczos (linha do horizonte ou esparso) e Lanczos modificado (adotou-se: solver iterativo, pré-condicionamento ICCF, 3 níveis de agregação, 8 iterações internas, tolerância 1.0e-03 para geração de vetores Lanczos) são idênticas. Como a precisão dos cálculos era muito alta, foi possível considerar esses valores como exatos no âmbito do modelo discreto fornecido. Eles são adotados como valores Etalon para estimativa de erros para frequências obtidas pelo método PCG_Ritz. A abordagem multinível com pré-condicionamento ICCF (um nível de agregação, 4 iterações internas) foi selecionada quando o método PCG_Ritz estava sendo aplicado. Os resultados correspondentes são apresentados na tabela D6.
Tabela D6. Comparação de frequências dos métodos PCG_Ritz e Lanczos
|
Frequências do Lanczos (Hz) |
Precisão |
Frequências do PCG_Ritz (Hz) |
Erro (%) |
|---|---|---|---|
|
3.722e+000 |
5.918e-014 |
3.725e+000 |
0.08 |
|
9.112e+000 |
4.474e-014 |
9.115e+000 |
0.03 |
|
2.282e+001 |
2.424e-012 |
2.284e+001 |
0.09 |
|
2.915e+001 |
5.866e-013 |
2.915e+001 |
0.00 |
|
3.315e+001 |
1.795e-013 |
3.318e+001 |
0.09 |
|
5.801e+001 |
2.373e-011 |
5.803e+001 |
0.03 |
|
6.565e+001 |
3.028e-011 |
6.571e+001 |
0.09 |
|
6.873e+001 |
6.907e-014 |
6.875e+001 |
0.03 |
|
7.602e+001 |
1.549e-012 |
7.609e+001 |
0.09 |
|
9.949e+001 |
3.302e-013 |
9.953e+001 |
0.04 |
Exemplo 4
Um edifício grande é apresentado na Fig. D3
Fig. D3. Edifício grande. Número de nós: 26.126, número de elementos: 30.272,
número de equações: 15.5920.
São consideradas a análise estática linear (um caso de carga única) e a extração de 10 modos próprios. A tolerância adotada para o solver iterativo é igual a 1.0e-04. Para o solver de linha do horizonte, é usado o método Lanczos. Para o solver direto esparso, são aplicados os métodos Lanczos e BLSI. O método Lanczos modificado é usado para o solver iterativo (método de multinível com 3 níveis de agregação, 4 iterações internas, pré-condicionamento ICCF). Tipo de matriz de massa: fragmentada com rotações.
Tabela D7. Cálculo do tempo e do espaço em disco para diversos métodos
|
Método |
Espaço em disco (MB) |
Estática linear (rhs simples) (s) |
Extração de 10 modos próprios (s) |
Tempo total (s) |
|---|---|---|---|---|
|
Linha do horizonte |
5 702 |
136 065 |
65 052 |
203 878 |
|
AEBEIS |
52 |
2 442 |
25 793 |
28 355 |
|
Esparso (método Lanczos) |
773 |
10 253 |
24 500 |
35 762 |
|
NS esparso (método BLSI) |
773 |
10 253 |
11 534 |
22 604 |
Os cálculos foram executados em um computador PC-450 (128 MB de RAM).
Conclusões
Métodos avançados: BLSI e Lanczos com base em um solver direto esparso e um solver iterativo de alto desempenho AEBEIS com pré-condicionamento ICCF são ferramentas muito eficazes para a solução de problemas estáticos lineares de larga escala e de valor próprio. Eles reduzem consideravelmente o tempo de cálculo e os requisitos de armazenamento em disco em comparação com um solver de horizonte convencional. O método gradiente Ritz PCG_Ritz é uma abordagem rápida que permite estimar o comportamento sísmico de uma determinada estrutura. Quando um único nível de agregação é aceito, os resultados correspondentes, obtidos pelo método PCG_Ritz, são próximos dos obtidos pelos métodos Lanczos ou BLSI.
Referências
- E.L.Wilson. An eigensolution strategy for large systems. Computers&Structures, Vol. 16, Nº 1-4, pág. 259-265, 1983.
- Wilson. A new method of dynamic analysis for linear and nonlinear systems. Finite Elements in Analysis and Design, 1, 1985, 21-23, North-Holland.
- E.L.Wilson, Three dimensional dynamic analysis of structures, Computers and Structures, Inc., Berkeley, California, USA, 1996.
- R.W.Clough, J.Penzien. Dynamics of Structures. McGraw-Hill Book Comp., 1975, 634 pág.
- Fialko S. Yu. Investigations of the Initial Imperfections Influence to Natural Vibrations of Ribbed Conical Shells, Soviet Applied Mechanics, 1982, 18, N11, pág. 118-122. (em russo)
- Fialko S. Yu. Nonsteady vibrations of ribbed conical shells under the influence of local loads, Soviet Applied Mechanics, 1987, v23, N6, pág. 547-552.
- Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. pág. 193-207.
- Fialko S.Yu. High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis. CAMES (Computer assisted mechanics – engineering sciences), IV, 2000
- Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 – 60, 1988.
- Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 – 69, 1989.
- Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 – 207, 1987.
- Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
- S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, pág. 75-104.
- Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conferência sobre os efeitos do carregamento rápido e transitório no contexto de mecânica estrutural, Lausanne, Suíça, 26 e 27 de agosto de 1987.
- Hughes T.J.R., R.M.Ferencz, and j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61
- Hughes Th. J. R. “The Finite Element Method. Linear Static and Dynamic. FEM Analysis”.
- Parlett B.N., 1980. “The Symmetric Eigenvalue Problem”. Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632.
- Bulgakov, V.E., Belyi, M.E., Mathisen, K.M. Multilevel aggregation method for solving large-scale generalized eigenvalue problems in structural dynamics, Int. j. Numer. Methods Eng., 40: 453 – 471, 1997.
- Bulgakov, V.E. Iterative aggregation technique for large-scale finite element analysis of mechanical systems, Comput. Struct, 52: N4, 829-840, 1994.
- Bulgakov, V.E., G. Kuhn. High-performance multilevel iterative aggregation solver for large finite-element structural analysis problems, Int. j. Numer. Methods Eng., 38: 3529-3544, 1995.
- Guia normativo
- I.Ja.Amiro, V.A.Zarucky, V.N.Revutsky, Yu.V.Skosarenko, A.I.Telalov, S.Yu.Fialko. Oscillations of Ribbed Shells of Revolution, Kiev, Naukova Dumka, 1988, pág. 169 (em russo).
- S.Yu.Filako. Natural Vibration Modes of Ribbed Conical Shells, Soviet Applied Mechanics, 1984, v20, N11, pág. 1033-1037. (em inglês)