Определения переходной кривой

По отношению к другим прямым участкам и кривым каждая переходная кривая может быть входящей или исходящей.

При проектировании и разметке переходных кривых часто используются такие параметры как L (длина переходной кривой) и R. Параметр R обозначает радиус кривизны на одном конце переходной кривой. Чтобы различать радиусы в начале и конце переходной кривой, можно использовать значения R₁ и R₂.

На следующей иллюстрации показаны различные параметры переходной кривой:

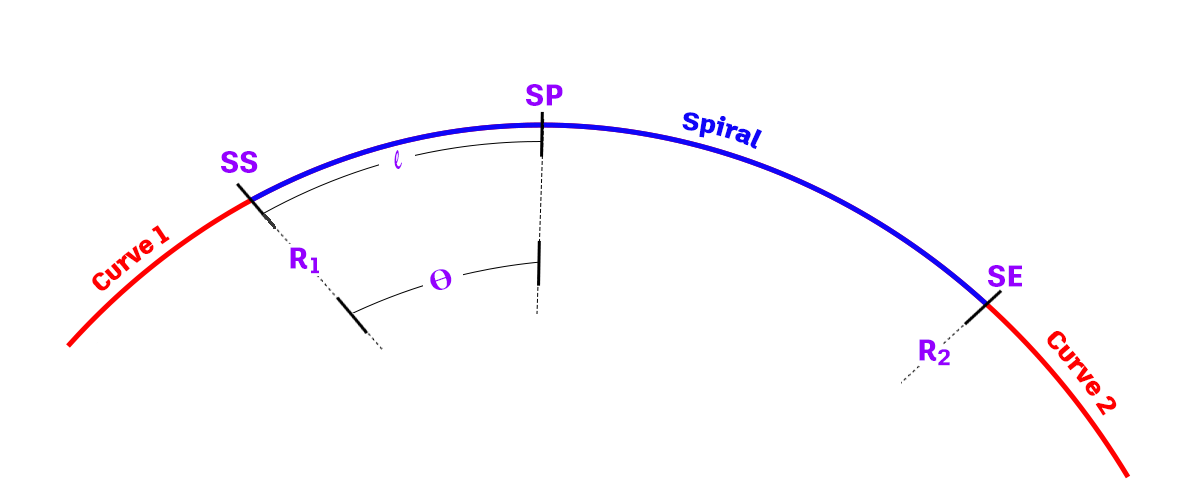
Параметр переходной кривой	Описание
R₁	Радиус кривой 1.
R₂	Радиус кривой 2.
ПП	Начальная точка переходной кривой.
SE	Конечная точка переходной кривой.
SP	Точка переходной кривой на расстоянии длины дуги l.
Θ	Центральный угол в точке переходной кривой на расстоянии длины дуги l.
l	Длина дуги от начальной точки переходной кривой вдоль кривой.
L	Общая длина дуги переходной кривой между начальной и конечной точками переходной кривой.

Составная переходная кривая

Составные переходные кривые служат для создания перехода между двумя круговыми кривыми различного радиуса. Существует два типа переходной кривой: простая и составная. Составная переходная кривая включает кривую, состоящую в свою очередь из двух простых переходных кривых. В ней есть два пролета, каждый из которых представляет собой простую переходную кривую, непрерывно соединяющуюся по касательной со смежной переходной кривой. Они обеспечивают непрерывность функции кривизны и представляют собой метод создания плавного перехода в вираже.

Клотоида (переходная кривая)

В Autodesk Civil 3D поддерживается использование нескольких типов переходных кривых, однако наиболее часто используются переходные кривые типа «клотоида». Переходная кривая типа "клотоида" используется в проектировании автомобильных и железных дорог инженерами во всем мире.

Функция кривизны клотоиды, впервые исследованная швейцарским математиком Леонардом Эйлером, представляет собой линейную функцию, выбранную таким образом, что в месте соединения переходной кривой с прямолинейным участком кривизна как функция длины равна нулю. Далее кривизна возрастает линейно до тех пор, пока не достигнет кривизны прилегающей кривой в точке соединения переходной кривой и кривой.

В отличие от простой кривой здесь также обеспечивается непрерывность местной кривизны, значение которой повышается для транспортных средств при высоких скоростях.

Формула

Клотоидные переходные кривые могут быть выражены в следующих формулах:

Где:

Θ = центральный угол в точке переходной кривой на расстоянии длины дуги l.
l = длина дуги вдоль кривой.

См. приведенную выше схему для справки.

Пологость переходной кривой:

Общий угол, стягиваемый переходной кривой:

Длина касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой.

Расстояние смещения касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой:

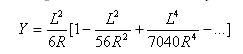
Переходная кривая Блосса

Вместо клотоиды на переходе можно использовать переходную кривую Блосса. Преимущество этой переходной кривой в сравнении с клотоидой заключается в том, что сдвиг P здесь меньше, поэтому переход получается более длинным, как и выступ переходной кривой (K). Этот фактор имеет важное значение при проектировании рельсовых путей.

Формула

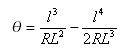
Переходные кривые Блосса можно выразить как:

Другие распространенные выражения

Длина касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой.

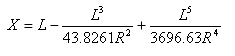
Расстояние смещения касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой:

Синусоидальные кривые

Эти кривые характеризуются согласованным дирекционным углом кривизны; они применяются для перехода между прямыми участками с отклонением 0 и 90 градусов. Однако синусоидальные кривые не имеют широкого применения, так как они более пологи, чем истинная спираль, из-за чего их труднее представлять в табличной форме и размечать.

Формула

Синусоидальные кривые могут быть представлены в виде следующего выражения:

Где:

Θ = центральный угол в точке переходной кривой на расстоянии длины дуги l.
l = длина дуги вдоль кривой.

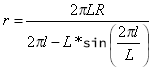
См. приведенную выше схему для справки.

Где r — радиус кривизны в любой заданной точке.

Убывающая половина синусоиды с прямым участком

Уравнение такой формы часто используется в проектировании железных дорог в Японии. Применение этой кривой целесообразно в ситуациях, при которых требуется эффективно изменить кривизну при малых (с точки зрения динамических характеристик транспортного средства) углах отклонения.

Формула

Кривые типа "убывающая половина синусоиды с прямым участком" можно выразить как:

Где и X — это расстояние от начальной точки до любой точки кривой, измеряемое вдоль (удлиненного) начального прямого участка; X — общее значение Х в конце кривой перехода.

Другие распространенные выражения

Длина касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой.

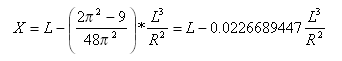
Расстояние смещения касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой:

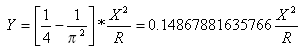
Кубические параболы

Кубические параболы сходятся не так быстро, как кубические переходные кривые, что делает их весьма востребованными при проектировании железных дорог и автострад.

Формула

Минимальный радиус кубической параболы

Радиус в любой точке кубической параболы:

Где Θ = центральный угол в точке переходной кривой на расстоянии длины дуги .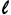

См. приведенную выше схему для справки.

Кубическая парабола достигает минимального значения r при:

Поэтому

Радиус кубической параболы убывает от бесконечности до значения при 24 градусах, 5 минутах 41 секунде, а затем начинает возрастать снова. Это делает кубические параболы бесполезными при отклонениях, превышающих 24 градуса.

Кубическая кривая (JP)

Этот переход был разработан в соответствии с требованиями, действующими в Японии. Для ситуаций, в которых требуется применить малый угол отклонения или большой радиус, разработано несколько аппроксимаций клотоиды. Одной из таких аппроксимаций, используемой при проектировании в Японии, является кубическая кривая (JP).

Формула

Кубические кривые могут быть выражены как:

Где Х = длина касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой.

Эту формулу можно также выразить следующим образом:

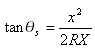
Где обозначает центральный угол переходной кривой (показанный как i1 и i2 на изображении).

Другие распространенные выражения

Длина касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой.

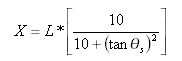
Расстояние смещения касательной, выходящей из точки соединения прямого участка и переходной кривой, измеренная в точке соединения переходной кривой и кривой:

Кубическая парабола NSW

Это тип кубической параболы, измененной в соответствии с требованиями штата Новый Южный Уэльс.

Формула

Кубическую параболу NSW можно выразить в следующем виде:

Где:

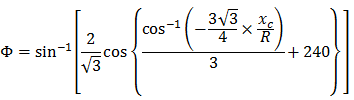
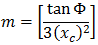
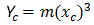
Φ = угол между конечной радиальной линией в R и линией, перпендикулярной исходному прямому участку
R = радиус кривой
X_c = общее значение X для заданной переходной кривой
Y_c = общее значение Y для заданной переходной кривой

Би-квадратичные переходные кривые (Шрамма)

Для би-квадратичных переходных кривых (Шрамма) характерны низкие значения вертикального ускорения. Они состоят из двух парабол второй степени, радиусы которых изменяются как функция длины кривой (l).

Формула простой кривой

Кривизна первой параболы:

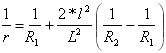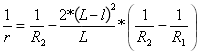при