Передаваемый крутящий момент

Где:

	P	передаваемая мощность [фунт/фут]
	n	скорость [мин–1]

Минимальный диаметр вала

1. Внутренний диаметр вала dh > 0

a)

б) если dmin ≤ dh -> dmin = 1,1 dh [д]

В противном случае для поиска оптимального диаметра используется следующая формула:

2. Внутренний диаметр вала dh = 0

Где:

	dmin	минимальный диаметр вала [д]
	dh	внутренний диаметр вала [д]
	T	крутящий момент [фунт/фут]
	Ka	коэффициент внешней динамической нагрузки
	Kf	коэффициент усталостной долговечности
	Sv	необходимый запас прочности
	τAl	допустимое напряжение среза

Общий расчет

Минимальная длина шлица для передачи крутящего момента

1. Фиксированное соединение:

2. Гибкое соединение:

Где:

	T	крутящий момент [фунт/фут]
	Ka	коэффициент внешней динамической нагрузки
	Kf	коэффициент срока службы до полного износа
	Kw	коэффициент внешней динамической нагрузки
	Km	коэффициент распределения нагрузки
	Sv	необходимый запас прочности
	ds	средний диаметр = (D + d) / 2 [д]
	D	наружный диаметр участка с пазом [д]
	d	внутренний диаметр участка с пазом [д]
	N	количество канавок [–]
	h	высота канавки = (D – d) / 2 [д]
	s	фаска [д]
	hst	высота соединения hst = h – 2s [д]
	pDmin	допустимое давление на опорной поверхности вала или канавки [фунт/кв. дюйм]

Допустимое давление

1. Фиксированное соединение:
2. Гибкое соединение:
Где:

	T	крутящий момент [фунт/фут]
	Ka	коэффициент внешней динамической нагрузки
	Kf	коэффициент срока службы до полного износа
	Kw	коэффициент внешней динамической нагрузки
	Km	коэффициент распределения нагрузки
	Sv	необходимый запас прочности
	ds	средний диаметр = (D + d) / 2 [д]
	D	наружный диаметр участка с пазом [д]
	d	внутренний диаметр участка с пазом [д]
	N	количество канавок [–]
	h	высота канавки = (D – d) / 2 [д]
	s	фаска [мм]
	hst	высота соединения hst = h – 2s [д]
	lf	активная длина шпонки [д]

Проверка прочности

pmin ≤ pDs

pmin ≤ pDh

Где:

	pmin	минимальное расчетное давление h/2 [фунт/кв. дюйм]
	pDs	допустимое давление в вале [фунт/кв. дюйм]
	pDh	допустимое давление в ступице [фунт/кв. дюйм]

Напряжение сдвига в основании наружных шлицев

Для передаваемого крутящего момента T напряжение сдвига при кручении, наведенное на валу в основании наружных шлицев

Для цельного вала

Для полого вала

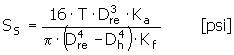
Напряжение сдвига на делительной окружности

Напряжение сдвига от переданного крутящего момента T на делительной окружности шлицев

Расчетная длина шлица:

Lf = min {L, Le} [д]

Сжимающие напряжения по сторонам шлица

Для шлицевых участков допустимые сжимающие напряжения всегда намного меньше аналогичных величин для зубчатых колес. Причина этого заключается в неравномерности распределения нагрузок, что приводит к варьированию рабочих режимов в разных местах шлица.

Для подвижных шлицев

Для фиксированных шлицев

Где:

Расчетная длина шлица	Lf = min {L, Le} [д]
Глубина зацепления шлица h h ≅ 0,9 / P [д]	для шлицев с плоской выемкой
h ≅ 1 / P [д]	для шлицев со скругленной выемкой

Разрушающие напряжения на шлицах

Внутренние шлицы могут подвергаться разрушению из-за растягивающих напряжений от радиального компонента переданной нагрузки, центробежных и тангенциальных усилий на делительной окружности, вызывающих изгиб шлица.

1. Напряжение при растяжении с радиальной нагрузкой

Где: толщина стенки внутреннего шлица	tw = Doi – Dri [д]
2. Центробежное напряжение при растяжении
3. Напряжения при растяжении с нагрузкой на балку

Где: расчетная длина шлица

Lf = min {L, Le} [д]

4. Суммарное напряжение разрыва с тенденцией к разрушению края внешнего шлица

Выпуклые шлицы (для больших взаимных смещений)

Выпуклые шлицы могут работать в условиях угловых смещений до примерно 5 градусов. Нагрузочная способность выпуклых шлицев при точной юстировке намного меньше, чем у прямых, но они проявляют себя с лучшей стороны в условиях больших смещений.

В американском стандарте описаны формы выпуклых наружных шлицев, которые могут совмещаться со внутренними шлицами стандартной формы.

Сжимающее напряжение на шлице

Где:

Радиус кривизны выпуклого шлица	r2 ≅ F2 / 8A [д]
Радиус скругления	r1 = r2 tan Φ [д]
Глубина зацепления шлица h h ≅ 0,9 / P [д]	для шлицев с плоской выемкой
h ≅ 1 / P [д]	для шлицев со скругленной выемкой

Используемые переменные

T	крутящий момент [фунт/фут]
n	скорость [мин–1]
D	диаметр делительной окружности [д]
Dri	диаметр окружности впадин внутреннего шлица [д]
Dre	диаметр окружности впадин внешнего шлица [д]
Dh	внутренний диаметр полого вала [д]
Doi	наружный диаметр втулки с пазами [д]
N	количество канавок [–]
h	высота канавки [д]
Lf	расчетная длина шлица [д]
L	рабочая длина шлица [д]
Le	максимальная эффективная длина [д]
t	действительная толщина шлица, по окружности [д]
tw	толщина стенки внутреннего шлица = половина разности наружного диаметра втулки шлица и диаметра окружности выступов [д]
Φ	угол хода [град]
Y	Коэффициент Льюиса для конфигурации шлицев. В расчете используется значение Y = 1,5.
F	угол зубчатого зацепления [град]
Sv	необходимый запас прочности
A	выступ скругления на концах шлица [д]
r1	радиус сопряжения выпуклого шлица [д]
r2	радиус кривизны скругленного зуба для выпуклого шлица [д]
Ka	коэффициент внешней динамической нагрузки
Kf	коэффициент срока службы до полного износа
Kw	коэффициент внешней динамической нагрузки
Km	коэффициент распределения нагрузки
Ks	коэффициент бокового контакта шлицев
	Ks = 0,5 для шлицев с обычной и повышенной точностью установки (нагрузку принимает только половина шлица)
	Ks = 0,3 для шлицев с низкой точностью изготовления и установки (нагрузку принимает только одна треть шлица)