运动仿真 02
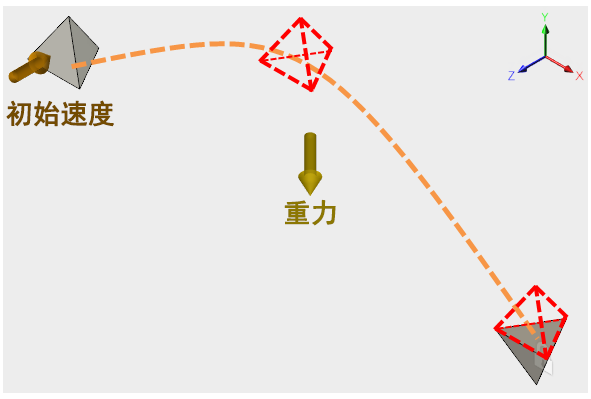
抛射体的抛物线轨迹。
案例描述
该精度验证示例论证了在量化以下三种现象时运动仿真求解器的可靠性:
- 初始线性速度
- 大自由体位移(运动动力学)
- 重力加速度和减速度
该模型是两个单元素四面体 — 一个可移动(供抛射),一个固定(静止)。该静止实体也称为刚体,它不会有任何变形。此外,这两个实体不会彼此交互(无接触)。静止实体仅用作一个位置参考。特别是,在运动仿真结束时,静止实体所在的位置使其顶面与抛射体底面的理论位置完全相对应。
作为初始条件,向此抛射体应用了两个相等的线性速度分量,一个垂直,一个水平。换句话说,生成的初始速度与水平方向向上成 45° 角。在理论上,对于给定的任意初始速度(忽略风阻力),此角度均会导致抛射体实现最大的水平行进距离。以下结果是确定的理论结果,并与 Fusion 运动仿真结果进行了比较:
- 当抛射体的垂直速度达到零并反向时它的高度(沿抛射体路径的最大高度)
- 达到抛射体的最大高度所需的时间
- 抛射体返回到其初始标高(返回到地面)所需的时间
- 当抛射体再次达到其初始标高时所穿过的水平距离
分析类型和参数
- 运动仿真
- 事件总持续时间 = 0.2 秒
- 结果保存间隔数 = 20(每 10 毫秒生成一个结果集)
- 单元删除标准:未设置
刚体
- 固定实体是刚性的
模型几何图元
- 说明:两个相同的四面体,所有边长度 = 0.866 英寸,所有面角角度 = 60°
- 静止实体位于与抛射体的初始位置之间的水平距离为 7.722 英寸的位置处。此外,静止实体已旋转,以便在运动仿真结束时它的顶面与抛射体底面的理论位置相对应。
网格参数
- 网格类型 = 实体,四面体
- 元素顺序 = 抛物线型
- 网格大小 = 1.0 英寸,绝对(导致每个零件一个元素,从而最大程度地增加允许的计算时间步并最大限度地减少求解时间)
- 自适应网格优化:无
材料特性
材料特性不影响抛射体运动的物理属性。但是,在运动仿真过程中,较高密度的零件比较低密度的零件求解速度更快。因此,选择了材料铅,它具有相对较高的密度。
- 弹性模量 = 2.031 X 106 psi
- 密度 = 0.4097 lbmass/in3
- 泊松比 (v) = 0.43
约束
- 静止实体被完全固定
载荷
重力:在 –Y 方向上,加速度 = 32.174 ft/sec2
初始线性速度:
在 X 方向上:3.2174 ft/s
在 Y 方向上:3.2174 ft/s
注意:您必须将默认“普通精度”设置从 0.123 更改为 0.1234,才能看到初始速度分量的第四个小数位。可以在“首选项”对话框的“单位和值显示”部分中找到此设置。
理论结果
垂直速度达到零所需的时间
时间1 = 初始速度(垂直分量)/减速率
`时间1 = (3.2174 ft/s) / (32.174 ft/s2) = 0.1 s(与运动仿真的步 10 相对应)
抛射体返回到初始标高的时间
从最大高度返回到初始高度所需的时间等于从初始位置到达最大高度所需的时间。因此:
时间2 = 2 * 时间1
时间2 = 2 * 0.1 s = 0.2 s(与运动仿真的步 20 相对应)
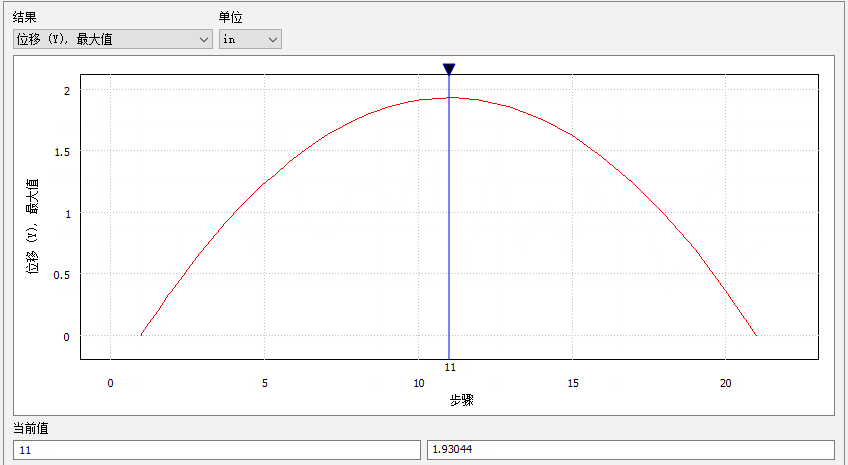
抛射体相对于初始位置所达到的最大高度(Y 位移)
最大高度 = 平均 Y 速度 * 时间1
平均 Y 速度 (in/s) = (12 in/ft) * 初始 Y 速度 (ft/s) / 2 = (12 in/ft) * (3.2174 ft/s) / 2 = 19.3044 in/s
最大高度 = 19.3044 in * 0.1 s = 1.93044 in
在运动结束时抛射体穿过的水平距离
在不考虑风阻力或任何其他反作用力的情况下,水平速度分量保持恒定。因此:
水平距离 (in) = (12 in/ft) \* 初始 X 速度 (ft/s) \* 时间2 = (12 in/ft) \* (3.2174 ft/s) \* 0.2 s = 7.72166 in
结果比较
增加图例的精度以将结果与具有更多小数位的理论结果进行比较。特别是,可以访问“首选项”对话框的“单位和值显示”部分。将“常规精度设置”从 1.123 更改为 1.12345。在“单位和值显示”>“仿真和衍生式设计”中,将“科学记数法的精度”设置从 1.123E+04 更改为 1.12345E+04。然后,对于小数结果,图例将显示五个小数位,对于科学记数法结果,也类似。
| 结果 | 理论 | Fusion | 差异 |
|---|---|---|---|
| 时间1 (当实现最大 Y 位移时) |
0.1 s | 0.1 s | 0 % |
| 最大 Y 位移 | 1.93044 in | 1.93044 in | 0 % |
| 时间2 (当抛射体返回到初始标高时) |
0.2 s (与步 20 相对应) |
0.2 s (与步 20 相对应) |
0 % |
| 在时间2时的 Y 位移 | 0 in | -3.30358 x 10-5 in | -3.30358 x 10-5 in |
| 在时间2时的 X 位移 | 7.72166 in | 7.72179 in | 0.0017% |
参考
从许多参考资料中都能找到基本牛顿物理学知识(运动方程)。