运动仿真 01
具有内部压力的厚空心球体的塑性变形。
案例描述
该精度验证示例论证了在量化以下三种现象时运动仿真求解器的可靠性:
- 时间相关的应用载荷
- 非线性材料行为,特别是当应用的载荷超出屈服时发生的塑性变形
- 使用对称,通过一部分更小的表达来确定完整实体的行为
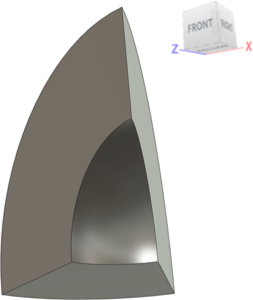
该模型是厚壁空心球体的十六分之一对称表达。对内腔表面应用了均匀压力。压力大小线性增加。在事件中的某点处,塑性变形在内部表面开始发生。随着运动仿真的继续,更多的壁厚逐渐达到塑性应力级别。最终,外部表面达到屈服应力,此时球体开始快速膨胀。此页面上显示了在内部表面和外部表面达到塑性状态所需的压力推导。Fusion 结果与理论结果进行比较。
假设使用了完全塑性的材料,这表示当屈服发生时,应力-应变曲线的斜率是平坦的(零)。换句话说,不存在材料的加工硬化。该假设可使理论推导变得更简单。
无摩擦约束表示在空心球体的每个切片(扁平)表面处的对称条件。
分析类型和参数
- 运动仿真
- 事件总持续时间 = 0.051 秒
- 结果保存间隔数 = 51(每毫秒生成一个结果集)
- 单元删除标准:未设置
模型几何图元
- 说明:空心球体的十六分之一(空心半球体的八分之一或 45° 段)
- 球体的内径 = 2 英寸
- 球体的外径 = 4 英寸
- 壁厚 = 2 英寸
网格参数
- 网格类型 = 实体,四面体
- 元素顺序 = 抛物线型
- 网格大小 = 0.333 英寸,绝对
- 自适应网格优化:无
材料特性
- 弹性模量 = 3.0 X 107 psi
- 密度 = 0.284 lbmass/in3
- 泊松比 (v) = 0.29
- 屈服强度 = 36,000 psi
- 非线性类型 = 塑性
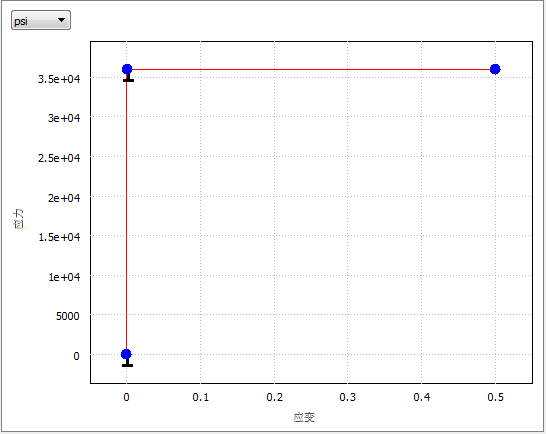
- 应力-应变数据:
| 应变 | 应力 – psi (kPa) |
|---|---|
| 0.0 | 0.0 |
| 0.0012 | 36,000 (248,211) |
| 0.5 | 36,000 (248,211) |
约束
- 三个平表面中每个平表面处的无摩擦结构约束
载荷
- 应用于内部球体表面的瞬态压力
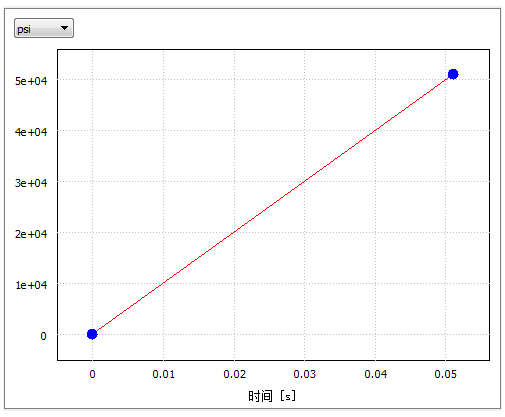
- 增强曲线数据(每毫秒压力增加 1,000 psi):
| 时间 | 大小 |
|---|---|
| 0.0 | 0.0 |
| 0.051 | 51,000 |
理论结果
随着塑性从内表面逐渐进展到外表面,我们来考虑适用于这两种极限情况的解决方案:
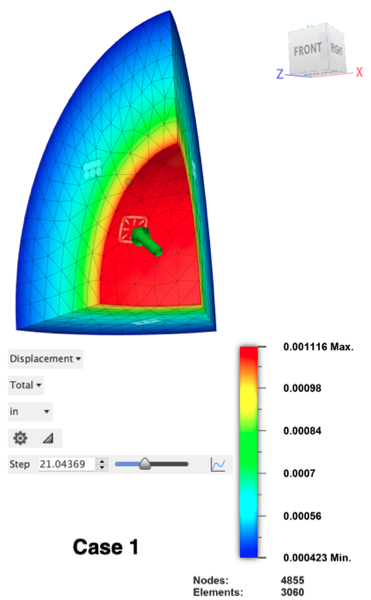
- 情况 1(塑性开始):内表面变得具有塑性
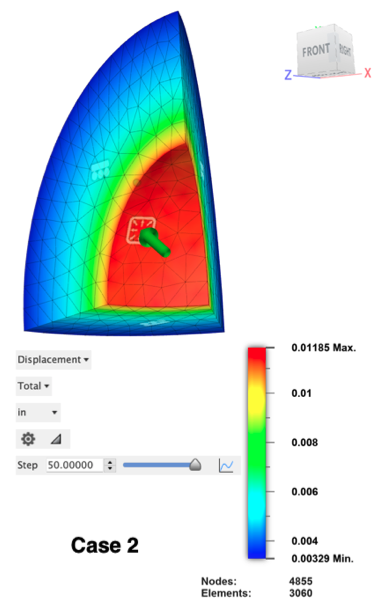
- 情况 2(100% 塑料穿透):外表面变得具有塑性
我们来计算两个变量 — 内表面的径向位移 (δi)(以英寸为单位)和应用压力 (P)(以 psi 为单位)。
情况 1(刚刚具有塑性)
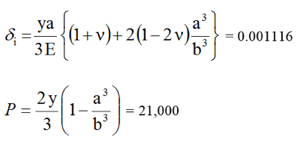
情况 2(100% 塑性)
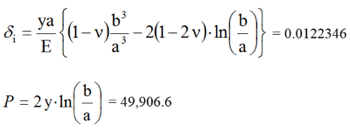
其中:
- y = 36,000 psi(材料的屈服应力)
- E = 30 x 106 psi(杨氏模量)
- ν = 0.29(泊松比)
- a = 2 in(球体的内径)
- b = 4 in(球体的外径)
结果比较
Fusion 会将结果内插在求解器的输出增量之间。使用最大 Mises 等效应力结果的二维图表可以确定模型刚刚达到 36,000 psi 应力级别时的应力。尽可能地找到图表上应力级别首先达到 36,000 psi 的点。将十字光标拖到图表上方时,进行放大以获得更好的分辨率。若要进行缩放,请单击并将光标拖动到图表的关键部分。情况 1 的步近似为 21.04。压力每步增加 1,000 psi。因此,情况 1 的应用压力为 21.04 * 1,000 psi = 21,040 psi。
显示相同步的总位移结果。由于球体的几何形状,所有位移均是径向的,并且在整个事件中最大位移出现在内表面上。
通过查看最大总位移结果的二维图表可以确定达到完全塑性时的压力。确定最大位移即将快速增加时的步。(一旦达到完全塑性,没有什么能阻止球体快速膨胀。) 大约在步 50.00 处,会发生这种情况。位移会逐渐增加到该步。从步 50.0001 开始,变化率显著增加。因此,情况 2 的应用压力为 50 * 1,000 psi = 50,000 psi,图例显示了相应的位移。
| 情况编号 | 应用压力 (psi): | 径向位移(英寸): | ||||
|---|---|---|---|---|---|---|
| 理论 | Fusion | 差异百分比 | 理论 | Fusion | 差异百分比 | |
| 1 | 21,000 | 21,040 | 0.19 % | 0.001116 | 0.001116 | -0.00 % |
| 2 | 49,906.6 | 50,000 | 0.19 % | 0.0122346 | 0.01185 | -3.14 % |
Reference
Chakrabarty, J.,塑性理论,McGraw-Hill,纽约,1987 年,第 307-311 页。