超弹性材料理论

诸如橡胶等超弹性材料的非线性应力-应变特性很复杂。许多可用等级的材料在行为上大不相同。对于 Fusion 中的非线性仿真，将使用 2 阶常数标准 Mooney-Rivlin 材料模型来表示超弹性材料。材料系数是根据曲线拟合通过实验获得的原始应力-应变数据得到的。此数据可能基于各种测试，包括以下拉伸/压缩测试示例：

• 单轴（1 和 2）
• 平面运动
• 等双轴
• 双轴
• 限制
• 三轴
• 体积

有关这些测试以及它们生成的原始数据的说明不在本主题的讨论范围之内。材料测试由专门研究工艺的实验室执行，且曲线拟合必须在 Fusion 以外的程序中进行。（该程序不具有内置的功能来接受原始数据并执行曲线拟合函数。）在获取原始数据后，有多种程序可用于执行必要的曲线拟合函数。其中一个程序是 HyperFit，该程序提供了免费软件演示版（功能有限）和许可版。需要具有完整许可才能生成曲线和结果材料常数。

Mooney-Rivlin 超弹性材料模型

使用 2 阶常数标准 Mooney-Rivlin 材料模型对 Fusion 中的超弹性材料进行建模。将使用几乎不可压缩行为公式，因此在应变能量函数中将包含体积项。将分开呈现剪切变形和体积变形的效应。

常规 Mooney-Rivlin 应变能量函数：

在以下常规函数中表示了应变能量、剪切变形和体积变形之间的关系（适用于 2 阶和更高阶的情况）：

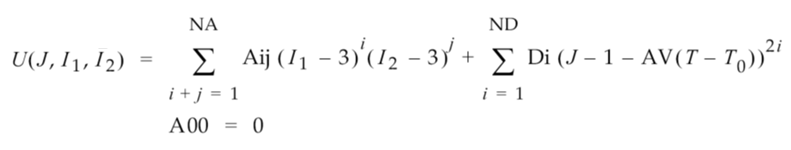
其中：

• U 是应变能量。
• I1 是第一个扭曲应变不变量。
• I2 是第二个扭曲应变不变量。
• J = det F，用于确定变形梯度。
• Aij 是与剪切变形相关的材料常数集（i 和 j 是各个常数的下标）。
• Di 是与体积变形相关的材料常数集。
• AV 是热膨胀的体积系数。
• T 是当前温度
• T0 是初始温度

简化的 2 阶常数 Mooney-Rivlin 方程式

目前，Fusion 在非线性分析中不支持超弹性材料的热效应。因此，我们可以通过消除热膨胀项（AV、T 和 T0）并算出 Fusion 接受的常数（A01、A10 和 D1）的总和，来简化前面的函数。那么，简化的应变能量方程式将如下所示：

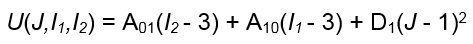
其中：

• U、J、I1** 和 I2 如前面所定义。
• A01 是与材料的剪切变形相关的两个扭曲常数中的第一个常数。
• A10 是与材料的剪切变形相关的两个扭曲常数中的第二个常数。
• D1 是与材料的体积变形相关的常数，等于体积模量 (K) 的一半。

即，2D1 = K。因此，D1 = K/2