热应力 02：准刚性连杆和两个桁架

确定当一个杆件的温度上升时产生的热应力。

案例描述

一个准刚性连杆绕其右端的孔转动。该连杆位于圆柱形黄铜杆的上面。一个圆柱形钢杆向下锚定在该连杆的左端。黄铜杆的温度从 20°C（部件的无应力温度）上升到 50°C。导致的热膨胀致使在钢压杆中产生拉伸应力。由于黄铜杆无法无限制地膨胀，因此在其中产生轴向压应力。我们会将此轴向应力与理论解进行比较。

在此主题分析类型中，刚性元素不可用。因此，通过使该连杆相对较大并将材料刚度设置为最大支持值来实现准刚性行为。在下图中，所有尺寸均以毫米为单位。

热应力图

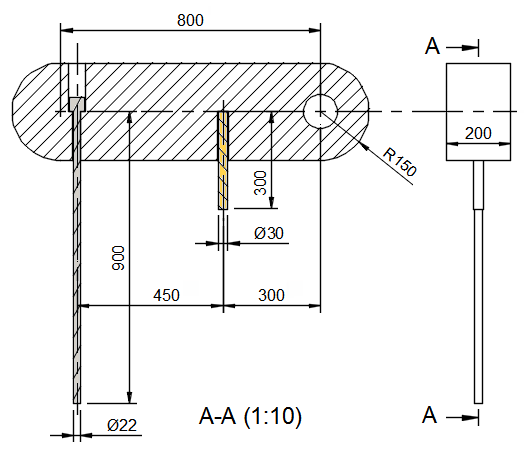
尺寸 (mm)

连杆：1100 x 300 x 200 总尺寸
黄铜杆：30 直径 x 300 长
钢杆：22 直径 x 900 长（不包括头）

分析类型和参数

分析类型：热应力
无应力参考温度：20°C

网格参数

网格类型 = 实体，四面体
网格大小 = 30 mm，绝对
元素顺序 = 抛物线型
自适应网格优化：无
局部网格控制：
- 连杆中的枢轴孔：15 mm 网格大小
- 钢杆和连杆中的关联孔面：5 mm 网格大小
- 黄铜杆和连杆中的关联孔面：7 mm 网格大小

材料特性

特性	链接	黄铜杆	钢杆
弹性模量 (MPa)	1.3 x 10⁶	105,000	200,000
泊松比	0.3	0.31	0.3
热膨胀系数 (/°C)	1.2 x 10^-5	1.88 x 10^-5	1.2 x 10^-5

注意：钢杆和连杆的热膨胀系数真的不重要，因为这两个零件不会遇到温度变化。

约束

连杆中的枢轴孔：销约束（径向和轴向方向）
钢杆的底端：固定
黄铜杆的底端：仅 Y 约束
黄铜杆的圆柱面：销约束（仅切向方向）

注意：此约束可防止该杆绕任何轴旋转，但允许它因热膨胀而在径向方向上增大。因此，该杆处于静态稳定状态，并且约束方案不会引起人工热应力。

热载荷

连杆和钢杆（每个杆的整个实体）：应用温度为 20°C
黄铜杆（整个实体）：应用温度为 50°C

接触参数

连杆中用于连接这两个杆的孔已确定间隙尺寸。因此，接触仅出现在两个位置：

在黄铜杆的顶端和连杆中关联盲孔的末端之间。
在钢杆头的底部和连杆中关联沉头孔的底部之间。

这两个接触集合的设置如下所示：

接触类型：分离
穿透类型：对称
热传导：1 x 10-6 W / (m2·K)

注意：所有三个实体获得应用温度，从而使黄铜杆变热，以确保其他两个零件的温度保持在无应力值。为了最大程度地减少零件接合处的热流量，要求热传导为零。但是，零传导值会导致求解失败。因此，我们指定无穷小的传导值。

理论解

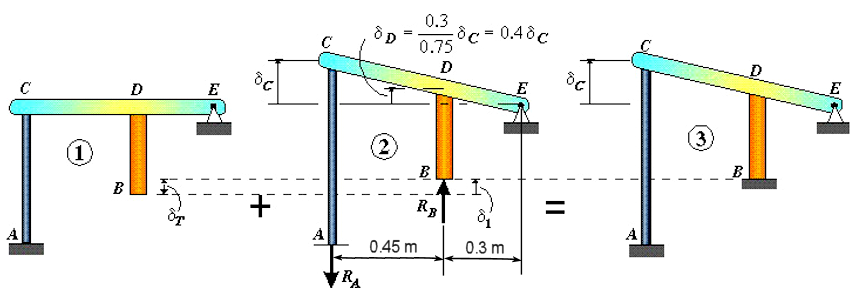
热应力理论图

考虑前面的图表，我们根据 Beer 和 Johnston 参考得出以下关系：

ΣME = 0 RA * (0.75 m) - RB * (0.3 m) = 0 RA = 0.4 RB

变形

使用了叠加方法。移除 RB 后，圆柱体温度上升导致点 B 向下移动距离 δT。反作用 RB 导致与 δT 相同大小的位移 δ1，从而使点 B 的最终变形为零。

根据以下方程式，由于温度上升 30°C (50°C - 20°C)，黄铜杆的长度（当不受约束时）增加 δT：

δT = L(ΔT)α = (0.3 m)(30° C)(1.88 x 10-5/° C) = 0.0001692 m

我们注意到 δD = 0.4 δC 且 δ1 = δD + δB-D，其中 δB-D 是黄铜杆的长度变化。

δC = RAL / (AE)

假设，对于钢杆，L = 0.9 m，A = πD2/4，D = 0.03 m 且 E = 105 x 109 Pa：

δC = 4 RA(0.9 m) / [π(0.03 m)2(105 x 109 Pa)] = 11.83797097 x 10-9 RA δD = 0.4 δC = 0.4 (11.83797097 x 10-9 RA) = 4.73518839 x 10-9 RA δB-D = RBL / (AE)

假设，对于黄铜杆，L = 0.3 m，A = πD2/4，D = 0.022 m 且 E = 105 x 109 Pa：

δB-D = 4 RB(0.9 m) / [π(0.03 m)2(105 x 109 Pa)] = 4.04203030 x 10-9 RB

假设 RA = 0.4 RB：

δ1 = δD + δB-D = [4.73518839 x 10-9 (0.4 RB) + 4.04203030 x 10-9 RB] = 5.936105657 x 10-9 RB

但是，ΔT=δ1：

0.0001692 m = 5.936105657 x 10-9 RB RB = 28,503.536 N

黄铜杆中的应力

σB = RB/A = 4 (28,503.536 N) / [π (0.03 m)2] = 40,324,254 Pa

因此，σB = 40.324254 MPa

结果比较

黄铜杆中的应力实质上是轴向的。但是，该杆的实体表达以及它的约束方式使它可能发生折弯变形和折弯应力。在真正的桁架中不会出现此行为，这是理论解的基础。为了确保在比较中不包含折弯效应，我们沿杆的中性轴选择一点（在该点处，折弯应力分量为零）。此外，我们不希望检查靠近约束或接触区域的应力，在此类区域，局部效应可能影响结果的准确性。因此，我们将桁架（黄铜杆）的理论轴向应力与黄铜杆质心处 (-300, -150, 0) 的 Fusion 法向 YY 应力结果进行比较。结果中的减号表示应力为压应力，符合预期（而正应力分量表示拉伸应力）：

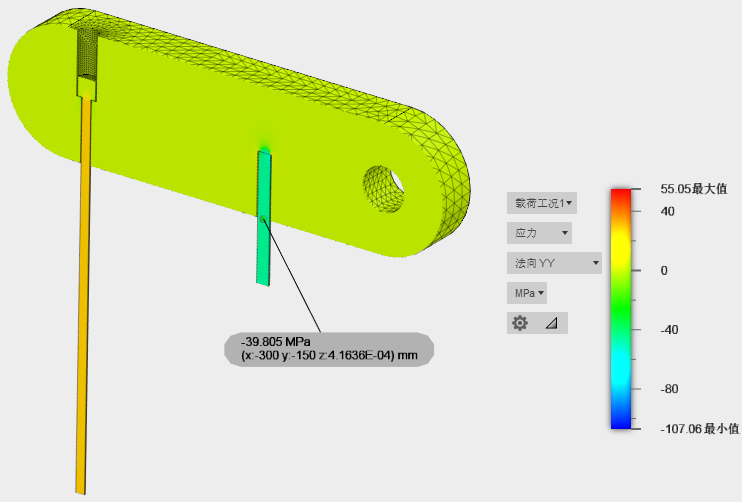
热应力 y 应力图

位置	理论结果（Beer 和 Johnston)	Fusion 结果	差异百分比
黄铜杆的质心	-40.324254 MPa	-39.805 MPa	-1.288 %

注意：您可以将热应力分析结果与理论解之间的差异归于以下因素：

这些杆的接触和受约束端的行为方式没有像真正桁架的端点那样，而是像球联接。在实体表达的端点处可能出现力矩或反常的反作用。
实体杆的横截面面积受网格影响，可能与真正圆柱形横截面的面积不完全一致。
准刚性连杆不是真正刚性。由于沿长度方向折弯以及杆接触区域处的局部受压导致连杆轻微变形，会从一定程度上卸掉这两个杆上的载荷。此效应会减小黄铜杆中的计算应力大小。

尽管理论模型与实体有限元模型之间存在这些已知差异，但结果仍然是非常接近的。

参考

Beer、Ferdinand P. 和 Johnston、Jr., E. Russell，材料力学，McGraw-Hill, Inc.，1981 年，第 58 页，样例问题 2.4。