分析在整个厚度内经历对数温度梯度变化的厚壁圆柱形容器的热应力。

案例描述

该模型是一个圆柱体的八分之一对称表达。在圆柱体的外表面和内表面之间存在 ΔT 的温度差异，内表面比外表面的温度低。圆柱体的末端不受约束。解决方案是有效远离圆柱体的末端。内部温度在整个厚度内呈对数分布（即稳态温度分布）。对于此示例，使用的外半径为 2"，内半径为 1"，温度差异为 10˚F。

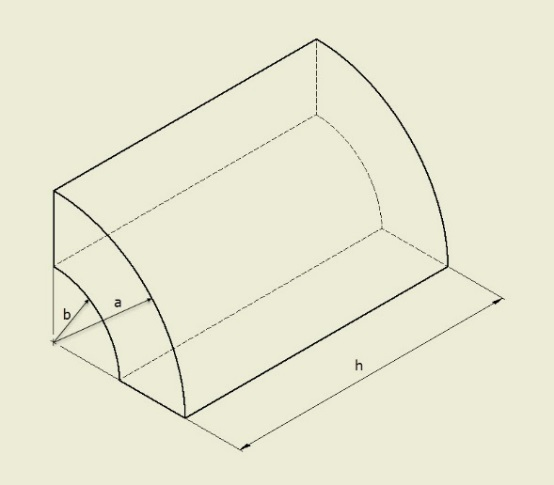
尺寸

• a = 2 英寸
• b = 1 英寸
• h = 4 英寸

分析类型

• 热应力

网格参数

• 网格类型 = 实体，四面体
• 网格大小 = 0.2 英寸，绝对
• 元素顺序 = 抛物线型
• 自适应网格优化：无

材料特性

• 弹性模量 = 3 X 107 psi
• 泊松比 (v) = 0.3
• 热膨胀系数 (α) = 6 x 10-6/°F

约束

• 在以下三个面上的无摩擦约束：
  • 位于 XY 平面中的面（在模型的 -Z 端）
  • 位于 YZ 平面中的面
  • 位于 XZ 平面中的面

载荷

• 圆柱体内部面上的应用温度 = -10°F
• 圆柱体外部面上的应用温度 = -0°F

结果比较

下图中指示的两个角点处的法向 YY 应力张量 (psi)。这两个角点位于两个对称平面的交点处。因此，它们表示完整圆柱体长度的中点，并已从开放端删除。法向 YY 应力对应于圆柱体的切向（圆周）应力。

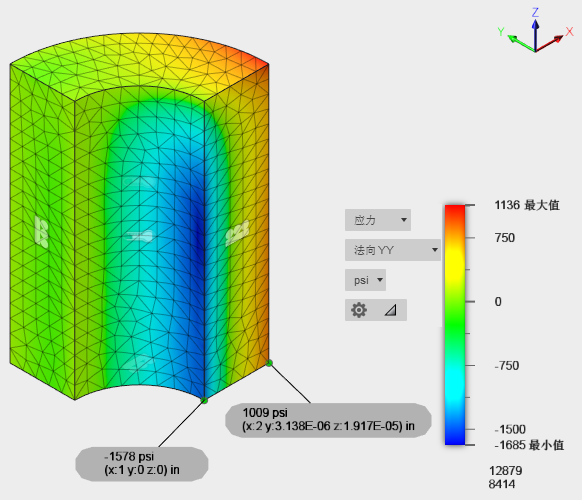
位置	Roark 和杨氏	Fusion	差异百分比
内转角	-1574 psi	-1578 psi	0.25 %
外转角	998 psi	1009 psi	1.10 %

参考

Roark, R. J. 和 Young, W. C.，Roark 的应力和应变公式，第五版，纽约：McGraw-Hill，1975 年，第 585 页，第 15.6 节，案例 16。