Thermische Spannung 02: Quasi-starres Verbindungsstück und zwei Streben

Ermitteln Sie die thermischen Spannungen, die sich entwickeln, wenn die Temperatur eines Profilelements erhöht wird.

Fallbeschreibung

Die Drehachse eines quasi-starren Verbindungsstücks ist eine Bohrung an dessen rechten Ende. Das Verbindungsstück liegt auf einer zylindrischen Messingstange auf. Das linke Ende des Verbindungsstücks ist durch eine zylindrische Stahlstange unten verankert. Die Temperatur der Messingstange wird von 20 °C (die spannungsfreie Temperatur der Baugruppe) auf 50 °C erhöht. Die resultierende thermische Ausdehnung verursacht eine Zugspannung in der fixierenden Stahlstange. Da die Messingstange sich nicht frei ausdehnen kann, entwickelt sich in ihr eine axiale Druckspannung. Wir vergleichen diese axiale Spannung mit der theoretischen Lösung.

Starre Elemente sind beim aktuellen Analysetyp nicht verfügbar. Ein quasi-starres Verhalten wird daher erreicht, indem Sie das Verbindungsstück relativ groß erstellen und die Materialsteifheit auf den maximal unterstützten Wert einstellen. In der folgenden Grafik sind alle Bemaßungen in Millimetern angegeben.

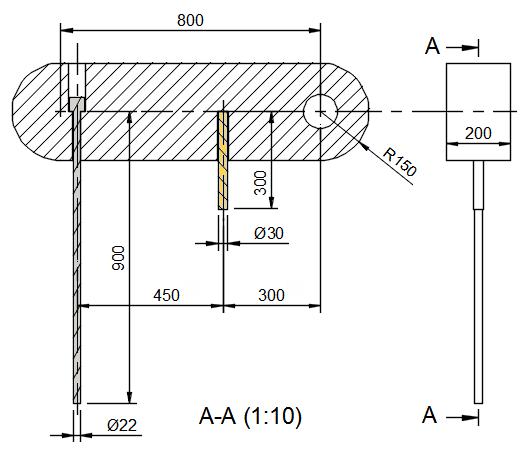
Diagramm zur thermischen Spannung

Bemaßungen (mm)

Studientyp und -parameter

Netzparameter

Materialeigenschaften

Eigenschaft Verknüpfungen Messingstange Stahlstange
Elastizitätsmodul (MPa) 1.3 x 106 105,000 200,000
Poisson-Zahl 0.3 0.31 0.3
Wärmeausdehnungskoeffizient (/ °C) 1.2 x 10-5 1.88 x 10-5 1.2 x 10-5
Anmerkung: Die Wärmeausdehnungskoeffizienten der Stahlstange und des Verbindungsstücks sind nicht von Bedeutung, da diese Bauteile nicht von Temperaturänderungen betroffen sind.

Abhängigkeiten

Anmerkung: Diese Abhängigkeit verhindert, dass sich die Stange um eine Achse dreht, und ermöglicht eine radiale Ausdehnung der Stange aufgrund der Wärmeausdehnung. Daher ist die Stange statisch stabil, und vom Abhängigkeitsschema werden keine künstlichen thermischen Spannungen verursacht.

Thermische Lasten

Kontaktparameter

Die Bohrungen im Verbindungsstück für beide Stangen haben eine entsprechende Größe für ausreichend Spiel. Daher findet nur an zwei Stellen ein Kontakt statt:

Die Einstellungen für beide Kontaktsätze lauten wie folgt:

Anmerkung: Auf alle drei Körper wird eine Temperatur angewendet, um die Messingstange heißer zu machen und um sicherzustellen, dass die Temperaturen der anderen beiden Bauteile die spannungsfreien Werte beibehalten. Um den Wärmestrom an den Kontaktpunkten der Bauteile zu minimieren, ist eine Wärmeleitfähigkeit von null wünschenswert. Bei einer Leitfähigkeit von null schlägt die Lösung jedoch fehl. Daher geben wir einen sehr kleinen Leitfähigkeitswert an.

Theoretische Lösung

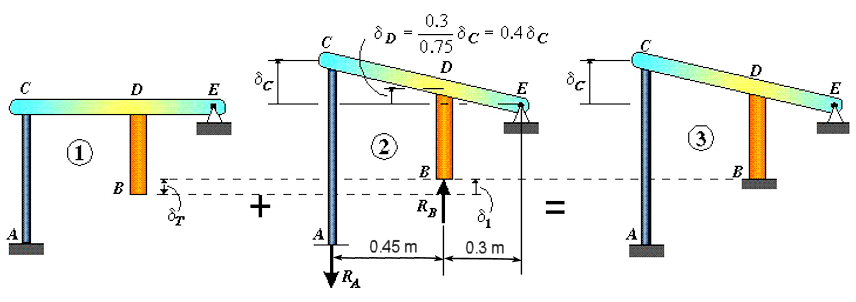
Diagramm zur thermischen Spannungstheorie

Unter Berücksichtigung der vorherigen Grafik erhalten wir die folgende Beziehung aus der Beer- und Johnston-Referenz:

ΣME = 0 RA * (0.75 m) - RB * (0.3 m) = 0 RA = 0.4 RB

Verformungen

Die Methode der Überlagerung wird verwendet. Wenn RB entfernt wird, führt der Temperaturanstieg des Zylinders dazu, dass Punkt B um die Entfernung δT nach unten verschoben wird. Die Reaktion RB bewirkt eine Verschiebung δ1 der gleichen Größe wie δT, sodass die endgültige Verformung von Punkt B null ist.

Aufgrund eines Temperaturanstiegs von 30 °C (50 °C - 20 °C) verlängert sich die Messingstange, sofern sie nicht abhängig ist, entsprechend der folgenden Gleichung um δT:

δT = L(ΔT)α = (0.3 m)(30 °C)(1.88 x 10-5/°C) = 0.0001692 m

Beachten Sie, dass δD = 0.4 δC und δ1 = δD + δB-D ist, wobei δB-D die Längenänderung der Messingstange ist.

δC = RAL / (AE)

Wenn für die Stahlstange gilt: L = 0.9 m, A = πD2/4, D = 0.03 m und E = 105 x 109 Pa:

δC = 4 RA(0.9 m) / [π(0.03 m)2(105 x 109 Pa)] = 11.83797097 x 10-9 RA δD = 0.4 δC = 0.4 (11.83797097 x 10-9 RA) = 4.73518839 x 10-9 RA δB-D = RBL / (AE)

Wenn für die Messingstange gilt: L = 0.3 m, A = πD2/4, D = 0.022 m und E = 105 x 109 Pa:

δB-D = 4 RB(0.9 m) / [π(0.03 m)2(105 x 109 Pa)] = 4.04203030 x 10-9 RB

Sei RA = 0.4 RB:

δ1 = δD + δB-D = [4.73518839 x 10-9 (0.4 RB) + 4.04203030 x 10-9 RB] = 5.936105657 x 10-9 RB

Jedoch gilt δT = δ1:

0.0001692 m = 5.936105657 x 10-9 RB RB = 28,503.536 N

Spannung in der Messingstange

σB = RB/A = 4 (28,503.536 N) / [π (0.03 m)2] = 40,324,254 Pa

Daher ergibt sich σB = 40.324254 MPa

Ergebnisvergleich

Die Spannung in der Messingstange ist im Wesentlichen axial. Die Volumenkörperdarstellung der Stange und die Art der Abhängigkeit ermöglichen es jedoch, dass eine Biegeverformung und Biegespannungen auftreten. Dieses Verhalten tritt bei einer echten Strebe nicht auf, was die Basis der theoretischen Lösung ist. Um sicherzustellen, dass wir keine Biegungseffekte in unseren Vergleich integrieren, wählen wir einen Punkt entlang der neutralen Achse der Stange aus (wobei die Biegespannungskomponente null ist). Darüber hinaus wollen wir keine Spannungen in der Nähe einer Abhängigkeit oder Kontaktfläche prüfen, wo die Ergebnisse möglicherweise durch lokale Effekte verzerrt werden. Daher vergleichen wir die theoretische axiale Spannung der Strebe (Messingstange) mit dem lotrechten YY-Spannungsergebnis von Fusion am Schwerpunkt der Messingstange (-300, -150, 0). Das Minuszeichen des Ergebnisses gibt an, dass es sich, wie erwartet, um eine Druckspannung handelt (positive Spannungskomponenten sind Zugspannungen):

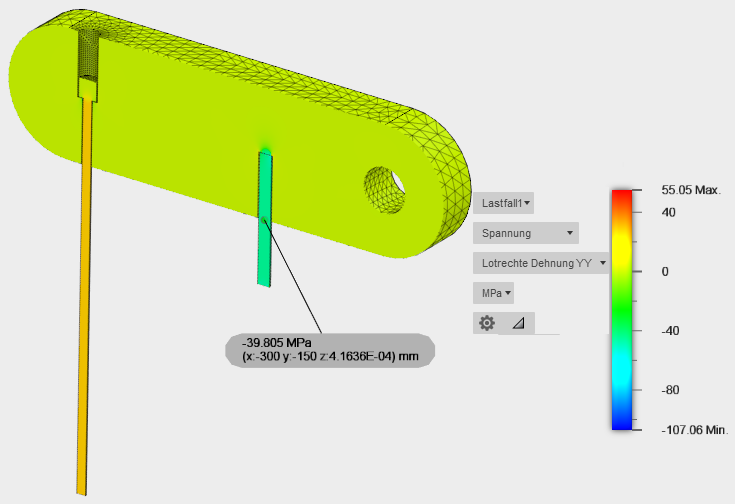
Diagramm zur thermischen Spannung (Y-Spannung)

Position Theoretisches Ergebnis (Beer und Johnston) Fusion Ergebnis Prozentuale Differenz
Schwerpunkt der Messingstange -40.324254 MPa -39.805 MPa -1.288 %
Anmerkung: Sie können die Differenz zwischen den Ergebnissen der thermischen Spannungsstudie und der theoretischen Lösung auf die folgenden Faktoren zurückführen:

Trotz dieser bekannten Unterschiede zwischen den theoretischen und Finite-Element-Volumenkörpermodellen sind die Ergebnisse dennoch ziemlich genau.

Referenz

Beer, Ferdinand P. und Johnston, Jr., E. Russell, Mechanics of Materials, McGraw-Hill, Inc., 1981, Beispielproblem 2.4, Seite 58.

Übergeordnete Seite: Genauigkeitsprüfung für thermische Spannung