3.4 ULS Capacity And Stresses Of An RC Section

Subjects Covered

• Reinforce faces
• 1 bar by 2 covers
• Nominal Load
• Gamma factors
• Biaxial bending
• ULS Shear design
• Iterations fail to converge

Outline

Ultimate limit state section capacities, for moments and axial force, are to be calculated for two of the sections defined in section 2 as follows:

Precast Section	Calculate
	This precast section has 7no. 25mm bars in the bottom faces with 50mm cover. The end bars have 50mm cover to the vertical faces. Additionally, 2no. 16mm bars are placed in the top of the upstand with 50mm cover to both faces. The precast beam is lifted at its ends through the centroid of the section which generates a nominal My bending moment of 218kNm due to its self weight (Gamma ULS = 1.35). Check that the My ULS capacity of the section exceeds this. What is the angle of the neutral axis? The precast beam is stitched to a continuous insitu slab which forces the neutral axis to be horizontal. What is the My ULS capacity now? By keeping the neutral axis horizontal there is an out of balance Mz moment which is resisted by a transverse membrane force in the slab. What is the value of this force if the beam is 10m long? Save this section for use in other examples.
	This column has a characteristic concentric axial load of 1000kN together with a characteristic Mz moment of 100kNm. What is the maximum additional characteristic My moment that can be applied at ULS. (Gamma ULS = 1.35). The design moments and forces at ULS are My = 350kNm, Axial = 1320kN, Shear along z = 180kN. What links of 10mm diameter are required? At what value of shear force will it be necessary to have additional links?

Procedure

Start the program and use the Home Open button to open the file “My EU Example 2_1.sam” created in example 2.1.

Section 1

1. Use the menu item File | Titles to change the Section Title to “Grillage Edge Section with Reinforcement”, the Sub-title to “Example 3.4a” and the Job Number to “3.4a”. Click ✓ OK to close the Titles form.

Define Reinforcement

2. Open the Define Reinforcement form by clicking on the “Reinforcement” object in the Design Section navigation window

3. Click on the Generate drop down menu and select “Reinforce Face(s)” from the list.

4. Click in the No. Of bars field and enter a value of “7”.

5. Click in the Diameter field and enter a value of “25mm”.

   

6. Click on the sloping bottom face of the section on the graphics window. The face will be highlighted in red and the Reinforcement along face(s) form will open.

   

7. Click in the No. of faces field and enter a value of “2” (the default cover of 50mm is assumed) then click ✓ OK

8. Click on the Generate drop down menu and select “1 bar by 2 covers” from the list.

9. Click in the Diameter field and enter a value of “16mm”.

10. Click on the left hand vertical and the top curved faces of the section on the graphics window. Both faces will be highlighted in red and the Locate bar by 2 covers form will open.

11. Enter values of “50mm” in both the Cover to face 1 and Cover to face 2 fields then click ✓ OK

12. Repeat steps 10 and 11 for the top right hand corner.

13. Click ✓ OK to close the Define Reinforcement form.

Define Applied Forces

14. For bridge structures it is possible to define the various components of load effects to assemble a valid EN 1990 combination with automatically applied load and psi factors. To do this the correct bridge type must be assigned to the section. This is done on the Section Overview form which can be accessed from the File | Section Overview menu item.

    

15. Set the Bridge Type to be “Road” from the dropdown list.

16. Use the toolbar button at the top of the Design Section navigation window to create a new loadcase... which will open the Define Loadcase form.

17. Click on the other “+” button near the bottom of the form to add a row to the table. On the first row of the table, click in the Type column and select “Y Moment” from the drop down list.

18. Enter a value of “218kNm” in the Characteristic Effect column.

19. Enter a value of “1.35” in the Ultimate | γ column.

    

20. Click ✓ OK to close the Define loads form.

Calculate Capacity

21. Use the toolbar button dropdown in the Design Section navigation window to select “Bending Axial & Shear” which will open the Bending, Axial and Shear form. Ensure that Analysis type is set to “ULS Persistent/Transient”.

22. Click on the Loadcase drop down menu and select “SL1: Loadcase” from the list.

23. Click on the Resistance drop down menu and select “Y Moment – Positive” from the list.

24. Click on the Neutral Axis angle drop down menu and select “Free” from the list.

25. The limiting additional load is 174.01kNm. The neutral angle axis is 35.2°.

    

26. Click on the Neutral Axis angle drop down menu and select “Fixed horizontal” from the list. The limiting additional load is now 503.9kNm.

27. The associated Mz moment is -561.1kNm but this bending will be restrained by the membrane action in the adjoining slab. If this is the centre section of a 10m ling beam and we assume a uniformly distributed membrane force acting in the interface between the edge beam and slab it will be 8* Mz/L2 = 45kN/m and will be compressive.

28. Click ✓ OK to close the Bending, Axial and Shear form.

29. Save the data file as “My EU Example 3_4a.sam” using the main menu item File | Save As.

Section 2

30. Open the existing file “EU Example 2_3.sam”, created in section 2.3 of this manual, by selecting the menu item File | Open.
31. Use the menu item File | Titles to change the Sub-title to “Example 3.4b” and the Job Number to “3.4b”.
32. Click on ✓ OK to close the Titles form.

Define Applied Actions

33. Open the Define loadcase form using the toolbar button at the top of the Design Section navigation Window and select “Loadcase...”.

34. Click on the “+” (Insert record) button near the bottom of the form twice to add 2 rows to the table. On the first row of the table, click in the Type column and select “Axial” from the drop down list. In the Action field select “User Defined”. In the Characteristic Effect field and enter a value of “1000kN”.

35. On the second row of the table on the Define loads form, click in the Type column and select “Z Moment” from the drop down list. In the Action field select “User Defined”. Enter a value of “100kNm” in the Characteristic Effect column.

36. For all rows in the table, enter a value of “1.35” in the Ultimate γ column.

37. Change the Loadcase name to “ULS Capacity” and then click on ✓ OK to close the Define loadcase form.

38. Use the toolbar button dropdown in the Design Section navigation window to open the Bending, Axial and Shear form. Ensure that Analysis type is set to “ULS Persistent/Transient”.

39. Click on the Loadcase drop down menu and select “ULS Capacity” from the list.

40. Click on the Resistance drop down menu and select “Y Moment – Positive” from the list.

41. The maximum additional Design My moment that can be applied is 473.88kNm. The max characteristic moment is therefore 473.88/1.35 = 351.02kNm.

42. Click on the ✓ OK button to close the Bending, Axial and Shear form.

43. Create an additional loadcase using the toolbar button at the top of the Design Section navigation Window and change the name to “ULS Shear”.

44. The ULS design moment (as opposed to nominal moments) are entered directly into the top part of the table. In the My column (under the Ultimate group) enter “350”. Enter “1320” in the Ax column and enter “180” in the Vz column.

    

45. Click ✓ OK to close the Define loads form. There should now be the two loadcases shown in the navigation window

46. Use the toolbar button dropdown in the navigation window to open the Bending, Axial and Shear form.

47. In this form click on the Resistance drop down menu and select “Not used”. Select “SL2: ULS Shear” in the Loadcase field.

48. Tick the Shear Force Calcs check box.

49. Click on the Results... button to display the Results Viewer.

50. Scroll to the bottom of the Results Viewer to find the Link arrangement. The links of 10mm diameter that are required at 347.78 for 2 legs and 695.56mm for 4 legs.

    

51. Minimum reinforcement only is required because V Ed < V_Rd,c ( V Ed = 180kN and V_Rd,c = 248.73). These values can be seen on the Bending, Axial and Shear form. If the actual shear force exceeds this value then additional links will be required. The shear force must always be below 506.63kN no matter how much shear reinforcement is required.

    

52. Click ✓ OK to close the Bending, Axial and Shear form.

53. Save the data file as “My EU Example 3_4.sam” using the main menu item File | Save As.

Section 3

54. Open the supplied data file “EU Example 3_4c.sam” via the menu item Help | Tutorials | Open Tutorial Model. In the Materials navigation window you will see that there are two concrete materials and a reinforcement material. The concrete material that is assigned to the section is the grade C35/45 with a rectangular stress block.

55. Use the toolbar button dropdown in the Design Section navigation window to open the Bending, Axial and Shear analysis form.

56. Ensure that Analysis type is set to “ULS Persistent/Transient”.

57. Click on the Resistance drop down menu and select “Y Moment - Positive” from the list and ensure that the Loadcase field is set to “None”.

58. The iterative procedure fails to converge and a warning message is displayed.

    

59. Click on the ✓ OK button in the warning window and the Control Iterations form is displayed. Note: when considering rectangular stress blocks it is inherently difficult for the iterations process to converge to a solution using the strain compatibility methods. We need to reduce the out of balance Mz bending moment and axial force to values that are as close to zero as possible to obtain an approximate solution. This can be achieved by manually controlling the iterations as follows.

60. First of all set the Max strain to the compressive limit, which is usually 0.0035 for flexure calculations. Then use the arrowed buttons to reduce the minimum strain in increments set by the Spin Increment. You will graphically see the neutral axis moving up and the residual Internal Axial force reducing. Continue with this until the axial force just changes sign as shown below.

    

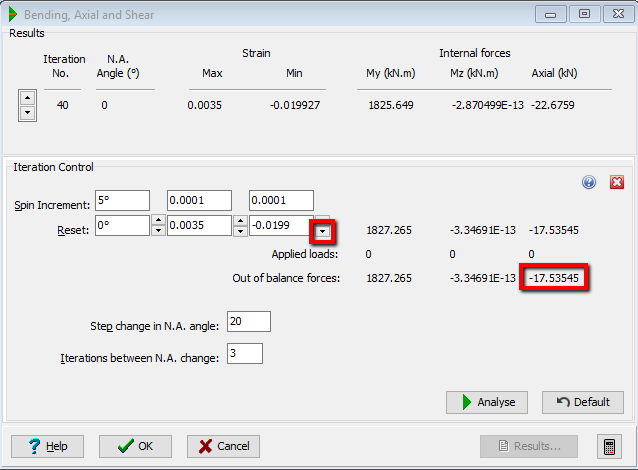
61. The Spin increment needs to be reduced so that more refined adjustments can be made to the residual axial internal force. Input a value of “0.000001” in the Strain / Min / Spin Increment field and click on the arrowed buttons to reduce the minimum strain further to the value shown below.

    

However, we cannot get any printed results for this so if these are needed then we need to look at different solutions. Some suggestions are shown below:

• Adjust the iteration tolerance to a value that results in a converged solution (in this case the out of balance force at the “failure to converge” is 22.77kN – as can be seen at the top of the analysis form – so a tolerance of 25kN should work
• Try ignoring the compression reinforcement by ticking the appropriate box on the analysis form
• Change the material stress strain relationship to either bi-linear or rectangular-parabolic so there is no abrupt change in concrete stress.

62. To change the iteration tolerance the following steps can be taken:

• Right mouse click anywhere in the Design Section navigation widow and select “Tolerance” to open the Convergence Tolerance form. Set the value in the Axial field to “25” and click ✓ OK to close the form.
• Re-open the Bending, Axial and Shear analysis form and the iterations converge to a solution where the My capacity is the Limiting additional load. This then allows the Results... button to be used to get some printable results. Click ✓ OK on the Bending, Axial and Shear form after the results have been inspected/saved etc..
• Close the program.

Summary

This example illustrates four techniques:

1. How to calculate section capacities of a non symmetrical section where natural bending occurs about a principle axis.
2. How to restrain a section so that bending occurs about a given axis and the resultant (out of balance) moments about a perpendicular axis can be determined.
3. Consideration of biaxial bending combined with axial forces when applying a given set of forces and moments to a section and being able to calculate the allowable addition forces and moments.
4. How to design shear link requirements in a column.

In addition, it shows what happens if a section fails to converge in its iterative solution and some of the procedures that may be used to resolve this problem.