Hyperelastic materials theory

The nonlinear stress-strain characteristics of hyperelastic materials, such as rubber, are complex. The many available grades of material vary widely in behavior. For nonlinear simulations in Fusion, hyperelastic materials are represented using the 2-constant standard Mooney-Rivlin material model. The material coefficients are derived by curve-fitting experimentally obtained raw stress-strain data. This data may be based on various tests, including the following tension/compression test examples:

Uniaxial (1 and 2)
Planar
Equi-biaxial
Biaxial
Confined
Triaxial
Volumetric

The description of these tests and the raw data they produce is beyond the scope of this topic. The material tests are performed by labs specializing in the process, and the curve-fitting must be done outside of Fusion. (The program does not have a built-in facility for accepting the raw data and performing the curve-fitting function.) There are various programs available for performing the necessary curve-fitting function once the raw data is obtained. One such program is HyperFit, which is available in a freeware demo version (limited functionality) and a licensed version. A full license is required to generate the curve and resultant material constants.

The Mooney-Rivlin Hyperelastic Material Model

Hyperelastic materials in Fusion are modeled using the 2-constant standard Mooney-Rivlin material model. The nearly incompressible formulation is used, so volumetric terms are included in the strain energy function. The effects of shear distortion and volumetric deformation are separated.

General Mooney-Rivlin Strain Energy Function

The relationship between the strain energy, shear distortion, and volumetric deformation is expressed in the following general case function (applicable to the 2-constant and higher-order cases):

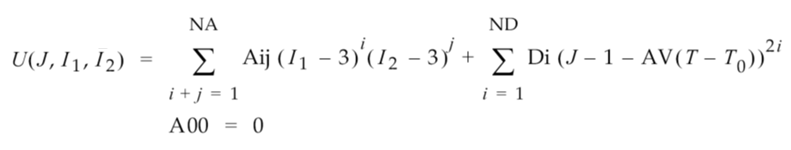
mooney-rivlin strain energy function

Where:

U is the strain energy.
I1 is the first distortional strain invariant.
I2 is the second distortional strain invariant.
J = det F, which is the determinate of the deformation gradient.
Aij is the set of material constants related to shear distortion (i and j being the subscripts of the individual constants).
Di is the set of material constants related to volumetric deformation.
AV is the volumetric coefficient of thermal expansion.
T is the current temperature
T0 is the initial temperature

Simplified 2-Constant Mooney-Rivlin Equation

Currently, Fusion does not support thermal effects for hyperelastic materials in nonlinear analyses. Therefore, we can simplify the preceding function by eliminating the thermal expansion terms (AV, T, and T0) and working out the summation for the constants Fusion accepts (A01, A10, and D1). The simplified strain energy equation then becomes as follows:

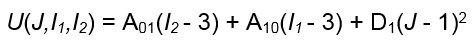
simplified 2-constant mooney-rivlin equation

Where:

U, J, I1, and I2 are as previously defined.
A01 is the first of two distortional constants related to shear deformation of the material.
A10 is the second of two distortional constants related to shear deformation of the material.
D1 is the constant related to volumetric deformation of the material, which is equal to half of the bulk modulus (K).

That is, 2D1 = K. Therefore, D1 = K/2

Note: The two distortional constants (A01 and A10) and the volumetric deformation constant (D1) are the values you define when creating a hyperelastic material in your material library. These are the values you must obtain externally by curve-fitting the raw material test data. In some publications, the A01 and A10 constants are referred to as C01 and C10, respectively.