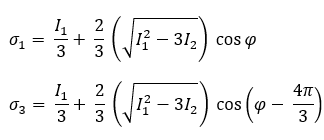Principal Stress calculations

Stresses can be calculated based on a set of axes that differ from the global X, Y, and Z directions. We can rotate the coordinate system so that only normal stresses remain, and all shear stresses are zero. At this orientation, the normal vector of a surface and the stress vector acting on that surface are collinear. Then, the direction of the normal vector is called the principal stress direction. The magnitude of the stress vector on the surface is called the principal stress value. There are three principal stress values: 1st, 2nd, and 3rd Principal Stress. These values are often called the Maximum, Intermediate, and Minimum Principal Stress, respectively.

The mathematical equations for determining the principal stresses (σ1 and σ3) are more tedious than the previously given von Mises stress equation. We must first determine the angle of rotation (φ), in radians, between the global and principal axes:

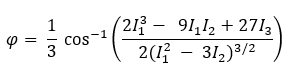
where I1, I2, and I3 are stress invariants determined by the following equations:

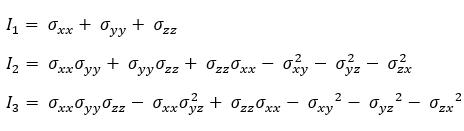
Finally, the first and third principal stresses are determined by the following equations: