Quasi-static event simulation theory

This theoretical background is true for both dynamic and quasi-static event simulations.

Event Simulations combine the principles of Hooke's Law (F=-kx) and Newton's 2nd Law (F=ma). After combining these two equations by eliminating the force term, we arrive at ma + kx = 0. Now we can add the effects of damping (F=-cv) to arrive at the general equation of motion:

ma+cv+kx = 0

where m is the mass, a is the acceleration, c is a damping coefficient, v is the velocity, k is the stiffness, and x is the displacement. In matrix form, this equation is represented as:

[M]{a} + [C]{v}+[K]{x} = 0

From this foundational equation, stresses and strains can be determined with the use of the displacement vector {x} and the constitutive laws governing the material response.

Central Difference Time Integration

Event Simulations use an explicit solver built on the central difference time integration algorithm. This algorithm uses knowledge of two previous states to directly resolve the current state (displacement, velocity, and acceleration). The size of the step from one state to the next is driven by the Courant stability limit (stable step increment), which governs the largest allowable step, beyond which the solution will fail. When the effects of damping are considered, this is expressed as:

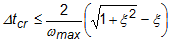
Where Δtcr is the stable step increment, ωmax is the largest natural frequency in the mesh, and ξ is the fraction of critical damping in the highest mode.

Generally speaking, stable step increments in a quasi-static event simulation are very small. The explicit solver is very efficient and can handle material and contact nonlinearities with relative ease because no stiffness matrix has to be formed at each iteration. Nodal accelerations can be solved directly.