Teoría de materiales hiperelásticos

Las características no lineales de tensión-deformación de los materiales hiperelásticos tales como el caucho son complejas. El comportamiento de los numerosos grados de material que están disponibles varía considerablemente. En las simulaciones no lineales de Fusion, los materiales hiperelásticos se representan mediante el modelo de material Mooney-Rivlin estándar de 2 constantes. Los coeficientes de los materiales se derivan de datos de tensión-deformación sin procesar obtenidos de forma experimental en el ajuste de curvas. Estos datos se pueden basar en diversas pruebas, como los siguientes ejemplos de pruebas de tensión/compresión:

• Uniaxial (1 y 2)
• Plana
• Equi-biaxial
• Biaxial
• Confinado
• Triaxial
• Volumétrico

La descripción de estas pruebas y los datos originales que se producen no forman parte del objetivo de este tema. Las pruebas de materiales las llevan a cabo laboratorios especializados en el proceso, y el ajuste de curvas se debe realizar fuera de Fusion. (El programa no tiene una función integrada para aceptar los datos sin procesar y ajustar curvas). Hay varios programas disponibles para esta función de ajuste de curvas necesaria cuando se hayan obtenido los datos originales. Uno de estos programas es HyperFit, que está disponible en una versión demo gratuita (funcionalidad limitada) y en una versión con licencia. Se necesita una licencia completa para generar las constantes del material resultante y la curva.

Modelo de material hiperelástico de Mooney-Rivlin

Los materiales hiperelásticos de Fusion se llevan a cabo mediante el modelo de Mooney-Rivlin estándar de 2 constantes. Se utiliza la formulación casi incompresible, por lo que los términos volumétricos se incluyen en la función de la energía de deformación. Los efectos de la distorsión de corte y la deformación volumétrica se separan.

Función general de energía de deformación de Mooney-Rivlin

La relación entre la energía de deformación, la distorsión de corte y la deformación volumétrica se expresa con la siguiente función general (aplicable a los casos de 2 constantes y de mayor orden):

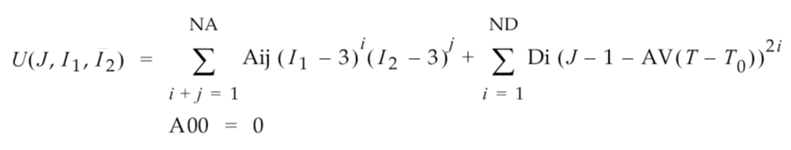
Donde:

• U es la energía de deformación.
• I1 es la primera deformación invariable que provoca distorsión.
• I2 es la segunda deformación invariable.
• J = det F, que es el determinante del gradiente de deformación.
• Aij es el conjunto de constantes del material relacionadas con la distorsión de corte (i y j son los subíndices de las constantes individuales).
• Di es el conjunto de constantes de material relacionadas con la deformación volumétrica.
• AV es el coeficiente volumétrico de expansión térmica.
• T es la temperatura actual
• T0 es la temperatura inicial

Ecuación simplificada de 2 constantes de Mooney-Rivlin

Actualmente, Fusion no admite efectos térmicos para materiales hiperelásticos en análisis no lineales. Por lo tanto, podemos simplificar la función anterior eliminando los términos de expansión térmica (AV, T y T0) y calculando la suma de las constantes que acepta Fusion (A01, A10 y D1). La ecuación simplificada para la energía de deformación queda así:

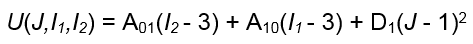
Donde:

• *U, J, I1* y I2 se han definido previamente.
• A01 es la primera de las dos constantes de distorsión relacionadas con la deformación de corte del material.
• A10 es la segunda de las dos constantes de distorsión relacionadas con la deformación de corte del material.
• D1 es la constante relacionada con la deformación volumétrica del material, que es igual a la mitad del módulo de masa (K).

Es decir, 2D1 = K. Por lo tanto, D1 = K/2