Simulation d’événements 02
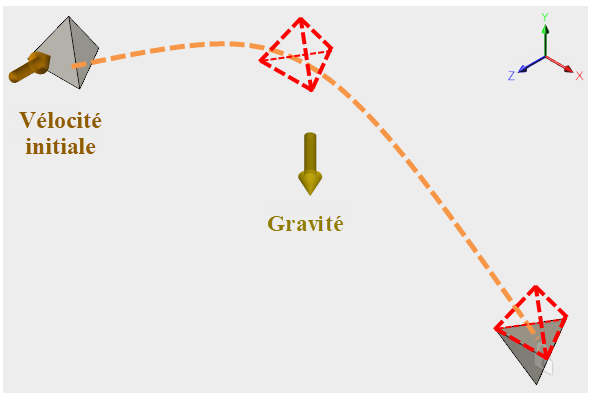
Trajectoire parabolique d’un projectile.
Description du cas
Cet exemple de vérification de la précision montre la fiabilité du solveur de simulation d'événements pour quantifier les trois phénomènes suivants :
- Vitesses linéaires initiales
- Grands déplacements des corps libres (dynamiques des mouvements)
- Accélération et décélération gravitationnelles
Le modèle est constitué de deux corps tétraédriques à élément unique : un corps amovible (Projectile) et un corps fixe (Stationnaire). Le corps fixe est également défini en tant que corps rigide, ce qui signifie qu’il ne se déforme pas du tout. En outre, les corps n'interagissent pas les uns avec les autres (aucun contact). Le corps fixe est uniquement là comme référence de position. Plus précisément, le corps fixe est placé de telle sorte que sa surface supérieure corresponde exactement à l'emplacement théorique de la surface inférieure du corps du projectile à la fin de la simulation d'événement.
Deux composants égaux de vitesse linéaire, un vertical et un horizontal, sont appliqués au corps du projectile en tant que condition initiale. En d'autres termes, la vitesse initiale résultante est à un angle ascendant de 45° par rapport à la direction horizontale. Cet angle, en théorie, permet d'obtenir la plus grande distance horizontale de déplacement d'un projectile pour une vitesse initiale donnée (en ignorant la résistance au vent). Les résultats suivants sont déterminés en théorie et comparés aux résultats de la simulation d’événements Fusion :
- Hauteur du projectile lorsque sa vitesse verticale atteint zéro et s'inverse (hauteur maximale le long de la trajectoire du projectile)
- Temps nécessaire pour atteindre la hauteur maximale du projectile
- Temps nécessaire pour que le projectile revienne à son élévation initiale (retour au sol)
- Distance horizontale traversée par le projectile lorsqu’il atteint à nouveau l’élévation initiale
Type et paramètres de l'étude
- Simulation d'événements
- Durée totale de l'événement = 0,2 seconde
- Nombre d'intervalles d'enregistrement des résultats = 20 (produit d'un jeu de résultats par 10 millisecondes)
- Critères de suppression d’éléments : Aucun défini
Corps rigide
- Le corps Stationnaire est rigide.
Géométrie de modèle
- Description : Deux tétraèdres identiques, toutes les longueurs d'arête = 0,866 pouce, tous les angles des coins des faces = 60°
- Le corps fixe est positionné horizontalement à une distance de 7,722 pouces de l'emplacement initial du corps du projectile. En outre, le corps fixe pivote de sorte que sa face supérieure corresponde à l'emplacement théorique de la face inférieure du corps du projectile à la fin de l'événement.
Paramètres de maillage
- Type de maillage = Solide, Tétraédrique
- Ordre d'élément = parabolique
- Taille du maillage = 1,0 pouce, absolue (résultant en un seul élément par pièce, maximisant le pas de temps de calcul admissible et minimisant le temps de calcul)
- Affinement du maillage adaptatif : aucun
Propriétés du matériau
Les propriétés du matériau n'ont pas d'incidence sur la physique du mouvement du projectile. Toutefois, une pièce à densité plus élevée résout plus rapidement qu’une pièce à densité inférieure pour les simulations d’événements. Par conséquent, la matière Plomb a été sélectionnée, car elle a une densité relativement élevée.
- Module d’élasticité = 2,031 X 106 psi
- Densité = 0,4097 lbmass/in3
- Coefficient de Poisson (v) = 0,3
Contraintes
- Le corps stationnaire est entièrement fixe
Charge
Gravité : accélération = 32,174 ft/sec2 dans la direction -Y
Vitesse linéaire initiale :
Dans la direction X : 3,2174 pi/s
Dans la direction Y : 3,2174 pi/s
Remarque : vous devez modifier le paramètre Précision générale par défaut de 0,123 à 0,1234 pour afficher le quatrième nombre décimal des composants à la vitesse initiale. Recherchez ce paramètre dans la section Affichage des unités et des valeurs de la boîte de dialogue Préférences.
Résultats théoriques
Temps nécessaire pour que la vitesse verticale atteigne zéro
Temps 1 = Vitesse initiale (composant vertical) / Taux de décélération
`Time1 = (3,2174 pi/s) / (32,174 pi/s2) = 0,1 s (correspond à l’étape 10 de la simulation des événements)
Heure à laquelle le projectile revient à l’élévation d’origine
Le temps de retour à partir de la hauteur d'origine à partir de la hauteur maximale est égal au temps pour atteindre la hauteur maximale à partir de la position initiale. Par conséquent :
Time2 = 2 * Time1
Time2 = 2 * 0,1 s = 0,2 s (correspond à l’étape 20 de la simulation d’événement)
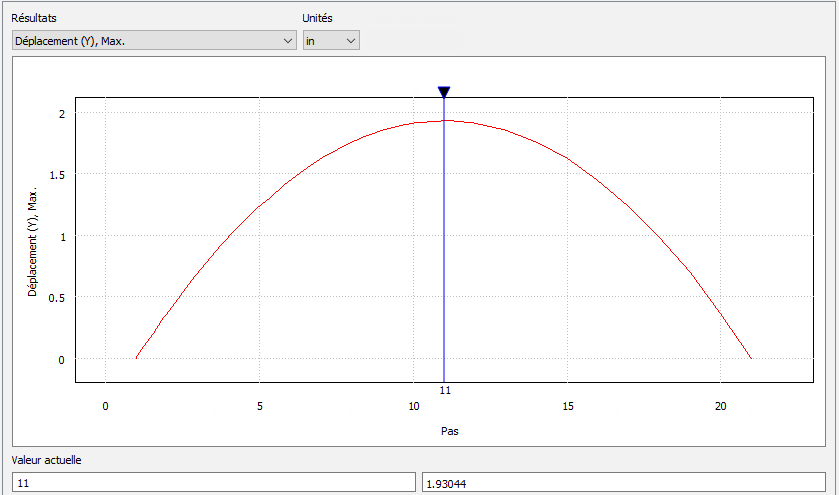
Hauteur maximale du projectile par rapport à la position initiale (déplacement Y)
Hauteur maximale = Vitesse Y moyenne * Temps1
Vitesse Y moyenne (po/s) = (12 po/pi) * Vitesse Y initiale (pi/s) / 2 = (12 po/pi) * (3,2174 pi/s) / 2 = 19,3044 po/s
Hauteur maximale = 19,3044 po * 0,1 s = 1,93044 po
Distance horizontale du projectile à la fin de l’événement
Sans résistance au vent ni aucune autre force opposée, la composante de vitesse horizontale reste constante. Par conséquent :
Distance horizontale (po) = (12 po/pi) \* Vitesse X initiale (pi/s) \* Temps2 = (12 po/pi) \* (3,2174 pi/s) \* 0,2 s = 7,72166 po
Comparaison des résultats
Augmentez la précision de la légende pour comparer les résultats à la théorie pour plus de décimales. Plus précisément, accédez à la section Affichage des unités et des valeurs de la boîte de dialogue Préférences. Remplacez la valeur 1.123 du paramètre Précision générale par 1.12345. Dans Affichage des unités et des valeurs > Simulation et Generative Design, modifiez le paramètre Précision de la notation scientifique de 1.123E+04 à 1.12345E+04. La légende affiche alors cinq décimales pour les résultats de notation décimale et scientifique.
| Résultat | Théorie | Fusion | Différence |
|---|---|---|---|
| Temps1 (lorsque le déplacement Y de pointe est atteint) |
0,1 s | 0,1 s | 0 % |
| Déplacement maximum en Y | 1,93044 po | 1,93044 po | 0 % |
| Temps2 (lorsque le projectile revient à l’élévation d’origine) |
0,2 s (correspond à l’étape 20) |
0,2 s (correspond à l’étape 20) |
0 % |
| Déplacement Y au temps2 | 0 po | -3,30358 x 10-5 po | -3,30358 x 10-5 po |
| Déplacement X au Temps2 | 7,72166 pouces | 7,72179 pouces | 0,0017 % |
Référence
Les caractéristiques physiques newtoniennes de base (équations de mouvement) sont disponibles à partir de nombreuses sources de référence.