Simulation d’événements 01
Déformation plastique de la sphère épaisse creuse avec pression interne.
Description du cas
Cet exemple de vérification de la précision montre la fiabilité du solveur de simulation d'événements pour quantifier les trois phénomènes suivants :
- Charges appliquées temporelles
- Comportement du matériau non linéaire, notamment la déformation plastique lorsqu'il est chargé au-delà de la limite d'élasticité
- Utilisation de la symétrie pour déterminer le comportement d'un corps complet en utilisant uniquement une représentation partielle, beaucoup plus petite
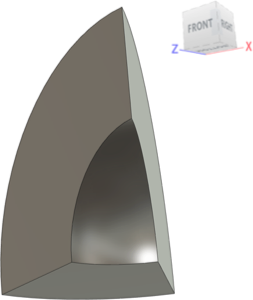
Le modèle est une représentation symétrique d'un seizième de la sphère creuse épaisse. Une pression uniforme est appliquée à la surface intérieure de l'empreinte. La magnitude de la pression augmente de façon linéaire. À un certain point de l'événement, la déformation plastique commence à se produire sur la surface intérieure. Au fur et à mesure que la simulation se poursuit, une plus grande partie de l'épaisseur de la paroi atteint progressivement les niveaux de contrainte plastique. Finalement, la surface extérieure atteint la limite d'élasticité, à laquelle la sphère commence à se développer rapidement. La dérivation des pressions nécessaires pour atteindre l'état du plastique sur les surfaces intérieures et extérieures est présentée sur cette page. Les résultats de Fusion sont comparés aux résultats théoriques.
On suppose une matière plastique parfaite, ce qui signifie que l'inclinaison de la courbe contrainte-déformation est plate (zéro) une fois la limite d'élasticité effectuée. En d'autres termes, il n'y a pas d'écrouissage du matériau. Cette hypothèse simplifie la dérivation théorique.
Les supports sans frottement représentent les conditions de symétrie sur chaque surface découpée (plate) de la sphère creuse.
Type et paramètres de l’étude
- Simulation d'événements
- Durée totale de l'événement = 0,051 seconde
- Nombre d'intervalles d'enregistrement des résultats = 51 (produisant un jeu de résultats par milliseconde)
- Critères de suppression d’éléments : Aucun défini
Géométrie de modèle
- Description : un huitième de sphère creuse (un huitième ou un segment de 45° d'un hémisphère creux)
- Rayon intérieur de la sphère = 2 pouces
- Rayon externe de la sphère = 4 pouces
- Épaisseur de paroi = 2 pouces
Paramètres de maillage
- Type de maillage = Solide, Tétraédrique
- Ordre d'élément = parabolique
- Taille du maillage = 0,333 pouce, absolu
- Affinement du maillage adaptatif : aucun
Propriétés du matériau
- Module d'élasticité = 3,0 X 107 psi
- Densité = 0,284 lbmass/in3
- Coefficient de Poisson (v) = 0,29
- Limite d'élasticité = 36 000 psi
- Type non linéaire = Plastique
- Données relatives aux contraintes/déformations :
| Déformation | Contrainte - psi (kPa) |
|---|---|
| 0,0 | 0,0 |
| 0,0012 | 36,000 (248,211) |
| 0,5 | 36,000 (248,211) |
Contraintes
- Support structurel sans frottements au niveau de chacune des trois surfaces planes
Charge
- Pression transitoire appliquée à la surface sphérique intérieure
- Données de courbe multiplicateur (la pression augmente de 1 000 psi par milliseconde) :
| Durée | Magnitude |
|---|---|
| 0,0 | 0,0 |
| 0,051 | 51,000 |
Résultats théoriques
Nous envisageons des solutions pour les deux cas de limites à mesure que la plasticité progresse de la surface intérieure à la surface extérieure :
- Cas 1 (début de plasticité) dans lequel la surface intérieure devient plastique
- Cas 2 (pénétration plastique de 100 %) dans lequel la surface extérieure devient plastique
Nous calculons deux variables : le déplacement radial de la surface intérieure (δ i) en pouces et la pression appliquée (P) en psi.
Cas 1 (plastique)
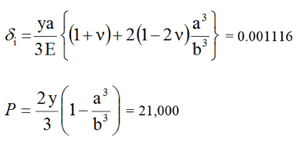
Cas 2 (plastique 100 %)
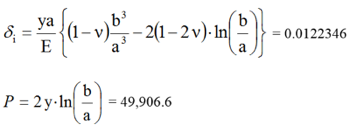
Où :
- y = 36 000 psi (limite d'élasticité du matériau)
- E = 30 x 106 psi (module de Young)
- ν = 0,29 (coefficient de Poisson)
- a = 2 po (rayon interne de la sphère)
- b = 4 po (rayon externe de la sphère)
Comparaison des résultats
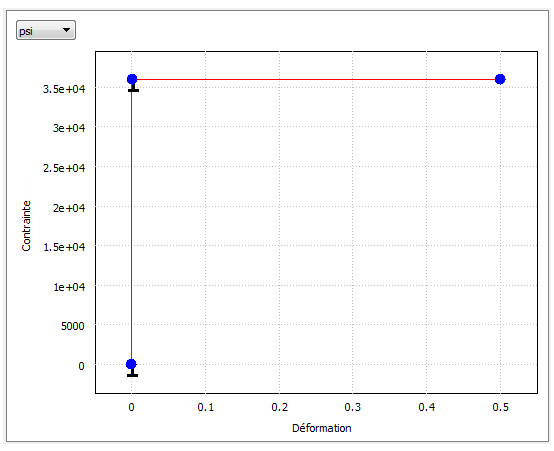
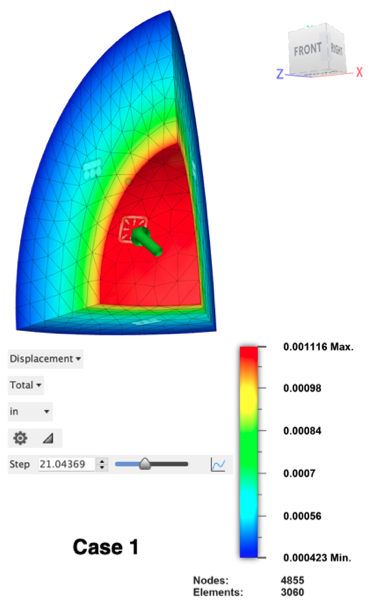
Fusion interpole les résultats entre les incréments de sortie du solveur. La pression à laquelle le modèle atteint simplement un niveau de contrainte de 36 000 psi peut être déterminée à l’aide du tableau 2D des résultats de contrainte maximale de Von Mises. Le plus proche possible, localisez le point le long du graphique où le niveau de contrainte atteint d’abord 36 000 psi. Effectuez un zoom avant pour améliorer la résolution lorsque vous faites glisser le réticule sur le graphique. Pour effectuer un zoom, cliquez sur la partie critique du graphique et faites-la glisser. L’étape Cas 1 est d’environ 21,04. La pression augmente de 1 000 psi par pas. Par conséquent, la pression appliquée pour le cas 1 = (21,04 - 1,000) * 21 040 psi = 20 940 psi.
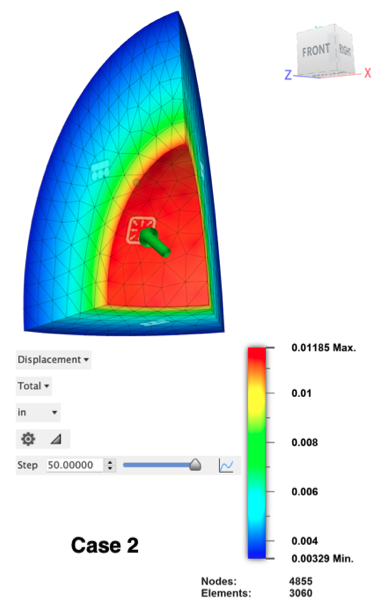
Affichez les résultats du déplacement total pour la même étape. En raison de la géométrie, tous les déplacements sont radiaux et le déplacement maximal se produit sur la surface intérieure tout au long de l'événement.
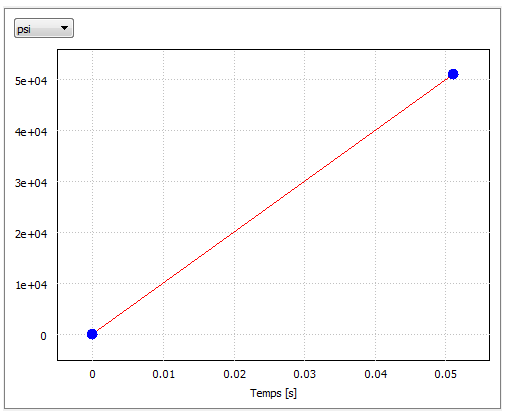
La pression à laquelle la plasticité totale est atteinte est déterminée en examinant le tableau 2D des résultats de déplacement total maximum. Déterminez le pas auquel le déplacement maximal est sur le point d'augmenter rapidement. (Une fois la plasticité totale atteinte, il n’y a rien pour empêcher l’expansion rapide de la sphère.) Cette condition se produit approximativement à l’étape 50,00. Le déplacement augmente très progressivement jusqu’à cette étape. Depuis l’étape 50,0001 vers le haut, le taux de changement est nettement augmenté. Par conséquent, la pression appliquée pour le cas 2 = 50 * 1 000 psi = 50 000 psi. La légende du tracé indique le déplacement correspondant.
| Numéro de cas | Pression appliquée (psi) : | Déplacement radial (pouces) : | ||||
|---|---|---|---|---|---|---|
| Théorie | Fusion | % de différence | Théorie | Fusion | % de différence | |
| 1 | 21,000 | 21,040 | 0,19 % | 0,001116 | 0,001116 | -0,00 % |
| 2 | 49,906.6 | 50,000 | 0,19 % | 0,0122346 | 0,01185 | -3,14 % |
Référence
Chakrabarty, J., Theory of Plasticity, McGraw-Hill, New York, 1987, pages 307-311.