Contrainte thermique 03 : validation de matériau dépendant de la température
Vérifiez la déformation mécanique et thermique à diverses températures pour une matière dépendante de la température.
Description du cas
Trois tiges circulaires identiques sont soumises à une force de tension commune de 6 000 livres avec chaque tige à une température différente : 100, 300 et 500 °F. Les tiges sont contraintes de manière à les maintenir statiquement stables, mais ne gênent pas la dilatation thermique naturelle ou la déformation de traction attendue. La zone de coupe initiale de chaque tige est de 1 pouce carré et chaque tige de 10 pouces de longueur initiale. Les propriétés de matière dépendantes de la température sont spécifiées. Le coefficient de dilatation thermique, le module de Young et la limite (limite d'élasticité et résistance ultime) varient linéairement en fonction de la température. Chaque paramètre est défini pour une plage de température allant de 0 à 600 °F. Pour plus de simplicité, toutes les propriétés sont supposées varier linéairement entre 0 et 600 °F. Par conséquent, vous pouvez déterminer les propriétés de n'importe quelle température dans cet intervalle par interpolation linéaire simple.
Les déplacements axiaux (Z) et diamétraux comprennent une combinaison d'effets de charge thermique et mécanique. Le changement théorique de longueur et de diamètre de chaque tige est calculé par rapport aux résultats de la simulation Fusion. Les faces du modèle ont été scindées pour fournir des sommets à chaque point d'intérêt. Les contrôles de points sont définis à chaque emplacement de comparaison des résultats. Plus précisément, l'élongation axiale est mesurée au niveau du centre de gravité des faces d'extrémité sur lesquelles les charges de 6 000 livres sont appliquées. De plus, le changement de diamètre est mesuré au niveau des points centraux des éléments morts supérieurs et inférieurs à l'emplacement de la mi-longueur le long de chaque tige. Dans ce cas, les déplacements Y sont utilisés pour déterminer le changement de diamètre.
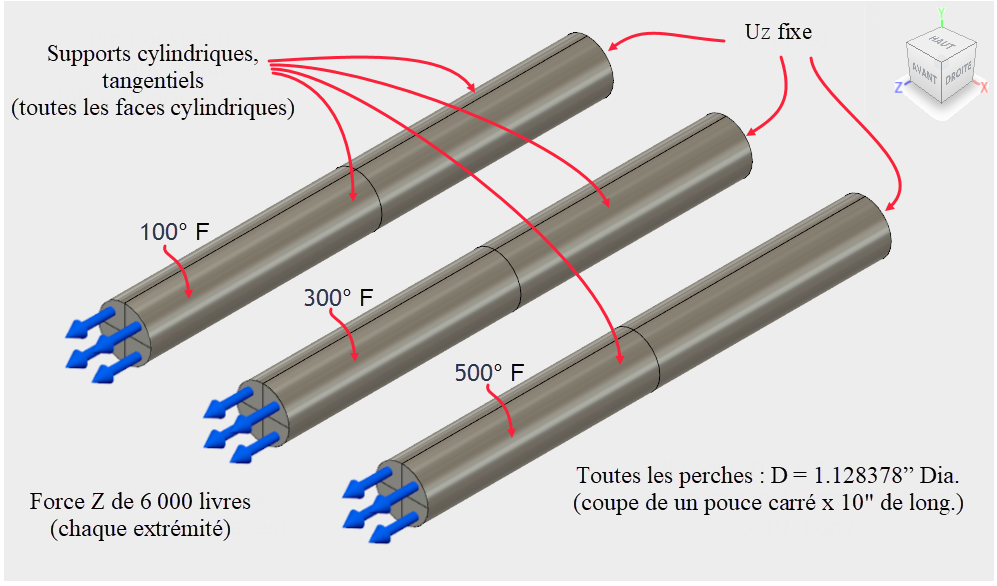
Figure 1 : diagramme du modèle
Cotes (pouce)
- Diamètre de chaque tige : 1,128378 (produit une aire de coupe de 1,000 pouce2)
- Longueur de chaque tige : 10,0
Type et paramètres de l’étude
- Type d’étude : contrainte thermique
- Température de référence sans contrainte : 0 °F
Paramètres de maillage
- Type de maillage : solide, tétraédrique
- Taille du maillage : 0,19 pouce, absolu
- Ordre d’élément : parabolique
- Créer des éléments de maillage courbés : activé
- Affinement du maillage adaptatif : aucun
Propriétés du matériau
L’image suivante représente une capture d’écran des propriétés Avancé > Dépendant de la température définies dans Fusion :
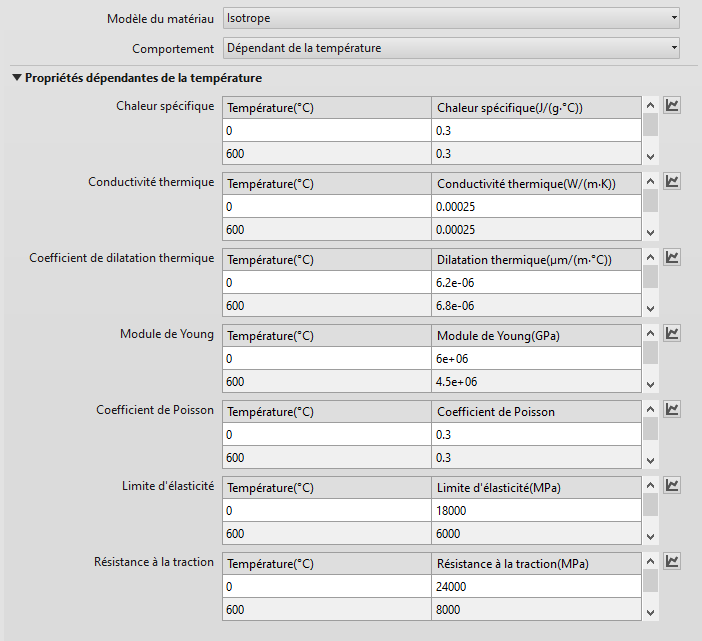
Figure 2 : propriétés des matériaux dépendantes de la température
Contraintes
- Contrainte de fixité, direction Z uniquement (UZ) : face d’extrémité circulaire -Z de chaque tige
- Contrainte de blocage, direction tangentielle uniquement : toutes les faces cylindriques de chaque tige
Charges
Structurelle
- Force, 6 000 livres dans la direction Z : sur chaque face d’extrémité +Z de chaque tige.
(Chacune de ces faces est divisée en quatre quarts. Par conséquent, le programme applique 1 500 livres/quart à une charge totale de 6 000 livres/tiges.)
Thermique
- Température appliquée, 100 °F : premier corps (tige dans la position -X)
- Température appliquée, 300 °F : deuxième corps (tige en position moyenne)
- Température appliquée, 500 °F : troisième corps (tige dans la position +X)
Solution théorique
Les variables utilisées dans les équations et le tableau sur cette page sont définies comme suit :
- δz : déplacement Z (axial). Des invites supplémentaires indiquent si l’effet est thermique (δz_t) ou dû à la force structurelle (δz_f).
- α : coefficient d’expansion thermique (varie en fonction de la température)
- T : température
- E : module de Young (varie en fonction de la température)
- ν : coefficient de Poisson
- L : longueur initiale de la tige
- D : diamètre initial de la tige
- ΔD : modification du diamètre de tige. Les indices indiquent si l’effet est thermique (ΔDt) ou dû à la force structurelle (ΔDf).
- F : force de tension axiale appliquée (6 000 livres).
- A : aire de la section transversale initiale de chaque tige (1 po2)
Pour toutes les équations, les propriétés de matériau sont interpolées linéairement entre les deux points de données spécifiés (0 °F et 600 °F). Par exemple, le module de Young (E) à 500 °F est déterminé comme suit :
E0 = 6 x 106 psi E600 = 4,5 x 106 psi E500 = E0 + (500° F / 600° F)(E600 - E0) = 6 x 106 psi + (5/6)(4,5 x 106 psi - 6 x 106 psi) = 4,75 x 106 psi
Utilisez la même technique pour toutes les propriétés de matériau, car elles sont toutes définies avec une ligne droite (pente constante) comprise entre 0 et 600 °F.
Déplacement axial
Le déplacement axial est la combinaison de la dilatation thermique due à la température appliquée et à l'élongation structurelle due à la force appliquée. Dans tous les cas, ces deux effets fonctionnent dans la même direction et sont directement additifs.
Composant thermique
δz_t = T * α * L
Composant de structure
δz_f = (F/A) / E * L
Modifier le diamètre
Composant thermique
ΔDt = T * α * D
Composant de structure
Élément ΔDf = (F/A) / E * ν * D
Comparaison des résultats
Déplacement axial
Trois contrôles de point ont été définis pour déterminer le déplacement Z au niveau du centre de gravité de la face de fin de chaque tige (+Z, extrémité libre) :
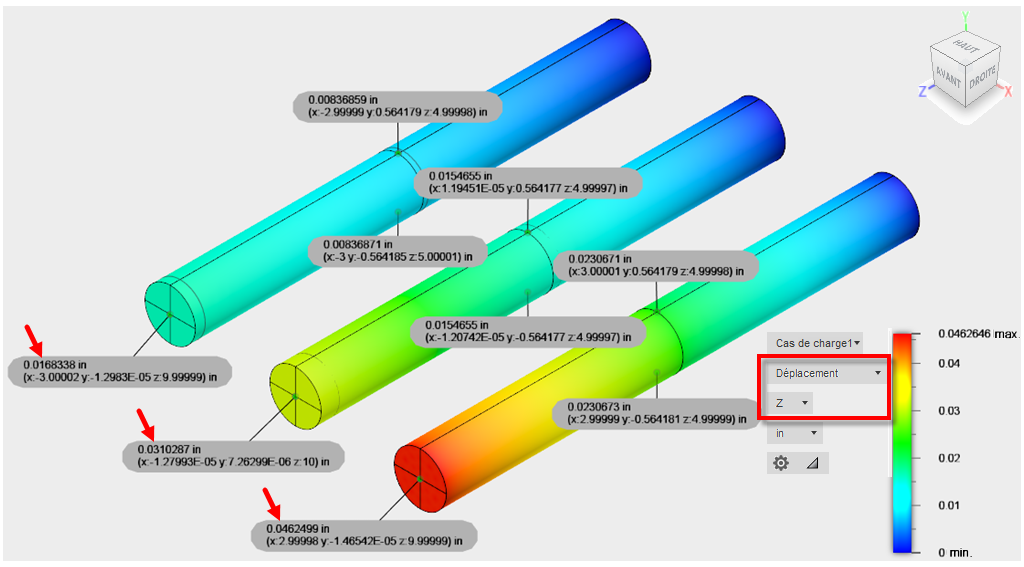
Figure 3 : résultats du déplacement Z
Modifier le diamètre
Six points de contrôle ont été définis pour déterminer le déplacement Y au niveau des points du centre mort supérieur (TDC) et du centre mort inférieur (BDC) à l'emplacement de la mi-longueur le long de chaque tige. Les valeurs combinées de déplacement Y sont égales au changement de diamètre des tiges, conformément à l'équation suivante :
ΔD = δy(TDC) - δy(BDC)
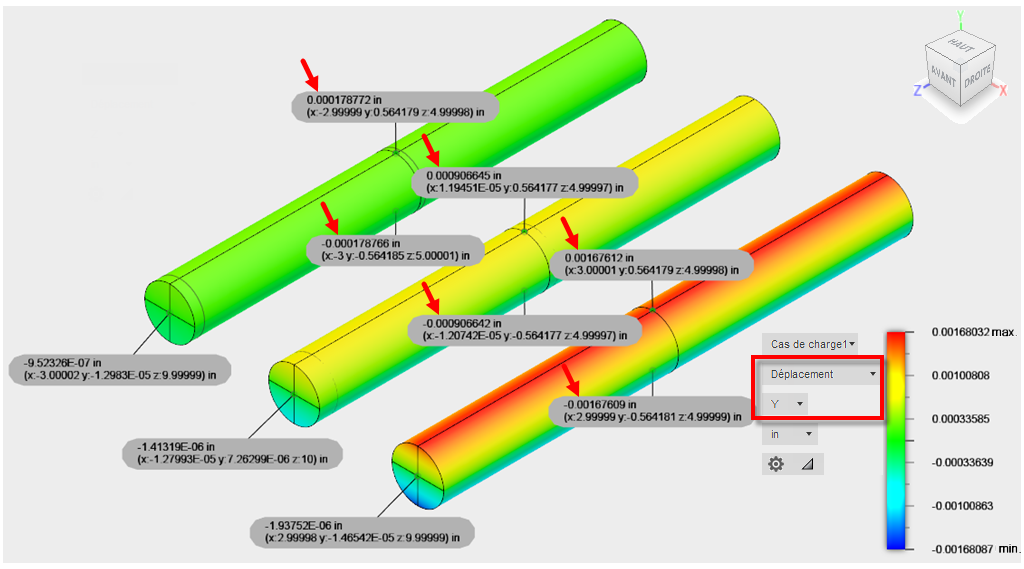
Figure 4 : résultats du déplacement Y
Tableau de comparaison des résultats
Les tableaux suivants comparent les résultats de la simulation théorique et Fusion pour le déplacement Z (élongation) et changent le diamètre des tiges aux trois températures d’essai.
| Température (° F) | Résultats théoriques (pouce) | |||||
|---|---|---|---|---|---|---|
| δz_t | δz_f | δz(Total) | ΔDt | ΔDf | ΔD(Total) | |
| 100 | 0,0063000 | 0,01043478 | 0,01673478 | 0,000710879 | -0,000353232 | 0,000357647 |
| 300 | 0,0195000 | 0,01142857 | 0,03092857 | 0,002200341 | -0,000386873 | 0,001813468 |
| 500 | 0,0335000 | 0,01263158 | 0,04613158 | 0,003780073 | -0,000427597 | 0,003352476 |
| Température (° F) | Résultats de Fusion (pouces) | Variation | ||
|---|---|---|---|---|
| δz(Total) | ΔD | δz(Total) | ΔD(Total) | |
| 100 | 0,0168338 | 0,000357538 | -0,030 % | 0,592 % |
| 300 | 0,0310287 | 0,001813287 | -0,010 % | 0,324 % |
| 500 | 0,0462499 | 0,003352210 | -0,008 % | 0,256 % |